Synopsis

Keywords: Motion Correction, Image Reconstruction

Respiratory motion is a significant challenge for the acquisition of reliable renal R₂^*/QSM. The combination of 3D multi-echo UTE cones MRI and respiratory motion-resolved image reconstruction with an image-based self-navigator was developed to enable motion-robust renal R₂^*/QSM. Motion-resolved reconstruction with an image-based self-navigator showed better image quality compared to conventional gridding reconstruction and higher apparent SNR and CNR compared to motion-resolved reconstruction using the center of the k-space as navigator. 3D multi-echo UTE cones MRI and motion-resolved image reconstruction with image-based self-navigator demonstrated the feasibility of motion-robust, free-breathing, and high isotropic resolution of renal R₂^*/QSM.

Introduction

Respiratory motion is one of the major challenges in the acquisition of reliable renal R₂^*/QSM. In this work, a combination of 3D multi-echo UTE cones MRI^1,2 and respiratory motion-resolved image reconstruction with an image-based self-navigator was developed to demonstrate the feasibility of motion-robust, free-breathing, and high isotropic resolution of renal R₂^*/QSM. The proposed method is validated on phantom and in-vivo experiments against conventional gridding reconstruction and motion-resolved reconstruction that uses the center of the k-space for navigation³.

Methods

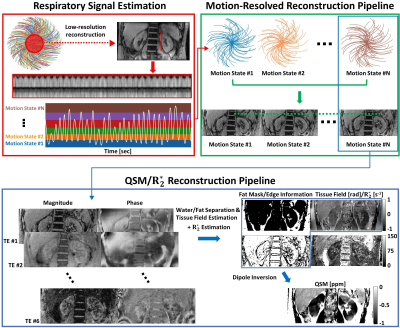
Respiratory signal estimation and image reconstruction
Using k-space data from 3D multi-echo UTE cones acquired with free-breathing, two respiratory signals were estimated. A DC-based respiratory signal was estimated as follows: First, for each echo bandpass filtering was performed on DC signals extracted from each coil. Second, SVD was performed on the filtered DC signals along the coil dimension, and the first principal component was retrieved from each echo and concatenated. Third, an additional SVD was applied to the concatenated principal components along the echo dimension. A respiratory signal from image-based self-navigator was estimated as follows: First, a low-resolution image was reconstructed using multi-scale low-rank reconstruction⁴. From the center of k-space, 35% of readout data were used to reconstruct low-resolution images. For each frame, the number of allocated cone interleaves was set to enable a temporal resolution of approximately 300ms to capture the respiratory motion. Second, a perpendicular line profile across the kidney was extracted over time to visualize respiratory motion. Third, based on concatenated line profile, the respiratory signal was estimated.
Based on the estimated respiratory signal, the cones interleaves were sorted, and compressed sensing-based motion-resolved image reconstruction with temporal total variation along the motion state dimension was performed (XD-GRASP)⁵. For comparison, conventional gridding reconstruction was performed as a motion-averaged reconstruction.

QSM reconstruction
Complex-based nonlinear least squares fitting was performed with SPURS⁶ to estimate the B0 field map. The tissue field was then estimated from LBV⁷. In the case of the phantom study (no fat), the B0 field map was estimated by mono-exponential least-squares fitting⁸ followed by region growing-based phase unwrapping. QSM was computed by solving the following inversion problem^9,10:
$$\hat{\chi}=argmin_{\chi}\frac{1}{2}\parallel\omega(e^{-i(d\ast\chi)}-e^{-if})\parallel_2^2+\lambda_{1}\parallel M_{G}\triangledown\chi\parallel_{1}+\lambda_{2}\parallel M_{fat}(\chi-\bar{\chi}_{fat})\parallel_2^2,$$
where χ is the desired susceptibility map, d is the dipole kernel in image space, f is the tissue field, ω is the noise weighting, $$$\triangledown$$$ is the gradient operator, M_G is the binary gradient mask, M_fat is the fat mask derived from PDFF>80%, λ₁ and λ₂ are regularization parameters, and $$$\bar{\chi}_{fat}$$$ is the mean susceptibility value inside the fat mask. Regularization parameters were λ₁=5×10^-3 and λ₂=0 for phantom, and λ₁=2×10^-3 and λ₂=2×10^-1 for in-vivo. Figure 1 shows our R₂^*/QSM reconstruction pipeline.

Phantom and in-vivo studies
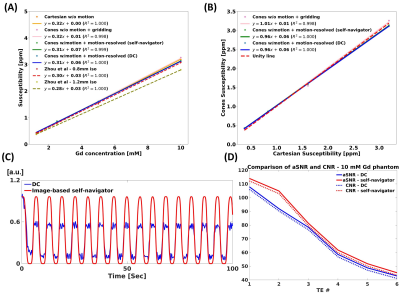
A gadolinium phantom was constructed as shown in Figure 2(C). To generate motion artifacts, periodic table motion was applied to one acquisition as shown in Figure 2(D).
With local IRB approval, one healthy volunteer was scanned. All images were acquired using a 3T clinical MRI scanner (SignaPremierXT, GE Healthcare, Waukesha, WI). For phantom, 3D Cartesian images were acquired using a chemical-shift-encoded multi-echo spoiled gradient echo sequence with the following parameters: initial TE/ΔTE/TR=1.5/0.8/7.5ms, #TEs=6, flip angle (FA)=4°, matrix size=260×260×260, in-plane resolution=1×1mm², slice thickness=1mm, receiver bandwidth (rBW)=962 Hz/Px, and scan time=25min 31s. For phantom and in-vivo, 3D multi-echo UTE cones acquisitions were performed following parameters: initial TE/ΔTE/TR=0.032(1.1)/2(3.3)/15(30)ms, #TEs=6, FA=4(12)°, matrix size=260(270)×260(270)×260(110), in-plane resolution=1(1.5)×1(1.5)mm², slice thickness=1(1.5)mm, rBW=962 Hz/Px, and scan time = 23(20)min 10(26)s.

Results

Phantom study
Motion-resolved reconstruction using a self-navigator showed comparable susceptibility map quality with Cartesian and cones without periodic table motion, while motion-averaged reconstruction showed severe motion artifacts (Figure 2(A)). Motion-resolved reconstruction using a self-navigator showed a good agreement with Cartesian, cones without table motion, and literature values¹¹ as shown in Figure 3(A). aSNR and CNR were higher in self-navigator compared to DC for all echoes (Figure 3(D)).

In-vivo study
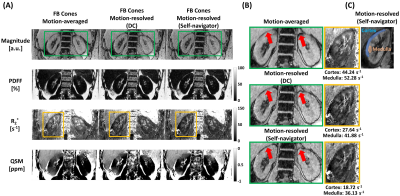
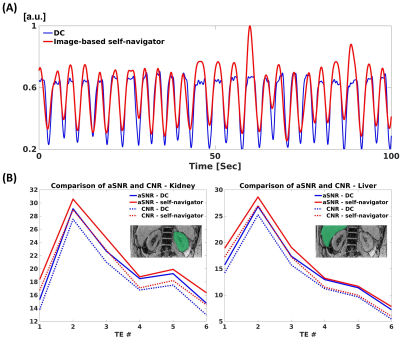
Motion-resolved reconstruction (self-navigator) showed better delineation of the kidney than motion-resolved reconstruction (DC) and motion-averaged reconstruction as marked by red arrows (Figure 4(B)). Motion-induced overestimation of R₂^* values in both cortex and medulla was decreased in the motion-resolved reconstruction using a self-navigator¹². Mean+/-std QSM values of cortex and medulla were 0.16+/-0.09 and 0.23+/-0.04 for motion-averaged, 0.08+/-0.07 and 0.17+/-0.11 for motion-resolved (DC), and -0.01+/-0.1 and 0.08+/-0.07 for motion-resolved (self-navigator), respectively. QSM values from motion-resolved reconstruction with self-navigator showed a good agreement with the literature values¹³. The self-navigator showed higher aSNR and CNR compared to the DC for all echoes as shown in Figure 5(B).

Discussion

This work demonstrated the feasibility of motion-robust, free-breathing, and high isotropic resolution renal R₂^*/QSM using a combination of 3D multi-echo UTE cones MRI and respiratory motion-resolved image reconstruction with image-based self-navigator. The utilization of 3D information in the proposed image-based self-navigators increased the performance over DC navigators, which are based on an image average¹⁴. Further optimization of imaging parameters and QSM reconstruction is required for clear delineation of the kidney cortex and medulla. A total field inversion^15,16 strategy will be investigated to reduce systematic errors in classical two-step approaches where background and local fields are deconvolved separately.

Conclusion

Free-breathing renal R₂^*/QSM with the high isotropic resolution is feasible using 3D multi-echo UTE cones MRI and motion-resolved image reconstruction with an image-based self-navigator.

Acknowledgements

No acknowledgement found.