Synopsis

Keywords: Motion Correction, Brain

‘Scout-based’ navigators exploit correlations between navigator data and a low-resolution multi-coil pre-scan data (scout) to effectively estimate either motion or B₀-perturbations. Usually, scout data has a fixed contrast, limiting their usage in estimating motion within echo-trains where contrast changes from one readout to the next (e.g. MPRAGE). Furthermore, combined motion and B₀-perturbation estimation from rapid navigators has yet to be achieved. In this work, we propose a quantitative scout (Q-SCOUT) to ‘time-resolve’ navigator contrast, along with a rapid SPINS-navigator (few ms). Q-SCOUT and rapid navigator data are used in our QUEEN method to enable within-echo-train motion and B₀-perturbation estimation.

Introduction

MRI is susceptible to motion and B₀-inhomogeneity perturbations^[1]. Navigator-based techniques have been developed to estimate and correct for these, including methods that utilize a pre-scan to guide motion/B₀ estimation. Within this class, the cloverleaf and spherical navigators^[2-3] utilize tailored k-space trajectories to sensitize signals to rigid motion. FID multi-coil navigators [4] have been augmented with a low-resolution pre-scan ‘scout’ image to enable accurate motion^[5] or B₀-perturbation^[6] estimation. Similarly, the “SAMER+guidance-lines”^[7] approach utilizes a single-contrast scout along with 4 lines of k-space acquisition from an echo-train to achieve accurate inter-echo-train motion estimation. In this work, we propose “Quantitatively-Enhanced parameter Estimation from Navigators (QUEEN)”, to provide robust combined motion and B₀-perturbation estimation for both inter- and within-echo-train correction by using a time-resolved multi-contrast scout. A short navigator of a few ms was developed and can be flexibly inserted in most sequences. QUEEN’s novel components include i) a ‘quantitative’ scout scan (Q-SCOUT), ii) time-resolved motion and B₀ estimation and iii) a tailored SPINS navigator^[8].

Methods

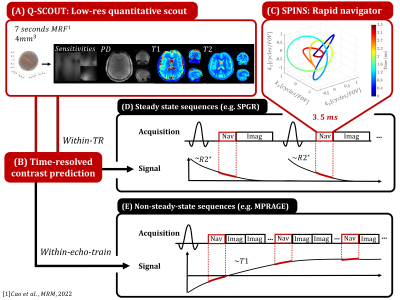
Q-SCOUT:
This work extends the concept of a single-contrast scout to a time-resolved quantitative scout (Q-SCOUT) that models the time-varying navigator signal (Fig1) to enable navigator usage in almost any sequence and/or timing. To correct for brain motion and B₀-perturbation ($$$\delta \textbf{B}_0$$$), a low-resolution Q-SCOUT is sufficient for which fast quantitative imaging sequences such as MRF and EPTI^[9,10] can be used. Fig1 showcases a 7s MRF acquisition to obtain whole-brain PD, T1, T2 and coil sensitivity information at 4mm isotropic resolution.

QUEEN:
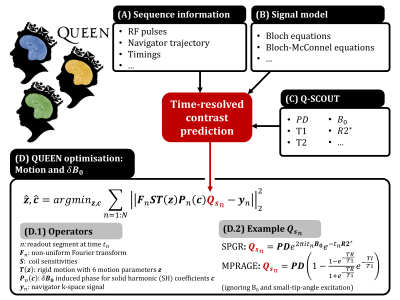
Whereas the Q-SCOUT predicts the time-varying navigator signal $$$\textbf{Q}_s(t)$$$ (Fig2), QUEEN refers to the estimation of motion and $$$\delta \textbf{B}_0$$$ parameters. Navigator k-space is modeled as a time-segmented signal:
$$
\textbf{y}_n = \textbf{F}_n\textbf{ST}(\textbf{z})\textbf{P}_n(\delta \textbf{B}_0)\textbf{Q}_{s_n}\quad\quad(1)
$$
for time-segments $$$n=1:N$$$, where $$$\textbf{F}_n$$$ is the segment-dependent non-uniform Fourier transform, $$$\textbf{P}_n$$$ the induced phase $$$e^{2\pi \delta \textbf{B}_0t_n}$$$ and $$$\textbf{Q}_{s_n}$$$ the Q-SCOUT-predicted contrast at time $$$t_n$$$. $$$\textbf{T}(\textbf{z})$$$ represents the rigid motion operator (with rigid motion parameters $$$\textbf{z}$$$) and $$$\textbf{S}$$$ contains the coil sensitivities. We model $$$\delta \textbf{B}_0$$$ using a set of 2^nd-order solid harmonics (SH) ^[11] ($$$\delta \textbf{B}_0=\textbf{Bc}$$$ with SH basis $$$\textbf{B}$$$ and coefficients $$$\textbf{c}$$$) and iteratively estimate motion and $$$\textbf{c}$$$ using the Levenberg-Marquardt algorithm:

$$
\textbf{z}^{i+1}=argmin_\textbf{z}\sum_{n=1}^{N}|| \textbf{F}_n\textbf{ST}(\textbf{z})\textbf{P}_n( \textbf{c}^{i})\textbf{Q}_{s_n}-\textbf{y}_n||^2_2\quad\quad(2)
\\\textbf{c}^{i+1}=argmin_\textbf{c}\sum_{n=1}^{N}|| \textbf{F}_n\textbf{ST}(\textbf{z}^{i+1})\textbf{P}_n( \textbf{c})\textbf{Q}_{s_n}-\textbf{y}_n||^2_2\quad\quad(3)
$$

SPINS:
The SPINS trajectory, originally designed for B1⁺-mitigated RF excitation, is used here due to its rapid acquisition and sensitivity to rigid motion and B₀ inhomogeneity: arc-sampling at multiple radii sensitizes signal to rotation and translation whilst sampling the k-space origin at start and end results in B₀ sensitivity. Acquisition time was minimized using gradient trajectory optimization^[12] (Fig1).

Simulations:
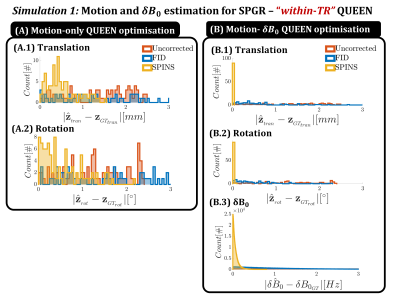
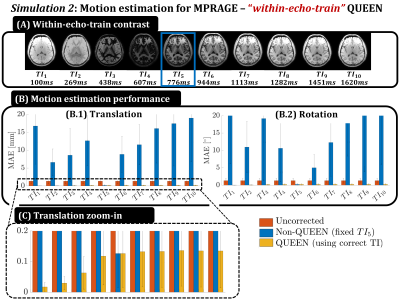
Simulation 1 compares the FID and SPINS navigator trajectory when simulating ‘within-TR’ navigator signal for an SPGR sequence (Fig2): baseline B₀- and R2*-resolved signal is simulated in the presence of motion and $$$\delta \textbf{B}_0$$$. Motion is QUEEN-estimated by either ignoring $$$\delta \textbf{B}_0$$$ (“motion-only”) or joint optimization (“motion-$$$\delta \textbf{B}_0$$$ ”). Simulation 2 simulates ‘within-echo-train’ navigator signal for MPRAGE at different inversion times (TI) (Fig3). Motion is estimated using either the correct TI (Q-SCOUT+QUEEN) or a fixed TI (fixed-SCOUT+non-QUEEN). Other effects on the signal (e.g. readout RF excitations) are ignored for simplicity but can be incorporated. B₀ can be ignored since MPRAGE usually uses short TEs, making the FID navigator preferable due to its arbitrary duration. By acquiring a 1ms FID navigator every 169ms, this simulation mimics high-temporal resolution within-echo-train motion estimation with minimal efficiency loss (0.5%).

In-vivo:
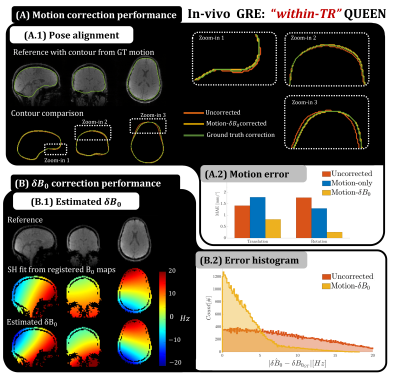
The ‘within-TR’ QUEEN was tested on a healthy volunteer by implementing the proposed SPINS in a multi-echo GRE (Fig5). Q-SCOUT data was generated at 4x4x4mm³ by retrospectively under-sampling the image acquisition and fitting B₀ and R2* maps from multi-echo images. Gradient trajectories were measured using a Skope field camera^[13]. Data was acquired in 1) a reference pose and 2) a different pose whilst placing the arms close to the head to induce B₀ variation. QUEEN was compared to the ground truth, obtained by registering reconstructed images and B₀ maps. ROVir coil compression^[14] was used to suppress signal from regions of non-rigid neck motion.

Results and discussion

Results for simulation 1 are shown in Fig3, where coupling between motion and $$$\delta \textbf{B}_0$$$ estimation is observed (3.A -B). Improved estimation is obtained for the proposed “motion-$$$\delta \textbf{B}_0$$$ ” QUEEN optimization. Furthermore, SPINS outperform the FID trajectory in the presence of $$$\delta \textbf{B}_0$$$. Results for simulation 2 (Fig4) show that the time-resolved Q-SCOUT drastically improves the QUEEN motion estimation for TIs away from the fixed-SCOUT. Even with the Q-SCOUT, slight sensitivity of parameter estimation to contrast is observed (4.B). In-vivo results (Fig5) confirm improved motion estimation for the “motion-$$$\delta \textbf{B}_0$$$” QUEEN, although with reduced accuracy compared to simulations. Observed systematic signal inconsistencies (not shown) are hypothesized to be the cause.

Conclusion

We have proposed a quantitative scout (Q-SCOUT) to predict time-resolved navigator contrast for enhanced motion and B₀-perturbation estimation (QUEEN). A rapid navigator was developed for this purpose and can be flexibly inserted in most sequences. Simulations show the potential of Q-SCOUT+QUEEN to achieve improved motion estimates, especially in the presence of B₀-perturbations. This was confirmed in-vivo, although model imperfections limit the achieved accuracy. Future work will investigate these model imperfections and translate the proposed approach to in-vivo within-echo-train motion correction.

Acknowledgements

This work was partly funded by the King’s College London & Imperial College London EPSRC Centre for Doctoral Training in Medical Imaging [EP/S022104/1].