0989

µGUIDE: a framework for microstructure imaging via generalized uncertainty-driven inference using deep learning
Maëliss Jallais1,2 and Marco Palombo1,2
1Cardiff University Brain Research Imaging Centre, Cardiff University, Cardiff, United Kingdom, 2School of Computer Science and Informatics, Cardiff University, Cardiff, United Kingdom

Synopsis

Keywords: Signal Modeling, Microstructure, dMRI

This work proposes µGUIDE: a general Bayesian framework to estimate posterior distributions of tissue microstructure parameters from any given biophysical model or MRI signal representation, with exemplar demonstration in diffusion-weighted MRI. Harnessing a new deep learning architecture for automatic signal feature selection combined with simulation-based inference and efficient sampling of the posterior distributions, µGUIDE bypasses the high computational and time cost of conventional Bayesian approaches and does not rely on acquisition constraints to define model-specific summary statistics. The obtained posterior distributions allow to highlight degeneracies present in the model definition and quantify the uncertainty and ambiguity of the estimated parameters.

Introduction

Diffusion-weighted MRI (dMRI) is a promising technique for characterizing brain microstructure in-vivo1,2,3. Traditional approaches quantify histologically meaningful features of brain microstructure by fitting a biophysical model voxel-wise to the set of signals obtained from images acquired with different sensitivities, yielding model parameter maps1. However, traditional maps only represent the best solution and do not provide confidence measures that could guide the results’ interpretation.

Posterior distributions are powerful tools to characterize all the possible parameter estimations that could explain an observed measurement, the uncertainty in those estimations, and existing model degeneracies. But the lack of tractable likelihood for most of the models makes traditional methods practically unusable4.

Conventional Bayesian inference approaches such as Markov-Chain-Monte-Carlo (MCMC) methods are computationally expensive and time consuming. More recent machine learning methods developed to accelerate posterior distribution estimation rely on the definition of summary statistics to handle the high-dimensionality of data like dMRI4,5,6. However, the summary statistics are model-specific, not easy to define and rely on specific acquisition requirements.

Harnessing a new deep learning architecture for automatic signal feature selection and efficient sampling of the posterior distributions, here we propose µGUIDE: a general Bayesian framework to estimate posterior distributions of tissue microstructure parameters from any given biophysical model/signal representation. µGUIDE extends and generalises previous work5 to any forward model and without acquisition constraints, providing fast estimations of posterior distributions voxel-wise. We demonstrate µGUIDE using numerical simulations and dMRI data from healthy human volunteers and epileptic patients.

Methods

The µGUIDE framework relies on a Simulation-Based Inference (SBI) formulation4,5, which, in the case of dMRI datasets, takes as input $$$x$$$ a multi-shell diffusion-weighted signal and outputs the posterior distributions $$$p(θ|x)$$$ of the model parameters θ in each voxel (further details in Fig.1).

The training is performed using simulation samples generated following the forward model definition, i.e. $$$x=\mathcal{M}(\theta)$$$. $$$p(θ|x)$$$ is approximated using a conditional density estimator $$$q_{Φ}(θ|x)$$$ parametrized by Φ, and is obtained by minimizing a N-sample Monte-Carlo approximation of the average Kullback-Leibler divergence w.r.t. $$$q_{Φ}(θ|x)$$$, for different choices of x: $$\min_{Φ}\mathbb{E}_{x\sim{p(x)}}\left[\mathrm{D}_{\mathrm{KL}}\left(p(\theta{\mid}x)\|q_\phi(\theta\mid x)\right)\right]\approx-\frac{1}{N}\sum_{i=1}^{N}\log{q_\phi\left(\theta_i{\mid}x_i\right)}$$

We define four measures to characterize the obtained posterior distributions: best estimate of model parameters, uncertainty, degeneracy and ambiguity (see detailed definitions in Fig.2).

We compare the posterior distributions obtained using µGUIDE and previous methods based on six manually defined summary statistics5,6. We show exemplar applications to two biophysical models from the literature:

  • The Standard Model3 (SM): a two-compartment model with neurite signal fraction f, intra-neurite diffusivity Da, orientation dispersion index ODI, and parallel/perpendicular diffusivity within the extra-neurite space De||/De┴. We use the LEMONADE6 framework to define six summary statistics.
  • An extended-SANDI model7: a three-compartment model with neurite signal fraction fn, intra-neurite diffusivity Dn, orientation dispersion index ODI, soma signal fraction fs, a proxy of soma radius and diffusivity5 Cs, and extra-cellular isotropic diffusivity De. We use the six summary statistics defined in5, which are based on a high- and low b-value signal expansion.
The training was performed on N=106 numerical simulations for each model, computed using MISST8 and random combinations of the model parameters, each uniformly sampled from physically plausible ranges. µGUIDE relies on the sbi9 and nflows packages.

We applied the method first on simulated test-sets generated similarly to the training-set, and then on real data acquired using a PGSE acquisition with b-values=[200,500,1200,2400,4000,6000]s/mm2, [20,20,30,61,61,61] uniformly distributed directions respectively, and δ/Δ=7/24ms, TE/TR=76/3200ms. Only the b≤2500s/mm2 data were used for the SM, and an extra b-shell (b-value=5000s/mm2; 61 directions) was interpolated using mapl for the extended-SANDI model when using the method5 based on summary statistics.

Results

Fig.3A showcases µGUIDE ability to highlight degeneracies in the model parameter estimation, considering a noise-free acquisition. Fig.3B presents the posterior distributions obtained on simulations by using either µGUIDE or summary statistics for Signal-to-Noise-Ratio=50. Two cases are presented, obtained mimicking white matter (WM) and grey matter (GM) tissues. Sharper and less biased posterior estimations are obtained with µGUIDE.

Fig.4 presents the parametric maps of an exemplar set of model parameters, alongside their uncertainty, degeneracy and ambiguity, obtained on real data using µGUIDE with the SM and extended-SANDI model. The full posterior distributions are also available for each voxel.

Fig.5 demonstrates µGUIDE application to an epileptic patient. Noteworthy, f estimates from SM within the epileptic lesion show low uncertainty/ambiguity hence high confidence, while ODI estimates show high uncertainty/ambiguity suggesting low confidence, cautioning the interpretation. The two model parameters also show degeneracy in different regions of the lesion.

Discussion

The reduced bias and variance in the posterior distributions estimated with µGUIDE promise to improve parameters estimation over current methods (e.g.5). µGUIDE can be easily applied to multiple models/representations and obtain faster posterior distributions estimations. Constraints imposed by the definition of the manually-defined summary statistics are removed, but µGUIDE is still a model-dependant method (e.g., training is model-based).

µGUIDE allows to highlight degeneracy and obtain information about the uncertainty and ambiguity of an estimation, guiding results interpretation. As demonstrated by our pathologic example, changes of those measures can help clinicians decide which parameters are the most reliable and better interpret microstructure changes within diseased tissue.

Conclusion

For any given acquisition and signal model/representation, µGUIDE improves parameters estimation and allows to highlight existing degeneracies, and quantify uncertainty and ambiguity.

Acknowledgements

This work, MJ and MP are supported by UKRI Future Leaders Fellowship (MR/T020296/2).

We are thankful to Dr. Dmitri Sastin and Dr. Khalid Hamandi for sharing their dataset from epileptic patient.

References

  1. Alexander, DC, Dyrby, TB, Nilsson, M, Zhang, H. Imaging brain microstructure with diffusion MRI: practicality and applications. NMR in Biomedicine. 2019.
  2. Jelescu IO, Palombo M, Bagnato F, Schilling KG. Challenges for biophysical modeling of microstructure. J Neurosci Methods. 2020.
  3. Novikov, DS, Fieremans, E, Jespersen, SN, Kiselev, VG. Quantifying brain microstructure with diffusion MRI: Theory and parameter estimation. NMR in Biomedicine. 2019.
  4. Cranmer K, Brehmer J, Louppe G. The frontier of simulation-based inference. Proc National Acad Sci. 2020.
  5. Jallais, M., Rodrigues, P.L.C., Gramfort, A. and Wassermann, D. Inverting brain grey matter models with likelihood-free inference: a tool for trustable cytoarchitecture measurement. Machine Learning for Biomedical Imaging. 2022.
  6. Novikov DS, Veraart J, Jelescu IO, Fieremans E. Rotationally-invariant mapping of scalar and orientational metrics of neuronal microstructure with diffusion MRI. Neuroimage. 2018.
  7. Palombo, M., Ianus, A., Guerreri, M. Nunes, D., Alexander, D.C., Shemesh, N., Zhang, H. SANDI: A compartment-based model for non-invasive apparent soma and neurite imaging by diffusion MRI. NeuroImage. 2020.
  8. Ianuş, A., Shemesh, N., Alexander, D.C. and Drobnjak, I. Double oscillating diffusion encoding and sensitivity to microscopic anisotropy. Magn. Reson. Med. 2017.
  9. Tejero-Cantero A, Boelts J, Deistler M, Lueckmann J-M, Durkan C, et al. sbi: A toolkit for simulation-based inference. J Open Source Softw. 2020.
  10. Papamakarios, G., Nalisnick, E.T., Rezende, D.J., Mohamed, S., and Lakshminarayanan, B. Normalizing ows for probabilistic modeling and inference. JMLR. 2021.
  11. Germain, M., Gregor, K., Murray, I., Larochelle, H. Made: Masked autoencoder for distribution estimation. In Proceedings of the 32nd International Conference on Machine Learning. 2015.

Figures

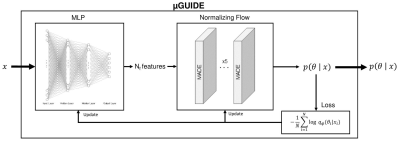
µGUIDE architecture. Input: an observed signal. Output: a posterior distribution of the parameters. Based on a SBI4,5 framework, it combines a Multi-Layer Perceptron (MLP) with 3 layers and a Normalizing Flow11, composed of 5 stacked MADEs12. The MLP learns a low-dimensional representation of x, based on a small number of features (Nf), that can be either defined a priori or determined empirically during training. The MLP is trained simultaneously with the NF, leading to the extraction of the optimal features that minimize the uncertainty of $$$p(θ|x)$$$, i.e. uncertainty-driven.

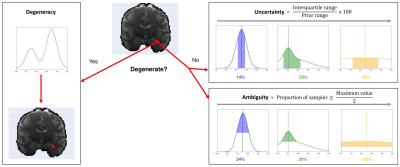
Presentation of the three measures introduced to quantify a posterior distribution on exemplar posterior distributions. Maximum A Posteriori (MAP): is the most likely parameter estimate (dashed vertical lines). Degeneracy: highlights the presence of multiple possible parameter solutions in a voxel. Uncertainty: measures the dispersion of the 50% most probable samples using the interquartile range, with respect to the prior range. Ambiguity: measures the Full Width at Half Maximum (FWHM), in percentage with respect to the prior range.

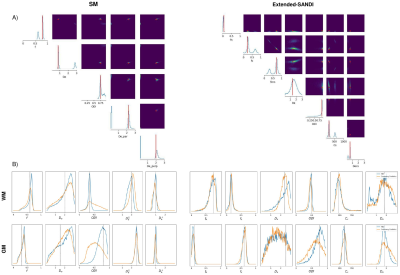
Simulation results. A) Posterior distributions (diagonal) and joint posterior distributions (upper diagonal) of microstructure parameters for the SM and extended-SANDI model, using MLP-extracted features (SNR=$$$\infty$$$). µGUIDE allows to highlight degeneracies present in the model definition. B) Posterior distributions of microstructure parameters for both models using µGUIDE (blue) or manually-defined summary statistics5,6 (orange) (SNR=50). The new framework using the MLP allows to reduce the bias and variance of the obtained posterior distributions.

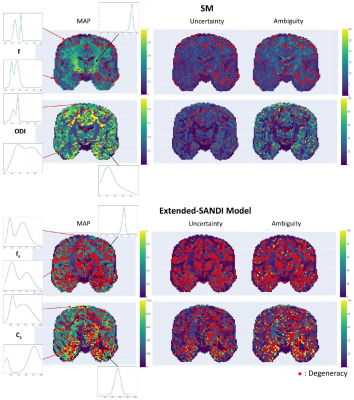
Parametric maps of the SM (top) and extended-SANDI model (bottom), obtained using the µGUIDE framework: maximum a posteriori estimation (MAP), uncertainty and ambiguity measures, overlayed with voxels considered degenerate (red dots).

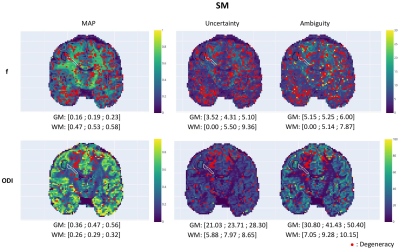
Parametric maps of an epileptic patient obtained using the µGUIDE framework with the SM, superimposed with the GM (black) and WM (white) lesions segmentation. First quartile, mean value and third quartile of the MAP, uncertainty and ambiguity measures are reported in the two ROIs. Lower MAP values are obtained in the lesions for the neurite proportion f and the ODI compared to healthy tissue. Higher uncertainty and ambiguity ODI values are reported, suggesting less stable estimations.

Proc. Intl. Soc. Mag. Reson. Med. 31 (2023)
0989
DOI: https://doi.org/10.58530/2023/0989