Synopsis

Keywords: Machine Learning/Artificial Intelligence, Image Reconstruction

Deep learning-based image reconstruction has two known practical issues: (a) sensitivity to data perturbations, and (b) poor generalization. An approach to addressing these issues is to use classical signal models to assist/constrain deep learning. This paper performs a systematic analysis of the role of signal models in model-assisted deep learning-based reconstruction. Our results show that signal models (e.g., subspace model or sparse model) can substantially reduce the sensitivity of deep learning-based reconstruction to data perturbations; they can also help improve generalization capability.

Introduction

Deep learning (DL)-based image reconstruction methods have achieved impressive performance in many image reconstruction applications¹. However, DL-based image reconstruction has two known practical issues^2,3: (a) sensitivity to data perturbations (e.g., change in data sampling scheme), and (b) poor generalization (e.g., novel image features). An approach to addressing these issues is to use classical signal models to assist/constrain DL^4-7. A number of relevant questions arise, which include:
1) Does the model improve the robustness to changes in data acquisition parameters?
2) Does the model help reduce dependence on the selection of training data?
3) Does the model improve the reconstruction performance on unseen subject-specific novel features?
4) Can the model help assess the performance of DL-based reconstruction?

This paper performs a systematic analysis of the role of signal models in model-assisted DL-based reconstruction. We used two classical signal models: subspace model and sparse model as examples to address the above questions. Our results show that signal models especially the subspace model can substantially reduce the sensitivity of DL-based reconstruction to data perturbations; they can also help improve generalization capability especially with limited training data and/or novel image features. We also demonstrated the potential of using signal models for performance assessment.

Methods

Conventional DL-based image reconstruction methods use training data to learn an end-to-end nonlinear mapping from degraded images (or limited k-space data) to desired images^8,9. Such an approach is appropriate when large amount of training data are available based on the universal approximation theorem¹⁰. However, many imaging applications only have small amount of training data, leading to two major problems for conventional DL-based image reconstruction: (a) sensitivity to data perturbations, and (b) poor generalization.

One strategy to address the above problems is combining DL with traditional signal models. There are two main approaches: a) DL-assisted model-based reconstruction (such as ADMM net¹¹ etc), and b) model-assisted DL-based reconstruction (such as, subspace or sparse model assisted DL-based reconstruction^4-7). The former emphasizes the role of the model and to a large extent, still belongs to the class of classical model-based reconstruction methods except for the use of DL for model optimization (e.g., with a learned regularization functional). The latter emphasizes the role of DL with the model serving as an “assistant”. This work focused on analyzing the role of the signal models in this class of DL-based reconstruction methods. We chose two popular signal models: the sparse and subspace model, and one popular end-to-end variational network (E2E-VN)¹², for our study. More specifically, the end-to-end network was trained to provide the following mapping relationship:
$$\hat{\rho}(x)=f_{\text{nn}}(\rho_{m}(x)),\ \ \ \ \ \ \ \ \ \ (1)$$
where $$$\rho_{m}(x)$$$ and $$$\hat{\rho}(x)$$$ represent the network input and output, respectively. In conventional DL-based reconstruction, $$$\rho_{m}(x)$$$ is often the degraded image (say, zero-padded Fourier reconstruction). In model-assisted DL-based reconstruction, $$$\rho_{m}(x)$$$ is the initial reconstruction from a model. Specifically, in sparse model-assisted DL, $$$\rho_{m}(x)$$$ is obtained as:
$$\hat{\rho}_{m}=\text{arg}\min_{\rho_{m}}||d-E\rho_{m}||_2^2+\lambda||W\rho_{m}||_1,\ \ \ \ \ \ \ (2)$$
where $$$d$$$, $$$E$$$, $$$W$$$ represent the measurement, encoding operator and sparse transformation, respectively.
In subspace model-assisted DL, $$$\rho_{m}(x)$$$ is obtained by⁴:
$$\hat{\rho}_{m}=\sum_{r=1}^Ra_{r}\phi_{r}(x),\ \ \ \ (3)$$
with $$\left\{\hat{a}_{r}\right\}=\text{arg}\min_{\left\{a_{r}\right\}}||d-E(\sum_{r=1}^Ra_{r}\phi_{r}(x))||_2^2-\sigma^2\text{log}(p(\left\{a_{r}\right\})),\ \ \ \ \ \ \ (4)$$
where $$$\phi_{r}(x)$$$ is the pre-learned basis functions (obtained, for example, by principal component analysis of the training images), $$$a_{r}\sim p(\left\{a_{r}\right\})$$$ the corresponding coefficients and $$$\sigma^2$$$ the variance of the measure noise.

Results and Discussion

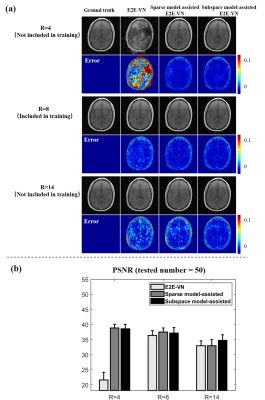
We have systematically investigated the role of signal models in model-assisted DL-based image reconstruction in improving robustness and generalization capability using the experimental data from the fastMRI dataset¹³. A couple of key points are summarized here.

First, signal models can substantially enhance the stability of DL-based reconstructions with respect to changes in data acquisition parameters and selection of training data. A couple of representative results are shown in Figs. 1-2. The improved stability comes from the fact that model-based reconstruction can naturally account for data acquisition changes through the forward operator and incorporate image priors through constrained models, thus providing a built-in “filtering” function to reduce “nuisance” signal variations induced by changes in data acquisition parameters and selection of training data.

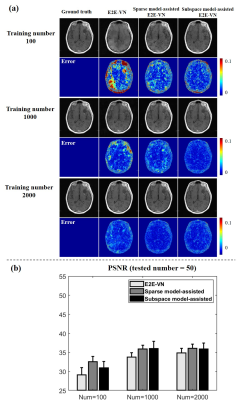
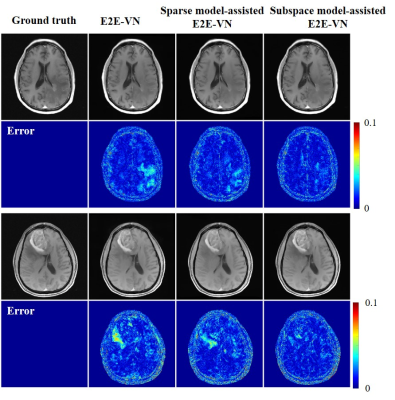
Second, signal models can help improve generalization capability. A couple of examples are shown in Figs. 3-4. The enhanced generalization capability is a result of both dimension reduction and effective representation of novel features through the signal models. More specifically, subspace model or sparse model represents the desired image function in a much lower-dimensional space through low-rank or sparse modelling. Therefore, they substantially reduce the dimensionality of the underlying learning problem, thus reducing the dependence on training data and helping recover novel features from limited data.

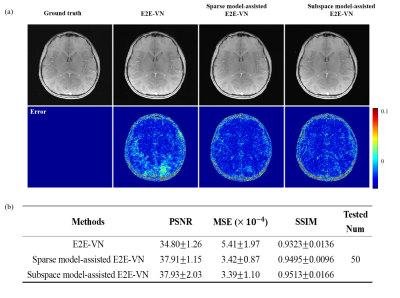
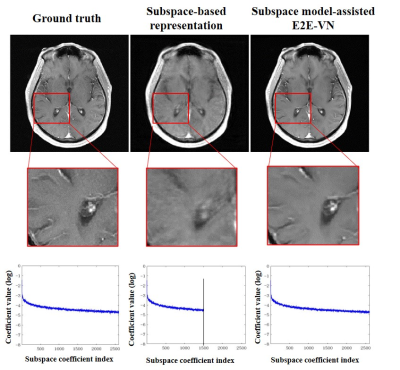
We also found that classical signal models can help assess the DL reconstruction performance by examining the subspace extrapolation effect of DL processing, illustrated in Fig. 5.

Conclusions

This paper performs a systematic analysis of the role of signal models in model-assisted DL-based reconstruction. Our results show that signal models can improve both the robustness and generalization capability of DL-based reconstruction. This work may provide useful insights into developing new methods to more effectively integrate classical signal models with DL for image reconstruction from limited data.

Acknowledgements

This work was supported by Shanghai Pilot Program for Basic Research—Shanghai Jiao Tong University (21TQ1400203); the National Natural Science Foundation of China (81871083, 62001293); and Key Program of Multidisciplinary Cross Research Foundation of Shanghai Jiao Tong University (YG2021ZD28).