0982
Physics-informed Deep Diffusion MRI Reconstruction: Break the Data Bottleneck in Artificial Intelligence1Department of Electronic Science, Biomedical Intelligent Cloud R&D Center, Fujian Provincial Key Laboratory of Plasma and Magnetic Resonance, National Institute for Data Science in Health and Medicine, Xiamen University, Xiamen, China, 2Department of Radiology, Zhongshan Hospital of Xiamen University, School of Medicine, Xiamen University, Xiamen, China, 3United Imaging Healthcare, Shanghai, China, 4Philips, Beijing, China, 5School of Computer and Information Engineering, Xiamen University of Technology, Xiamen, China
Synopsis
Keywords: Machine Learning/Artificial Intelligence, Brain, Diffusion MR, Physics-informed
Deep learning is widely employed in biomedical magnetic resonance image (MRI) reconstructions. However, accurate training data are unavailable in multi-shot interleaved echo planer imaging (Ms-iEPI) diffusion MRI (DWI) due to inter-shot motion. In this work, we propose a Physics-Informed Deep DWI reconstruction method (PIDD). For Ms-iEPI DWI data synthesis, a simplified physical motion model for motion-induced phase synthesis is proposed. Then, lots of synthetic phases are combined with a few real data to generate efficient training data. Extensive results show that, PIDD trained on synthetic data enables sub-second, ultra-fast, high-quality, and robust reconstruction with different b-values and undersampling patterns.Purpose
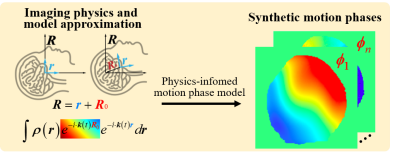
In the deep learning based Ms-iEPI DWI reconstruction, accurate training labels are unavailable due to inter-shot motion artifacts [1] caused by phase variations between shots. To overcome this bottleneck, reconstruction results of traditional optimization-based methods are employed as labels for network training [2, 3]. However, the quality of training dataset is limited by the traditional methods. Moreover, in high b-values (3000 s/mm2) and undersampling DWI, it is hard for traditional methods to provide high-quality reconstruction results [4, 5]. In this work, inspired by IPADS [6], we propose a physics-informed deep diffusion MRI reconstruction method (PIDD) to overcome the data bottleneck in the deep learning reconstruction of Ms-iEPI DWI (Figure 1).Methods
The proposed PIDD contains two main components: The multi-shot DWI data synthesis and a deep learning reconstruction network.1) The multi-shot DWI data synthesis
In brain imaging, the relative motion between scanner and brain could be simplified as shifts and rotations, because the brain motion during scanning can be approximated as a rigid body motion model [1]. Thus, the motion phase could be represented as a polynomial [7]:
$$\pmb{\phi}_j(x,y)=exp({i \cdot \sum_{l=0}^{L} \sum_{m=0}^{l}(A_{lm}x^my^{l-m})})$$
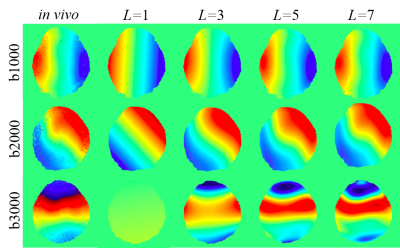
where (x, y) is the coordinates, i represents the imaginary, L is the order of the polynomial, and Alm is the coefficient of the xmyl-m. The motion phase model is employed to fit the in vivo motion phases of the multi-shot DWI images with different b-values (Figure 2). The larger L shows a better fitting ability for the complex shot phase. L=7 is selected for the balance of computational complexity and accuracy in the following motion phase generation. The whole multi-shot DWI data synthesis process is as follows: (1) Reconstruct complex B0 images (b-value = 0 s/mm2) with background phase. (2) Multiply these complex images with coil sensitivity maps that are estimated from real multi-channel k-space by ESPIRIT [8]. (3) Multiply each channel image with the synthetic motion phases to get each shot data. (4) Transform each shot image of each channel into k-space and then add Gaussian noise.
2) Deep learning reconstruction network
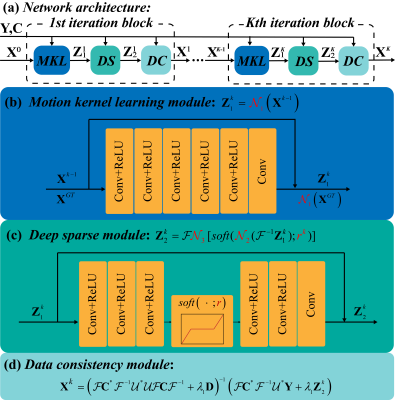
We design a reconstruction network with five blocks (Figure 3), and each block has three modules. The first module is motion kernel estimation module, which exploits the smoothness property of each shot image phase as learnable convolution kernels in the k-space. The second module is deep sparse module, which use an encoder and decoder architecture to constrain the sparsity of images in the image domain [9]. The last module is a data consistency module sloved by conjugate gradient algorithm.
Results
The 144 B0 images are acquired from 6 subjects by the 4-shot DWI sequence at a 3.0 T MRI (Philips, Ingenia CX) with 32 coils. For each B0 image, 10 motion phases are generated according to Eq. (1). The synthetic dataset contains 1440 images: 1200 synthesized from five subjects are for training and validation, and 240 from the last subject are for testing. The reconstruction network trained on this synthetic datasets is abbreviated as PIDD. PIDD is tested on both synthetic and in vivo data.1) Comparison study on synthetic data
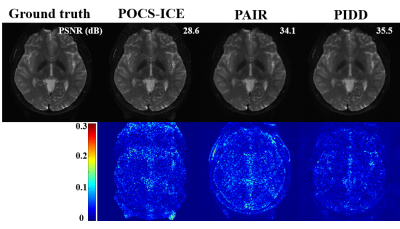
Figure 4 shows that, compared with state-of-the-art optimization-based methods POCS-ICE [10] and PAIR [4], the proposed PIDD has better PSNR [11], indicating its good noise suppression ability. Moreover, PIDD (0.1 second/slice) has much faster reconstruction speed than POCS-ICE (19.0 seconds/slice), and PAIR (40.2 seconds/slice).
2) Generalization study on multi b-value in vivo data
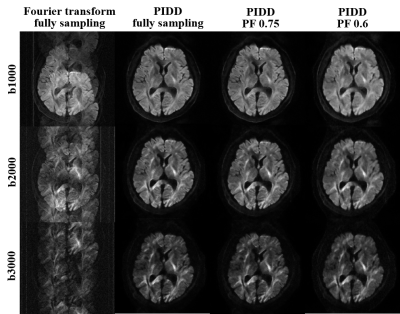
The proposed PIDD is also tested on a 3.0T in vivo 4-shot DWI dataset (United Imaging, uMR 790): resolution is 1.4 × 1.4 × 5 mm3, matrix size is 160 × 160, the channel number is 17, diffusion direction is 3, and b-values are 1000, 2000, and 3000 s/mm2. Retrospective partial Fourier sampling with sampling rates of 0.75 and 0.6 are employed in the training and testing of PIDD, respectively. Figure 5 shows that, PIDD trained on synthetic data generalizes well on the reconstruction of in vivo brain data with different b-values and undersampling patterns.
Conclusion
In this work, we demonstrate that the deep network training for DWI reconstruction can be achieved using synthetic data. The proposed PIDD overcomes the data bottleneck of deep learning methods, and enables sub-second ultra-fast reconstruction. PIDD shows promising generalization on in vivo brain data with different b-values and undersampling patterns.Acknowledgements
See more details in the full-length preprint: https://arxiv.org/abs/2210.11388. This work is supported in part by the National Natural Science Foundation of China under grants 62122064, 61971361, and 61871341, the National Key R&D Program of China under grant 2017YFC0108703, Natural Science Foundation of Fujian Province of China under grants 2021J011184, President Fund of Xiamen University under grant 0621ZK1035, and Xiamen University Nanqiang Outstanding Talents Program.
The corresponding author is Xiaobo Qu (Email: quxiaobo@xmu.edu.cn).
References
[1] A. W. Anderson, and J. C. Gore, “Analysis and correction of motion artifacts in diffusion weighted imaging,” Magn. Reson. Med., vol. 32, no. 3, pp. 379-87, 1994.
[2] H. K. Aggarwal, M. P. Mani, and M. Jacob, “MoDL-MUSSELS: Model-based deep learning for multi-shot sensitivity-encoded diffusion MRI," IEEE Trans. Med. Imaging, vol. 39, no. 4, pp. 1268-1277, 2019.
[3] Y. Hu et al., “RUN-UP: Accelerated multi-shot diffusion-weighted MRI reconstruction using an unrolled network with U-Net as priors,” Magn. Reson. Med., vol: 85, pp. 709-720, 2020.
[4] C. Qian et al., “A paired phase and magnitude reconstruction for advanced diffusion-weighted imaging,” arXiv:2203.14559, 2022. [5] Y. Huang et al., “Phase-constrained reconstruction of high-resolution multi-shot diffusion weighted image,” J. Magn. Reson., vol. 312, p. 106690, 2020.
[6] Q. Yang, Z. Wang, K. Guo, C. Cai, and X. Qu, “Physics-driven synthetic data learning for biomedical magnetic resonance: The imaging physics-based data synthesis paradigm for artificial intelligence,” IEEE Signal Process. Mag., DOI: 10.1109/MSP.2022.3183809, 2022.
[7] C. Qian et al., “Physics-informed deep diffusion MRI reconstruction: break the bottleneck of training data in artificial intelligence,” arXiv: 2210.11388, 2022.
[8] M. Uecker et al., “ESPIRiT-an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA,” Magn. Reson. Med., vol. 71, no. 3, pp. 990-1001, 2014.
[9] Z. Wang et al., “One-dimensional deep low-rank and sparse network for accelerated MRI,” IEEE Trans. Med. Imaging, DOI:10.1109/TMI.2022.3203312, 2022.
[10] H. Guo et al., “POCS-enhanced inherent correction of motion-induced phase errors (POCS‐ICE) for high-resolution multi-shot diffusion MRI,” Magn. Reson. Med., vol. 75, no. 1, pp. 169-180, 2016.
[11] Q. Huynh-Thu, and M. Ghanbari, “Scope of validity of PSNR in image/video quality assessment,” Electron. Lett., vol. 44, no. 13, pp. 800-801, 2008.
Figures