0978

A piecewise-polynomial basis for generalized diffusion encoding gradient waveforms
Emmanuel Caruyer1
1IRISA UMR 6074, Empenn ERL 1228, Univ Rennes, CNRS, Inria, Inserm, Rennes, France

Synopsis

Keywords: Diffusion/other diffusion imaging techniques, Data Acquisition

Diffusion-encoding gradient waveforms are a key parameter of experimental design in diffusion magnetic resonance imaging. Their optimization is important for e.g. maximizing the efficiency in B-tensor encoding, or improving the sensitivity and specificity to microstructure parameters of biophysical models. The main challenge in optimizing gradient waveforms and trajectories is the large dimension of the search space and the constraints associated with physical and physiological limitations. Here we propose an original piecewise polynomial representation, which natively enforces the linear constraints that arise from refocusing and regularity. We illustrate the basis on B-tensor encoding and Monte-Carlo simulation of the diffusion signal.

Introduction

Gradient waveforms in diffusion MRI play a central role to encode diffusion properties in the spin-echo signal attenuation. As a generalization to the pulsed gradient proposed in the seminal work of Stejskal and Tanner1, several studies have shown the interest to re-design the time-varying encoding gradient $$$\mathbf{g}(t)$$$. The motivation to change the gradient waveform can be practical, e.g. for the reduction of eddy-currents induced distortions2; this is also essential to probe particular microstructural properties with diffusion MRI. In biophysical modeling, the gradient waveforms6,8 and trajectories7 can be optimized to increase the sensitivity to microstructure parameters of interest. For q-space trajectory imaging with B-tensor encoding, the efficiency of the gradient trajectories can be optimized, to obtain the maximum diffusion ponderation in a given echo time3-5, with mitigation of the gradient duty cycle and concomitant (Maxwell) gradients.


Optimizing gradients is complex due to the infinite dimension of the space of admissible gradient waveforms. Besides, working with a discrete representation of the gradient usually requires interpolation when using the gradient for simulation or implementation in an MRI pulse sequence, which may introduce errors (partial refocusing or gradient slewrate overflow). To overcome some of these limitations, some studies have introduced continuous representations, either based on polynomials9 or sines and cosines12.


In this work, we propose a piecewise polynomial representation, which natively embeds the gradient waveforms requirements that can be expressed as linear constraints. We illustrate the usefulness of this compact representations for B-tensor encoding and for Monte-Carlo simulations.

Methods

We created a family of $K$ functions $$$f_k(t), t \in [0, TE]$$$, in order to represent the x-, y- and z-components of $$$\mathbf{q}(t) = \gamma \int_0^t \mathbf{g}(t')\mathrm{d}t'$$$. The functions are defined as piecewise polynomials in $$$N$$$ intervals $$$[t_n, t_{n+1}]$$$ (such that $$$t_0 = 0$$$ and $$$t_N = TE$$$). We used scaled and shifted Bernstein polynomials up to order $$$d$$$ as building blocks for these functions, for the convenient relationship they offer between values (and derivatives) at both ends of the intervals and the coefficients.

A number of constraints can be directly transcribed into linear constraints on the Bernstein coefficients in every interval:
  • $$$q(0) = q(TE) = 0$$$
  • $$$g(0) = g(TE/2 - \delta_{RF}/2) = g(TE/2 + \delta_{RF}/2) = g(TE) = 0$$$
  • $$$g(t) = 0, \forall t \in [TE/2 - \delta_{RF}/2, TE/2 + \delta_{RF}/2]$$$
  • $$$q(t)$$$ and $$$g(t)$$$ are continuous at each node $$$t_n$$$
  • the gradient is symmetric: $$$g(TE/2 - t) = - g(TE/2 + t)$$$.
Once solved, these constraints give a family of functions; we orthogonalize them for the dot product $$$\langle f,g\rangle = \int_0^{TE} f(t) g(t) \mathrm{d}t$$$ so that we obtain an orthonormal basis of functions.

Use case scenario 1: B-tensor encoding
Unlike for linear encoding, optimizing the waveforms for spherical or planar B-tensor encoding is non-trivial since some orthogonality constraints need to be respected between gradient components. The B-tensor is defined13 as $$$\mathbf{B} = \int_0^{TE}\mathbf{q}(t)\mathbf{q}(t)^\mathrm{T}\mathrm{d}t$$$. When the components $$$q_j, j\in\{\mathrm{x}, \mathrm{y}, \mathrm{z}\}$$$ are represented our orthogonal basis with coefficients $$$a_{j,k}$$$, the B-tensor simply rewrites as $$$B_{i,j} = \sum_k a_{i,k}a_{j,k} $$$. The problem of finding a gradient trajectory with maximized b-value (trace of the B_matrix) consists in solving a constrained optimization problem with a simple cost function.

Use case scenario 2: Monte-Carlo simulations
Monte-Carlo simulations is one of the methods of choice in order to study the diffusion signal in complex geometries. By observing that the accumulated phase for each spin is linear with the gradient waveform10, we have an efficient method to generate the signal for any gradient trajectory, once the phase accumulated was computed for the basis functions.

Results

We report on Fig. 1 the basis generated for piecewise constant functions, with linear transitions between ramps. This illustrates that the framework is general and naturally encompasses pulsed gradients. We also report a piecewise polynomial basis, with $$$N=7$$$ chunks and maximum order $$$d = 4$$$. The original number of degrees of freedom is 35, but this reduces to 5 once all linear constraints reported above are fulfilled.

Next, we show how the gradient trajectories can be optimized to obtain the maximum b-value for a spherical B-tensor encoding; this is compared to the original method using discrete representation4.

Last, we demonstrate the use of the framework in the context of Monte-Carlo simulation in a complex geometry, modeling a brain cell14,15. In particular, we searched for gradient trajectories with matched spherical B-tensor and $$$b=3$$$ms/µm$$$^2$$$ minimizing (resp. maximizing) the diffusion signal. This paves the way to the design of family of gradients specialized to certain geometries.

Discussion and conclusion

We introduced a piecewise polynomial function basis for the representation of the diffusion-encoding gradient waveforms. The basis is useful since it provides a continuous representation and naturally encodes common constraints on the waveforms. Two applications of the basis are illustrated, for the constrained optimization of gradient waveforms. First to find efficient waveforms for B-tensor encoding; second, to obtain new and specific contrast for a given cell geometry. We think that this framework, with the low dimension representation of gradient trajectories it offers, opens new possibilities to the complex problem of gradient waveforms optimization.

Acknowledgements

No acknowledgement found.

References

  1. Tanner, J. E., & Stejskal, E. O. (1968). Restricted self‐diffusion of protons in colloidal systems by the pulsed‐gradient, spin‐echo method. The Journal of Chemical Physics, 49(4), 1768-1777.
  2. Alexander, A. L., Tsuruda, J. S., & Parker, D. L. (1997). Elimination of eddy current artifacts in diffusion‐weighted echo‐planar images: the use of bipolar gradients. Magnetic Resonance in Medicine, 38(6), 1016-1021.
  3. Szczepankiewicz, F., Sjölund, J., Dall’Armellina, E., Plein, S., Schneider, J. E., Teh, I., & Westin, C. F. (2021). Motion‐compensated gradient waveforms for tensor‐valued diffusion encoding by constrained numerical optimization. Magnetic resonance in medicine, 85(4), 2117-2126.
  4. Sjölund, J., Szczepankiewicz, F., Nilsson, M., Topgaard, D., Westin, C. F., & Knutsson, H. (2015). Constrained optimization of gradient waveforms for generalized diffusion encoding. Journal of magnetic resonance, 261, 157-168.
  5. Szczepankiewicz, F., & Sjölund, J. (2021). Cross-term-compensated gradient waveform design for tensor-valued diffusion MRI. Journal of Magnetic Resonance, 328, 106991.
  6. Drobnjak, I., Siow, B., & Alexander, D. C. (2010). Optimizing gradient waveforms for microstructure sensitivity in diffusion-weighted MR. Journal of Magnetic Resonance, 206(1), 41-51.
  7. Drobnjak, I., & Alexander, D. C. (2011). Optimising time-varying gradient orientation for microstructure sensitivity in diffusion-weighted MR. Journal of Magnetic Resonance, 212(2), 344-354.
  8. Truffet, R., Rafael-Patino, J., Girard, G., Pizzolato, M., Barillot, C., Thiran, J. P., & Caruyer, E. (2020, October). An evolutionary framework for microstructure-sensitive generalized diffusion gradient waveforms. In International Conference on Medical Image Computing and Computer-Assisted Intervention (pp. 94-103). Springer, Cham.
  9. Moutal, N., Maximov, I. I., & Grebenkov, D. S. (2019). Probing surface-to-volume ratio of an anisotropic medium by diffusion NMR with general gradient encoding. IEEE Transactions on Medical Imaging, 38(11), 2507-2522.
  10. Rensonnet, G., Scherrer, B., Girard, G., Jankovski, A., Warfield, S. K., Macq, B., ... & Taquet, M. (2019). Towards microstructure fingerprinting: estimation of tissue properties from a dictionary of Monte Carlo diffusion MRI simulations. NeuroImage, 184, 964-980.
  11. Palombo, M., Alexander, D. C., & Zhang, H. (2019). A generative model of realistic brain cells with application to numerical simulation of the diffusion-weighted MR signal. Neuroimage, 188, 391-402.
  12. Topgaard, D. (2013). Isotropic diffusion weighting in PGSE NMR: numerical optimization of the q-MAS PGSE sequence. Microporous and mesoporous materials, 178, 60-63.
  13. Westin, C. F., Knutsson, H., Pasternak, O., Szczepankiewicz, F., Özarslan, E., van Westen, D., ... & Nilsson, M. (2016). Q-space trajectory imaging for multidimensional diffusion MRI of the human brain. Neuroimage, 135, 345-362.
  14. Cuntz, H., Forstner, F., Borst, A., & Häusser, M. (2010). One rule to grow them all: a general theory of neuronal branching and its practical application. PLoS computational biology, 6(8), e1000877.
  15. Palombo, M., Alexander, D. C., & Zhang, H. (2019). A generative model of realistic brain cells with application to numerical simulation of the diffusion-weighted MR signal. Neuroimage, 188, 391-402.

Figures

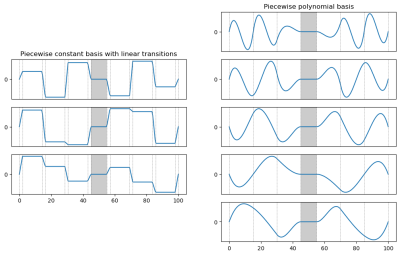
Figure 1. Example of two bases of gradient waveforms (arbitrary y-axis unit) for two gradient-encoding blocks of 45ms separated by 10ms dedicated to play the refocusing RF pulse (gray area). On the left, a solution is given for piecewise constant chunks separated with 2ms linear ramps; separation between chunks and ramps are indicated by dashed vertical lines. On the right, the solution corresponds to piecewise polynomial gradients of order 3 with $$$\mathcal{C}^1$$$ smooth transitions between the chunks.

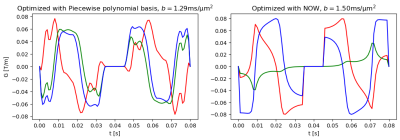
Figure 2. Gradient trajectories (x-, y- and z-gradients are represented in red, green and blue respectively) for spherical B-tensor encoding. The waveforms are optimized under constraints to maximize the trace of the B-tensor ($$$||g(t)||\leq 80$$$mT/m in each axis). The basis (left) is defined on 8 chunks with order 3, for a total of 15 degrees of freedom per axis. This is versatile enough to compare to the optimized solution obtained with NOW and 100 timesteps.

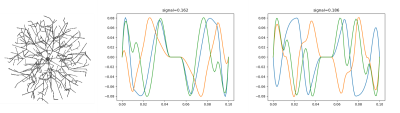
Figure 3. Example of a complex geometry, modeling a brain cell. The gradient trajectories reported next correspond to minimizing (left) or maximizing (right) the response signal, for the same target spherical B-tensor and b-value 3ms/µm$$$^2$$$.

Proc. Intl. Soc. Mag. Reson. Med. 31 (2023)
0978
DOI: https://doi.org/10.58530/2023/0978