Synopsis

Keywords: Microstructure, Diffusion/other diffusion imaging techniques

Estimating parameters of the Standard Model (SM) of white matter (WM) is an ill-posed problem (WM). To overcome this degeneracy, models extensions have been proposed adding echo-time dependent information. Here we investigate the feasibility of incorporating our analytical solution for the frequency shift from white matter axons accounting for magneto-structural anisotropy along with an empirical orientation dependence of relaxation into SM parameter estimation. This may also help achieving rotation-free mapping of susceptibility-related parameters using diffusion MRI instead of the impractical sample rotation in the scanner.

Introduction

Estimating parameters of the Standard Model (SM) of white matter (WM) is an ill-posed problem¹. Incorporating compartment-dependent isotropic transverse relaxation to SM² have been shown to have a potential for providing a deeper insight in the tissue microstructure. Recently, a 2-compartment model with isotropic diffusivity, frequency shift and relaxation has been proposed³. However, these extensions did not consider the anisotropy of the added quantities in WM e.g., orientation dependence w.r.t. the main field⁴. Here we investigate the feasibility of incorporating our analytical solution for the frequency shift from WM axons⁵ along with an empirical orientation dependence of relaxation^6,7 into SM parameter estimation. We hypothesize that this not only improves SM parameter estimation but also helps achieve rotation-free mapping of susceptibility-related parameters using diffusion MRI.

Methods

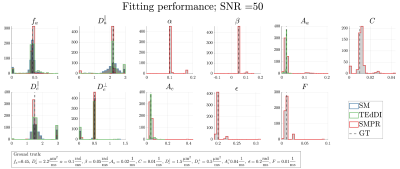
Theory: We propose to measure the normalized complex signal $$$S(b,\mathbf{\hat{g}},t)$$$, the SM with phase and relaxation (SMPR), from a multi-gradient-echo sequence, with diffusion weighting $$$(b,\mathbf{\hat{g}})$$$ and echo time $$$t$$$. The extra-axonal space exhibits a susceptibility-induced frequency shift of the form $$$\overline{\Omega}_e(\xi)=\alpha\xi^2+\epsilon$$$ and assumed relaxation $$${R^\ast}_{2e}(\xi)=A_e\xi^4+F$$$, while the intra-axonal compartment is $$$\overline{\Omega}_a(\xi)=\alpha\xi^2+\beta(1-\xi^2)+\epsilon$$$ and $$${R^\ast}_{2a}(\xi)=A_a\xi^4+C+F$$$, where $$$\xi=\mathbf{\hat{B}}\cdot\mathbf{\hat{n}}$$$ and $$$\mathbf{B}_0=\mathrm{B}_0\mathbf{\hat{B}}$$$ denotes the external field. While the functional form for the orientation dependence of compartmental relaxation was chosen in the spirit of the diffusion narrowing regime, the frequency shifts depend on WM susceptibility including anisotropy, as described by our analytical model⁵: $$$\alpha=-\gamma\mathrm{B}_01/2(\zeta\chi_\perp+1/6{\zeta\Delta\chi})$$$, $$$\beta=\gamma\mathrm{B}_0d/(2(d+d_w))\mathrm{ln}(g)\Delta\chi$$$ while $$$\epsilon$$$ includes all other frequency shifts (neighboring voxels, background sources etc.). Here $$$\gamma$$$ is the gyromagnetic ratio, $$$d$$$ and $$$d_w$$$ are the widths of myelin- and bilayers, respectively, g is the ratio between inner and outer radius of an axon, $$$\zeta$$$ the myelin volume fraction, while $$$\chi_\perp$$$ and $$$\Delta\chi$$$ is the perpendicular susceptibility and susceptibility anisotropy, respectively. The SMPR model can be seen in Figure 1.
Simulation: We investigate the feasibility of fitting SMPR from a simulated ground truth signal. The same is done for SM, TedDI (scalar relaxation for each compartment, here assumed to be the same size as $$$A_{a,e}$$$) for comparison in fitting performance. SNR was kept at 50. For SM and TEdDI we added Gaussian noise to avoid Rician bias correction, and the complex signal for SMPR has independent real and imaginary Gaussian noise. We use a highly dispersed Watson distribution for the fODF, $$$\mathcal{P}(\mathbf{\hat{n}})$$$, with scale parameter $$$\kappa=5$$$ ($$$p_2=0.65$$$ and $$$\theta_{p_2}=50$$$ degrees), and $$$\mathbf{\hat{B}}=\mathbf{\hat{z}}$$$, while the 11 parameters of the ground truth kernels are shown in Figure 1. We use $$$b=0,1,15$$$ ms/µm² with 75 directions in each shell generated using electrostatic repulsion, and $$$t=5,10,...,60$$$ ms. We fitted all models for 500 noise realizations and initial kernel parameter values randomly chosen in the intervals $$$0.1<f_a<0.9$$$, and $$$0.1<D<2.9$$$ µm²/ms for all diffusivities, while the frequency and relaxation parameters were within $$$\alpha,\beta\in[0.01;0.15]$$$ rad/ms, $$$A_{a,e},C\in[0.001;0.03]$$$ 1/ms, $$$F\in[0.005;0.02]$$$ 1/ms and $$$\gamma\in[0.1;0.3]$$$ rad/ms.

Results

Figure 2 shows histograms of estimated parameters for all three models. Here we found that SMPR produced the lowest variance in diffusivities and volume fraction, compared to SM and TEdDI, and successfully estimated the compartmental frequency shifts and relaxivities.

Discussion

The addition of $$$\overline{\Omega}_{a,e}(\xi)$$$ and $$$R^\ast_{2a,e}(\xi)$$$ to the Standard Model enabled estimation of compartmental susceptibility-induced frequency shifts and relaxivities without using sample rotations, at least when orientation dispersion is high. As the dispersion level decreases, so does the feasibility of fitting SMPR. However, by orienting the least orientationally dispersed WM (e.g. corpus callosum) at a 45 degree angle to the external field doubles the angular variation, and potentially improves fitting real data with less dispersion. This will be investigated in future studies. The SMPR model parameters for the frequency shifts define a set of rotationally invariant susceptibility parameters influenced by WM susceptibility anisotropy and geometry. We also found improved fitting stability of diffusivities and volume fraction when the initial frequency and relaxation values were not too far away from ground truth, but a more thorough investigation of the parameter landscape is needed and ongoing. Estimating the compartmental frequencies relies on the existence of non-negligible orientation dispersion, a valid assumption in WM tissue⁸, and the use of diffusion weighting to modulate the relative contributions from different fibers.
A recent study⁹ estimated the ratio between $$$\overline\chi_\perp$$$ and $$$\Delta\overline\chi$$$ to be around 5:1. As the largest frequency shift associated with $$$\Delta\overline\chi$$$ is through $$$\beta$$$ ⁵, then we may neglect anisotropy in $$$\alpha$$$ and $$$\epsilon$$$ as a first approximation, if sampling at multiple orientations is infeasible. Then, $$$\alpha$$$ provides an approximation of $$$\overline\chi_\perp$$$. Subtracting the contribution from $$$\overline\chi_\perp$$$ in $$$\epsilon$$$, we are left with a new parameter $$$\epsilon^\prime$$$ which depends on background fields and spherical sources. Thus, by running a QSM pipeline¹⁰ on $$$\epsilon^\prime$$$, we could potentially extract susceptibility $$$\overline\chi^S$$$ from spherical inclusions.
The orientation dependence of relaxation improves the estimation of underlying susceptibility parameters. While its functional form was empirically motivated here, analytical models are currently being developed: this will reduce the total number of degrees of freedom, as the mesoscopic frequency shifts and relaxation from internal fields share underlying parameters.

Conclusion

Adding orientation-dependent susceptibility effects to the Standard Model of diffusion in white matter enabled the estimation of compartmental frequency shifts and relaxation, which can be used to gain information about susceptibility properties of WM without impractical sample rotations.

Acknowledgements

This study is funded by the Independent Research Fund Denmark (grant 8020-00158B).