0974

Diffusion simulations in human myelinated axons from 3d EM evaluate the impact of realistic axon geometry on diameter mapping

Hong-Hsi Lee^1,2, Qiyuan Tian^1,2, Ricardo Coronado-Leija³, Els Fieremans³, Dmitry S Novikov³, and Susie Y Huang^1,2
¹Radiology, Athinoula A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Charlestown, MA, United States, ²Radiology, Harvard Medical School, Boston, MA, United States, ³Center for Advanced Imaging Innovation and Research, New York University School of Medicine, New York, NY, United States

Synopsis

Keywords: Validation, Microstructure

To disentangle the effect of complex features on axon diameter mapping, we segmented myelinated axons in a human brain electron microscopy data and use these to create artificial cylinders with undulations and caliber variations that can be tuned to varying degrees. Diffusion simulations in segmented real axons and artificial axons showed that undulations and beadings lead to overestimation and underestimation of the axon diameter, respectively.

Introduction

Diffusion MRI (dMRI) probes tissue microstructure at the mesoscopic scale and enables estimation of axonal and cellular dimensions. For example, at strong diffusion weighting $$$b$$$, the $$$1/\sqrt{b}$$$-scaling in directionally averaged (spherical mean) signals yields an estimate of axon diameter in the brain white matter (WM) [1,2]. Axon diameter mapping (ADM) using dMRI has been tested in perfectly straight cylinders and relatively straight, thick axons through explorations of the resolution limit [3-5]. The impact of realistic geometries (undulation, caliber variation) on diameter mapping has been demonstrated in mouse brain axons extracted from 3d electron microscopy (EM) [6], where axon size estimation is only accurate for straight axons at shorter time scales. However, the effect of undulation and caliber variation on ADM has not been fully explored in the human brain. Here, we segmented myelinated axons in a human brain EM sample and generated undulating, beaded cylinders with tuned undulations and caliber variations similar to those in real axons. Monte Carlo (MC) simulations of diffusion in segmented axons and artificial fibers showed that undulations and beading resulted in overestimation and underestimation of the axon diameter, respectively.

Method

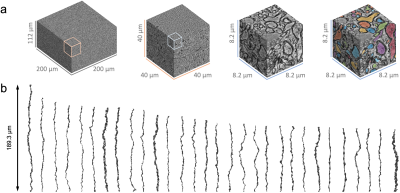
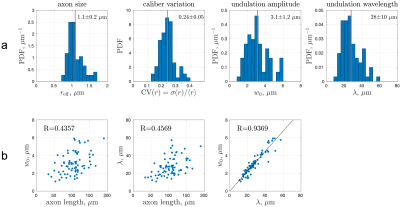
Human brain EM segmentation
Non-lesional brain tissue was obtained from the left middle temporal gyrus of a 47-year-old female during surgery for resection of an epileptogenic focus in the left hippocampus [7]. The tissue sample was trimmed to 2 x 3 x 0.2 mm³ and scanned with serial-section scanning EM. The 200 x 200 x 112 µm³ subset of subcortical WM was segmented using 2d/3d U-Net [8] (Fig. 1a), which was initially trained on ground truth segmentation of myelin and intra-axonal space (IAS) in EM of the mouse corpus callosum [9]. Voxel size was downsampled to (64 nm)³ after segmentation. Segmented IASs of myelinated axons longer than 33.5 µm were aligned along the z-axis, resulting in 76 axons ranging from 33.5-189.3 µm long (Fig. 1b). The effective MR radius $$$r_\text{eff}^4=\langle r^6\rangle/\langle r^2\rangle$$$ was calculated based on the equivalent circle radius $$$r$$$ [9] (Fig. 2a), and the undulation amplitude $$$w_0$$$ and wavelength $$$\lambda$$$ were calculated using a simplified 1-harmonic model for axonal skeletons [10] (Fig. 2a-b).

Undulating, beaded cylinders
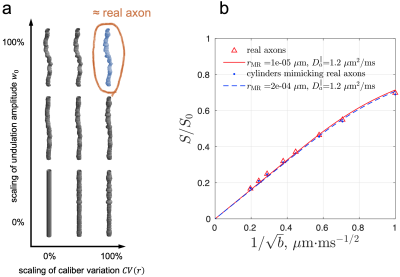
To mimic axonal geometry based on its most relevant features, we created (1) cylinders with the same undulations and caliber variations as in actual axons, and (2) cylinders with undulation amplitude $$$w_0$$$ and coefficient of variation of radius $$$\text{CV}(r)=\sigma(r)/\langle r\rangle$$$ each scaled from 0% to 100% (Fig. 3a).

MC simulations were implemented in CUDA C++ for diffusion in the 3d micro-geometry of IAS from 76 axons and their cylindrical derivatives. 100,000 random walkers/fiber were employed, diffusing 1.1 x 10⁵ steps with a duration 2.8 x 10^-4 ms and a step length 58 nm [10]. The intrinsic diffusivity was set to $$$D_0$$$= 2 µm²/ms. Diffusion signal of a pulsed gradient sequence was calculated, with the pulse duration $$$\delta$$$= 10 ms, pulse interval $$$\Delta$$$= 20 ms, eight b-values= 1-26 ms/µm², and 60 directions/b-shell.

Axon diameter mapping
Approximating real axons as a collection of cylindrical segments, the spherical mean signal is given by
$$\frac{S}{S_0}\simeq\beta\cdot b^{-1/2}\cdot e^{-bD_a^\perp}\cdot\text{erf}\left[(bD_a^\parallel)^{1/2}\right]\,,$$
where $$$\beta=(\pi/4D_a^\parallel)^{1/2}$$$, and $$$D_a^\parallel$$$ and $$$D_a^\perp$$$ are the IAS diffusivities along and transverse to the axonal segments [1]. The model was fit to the spherical mean MC signal, and the estimated $$$D_a^\perp$$$ was translated into the MR-estimated axon radius in Neuman’s limit [1,11]:
$$r_\text{MR}=\left( \frac{48}{7}\cdot\delta(\Delta-\delta/3)D_0D_a^\perp\right)^{1/4}\,.$$

Results

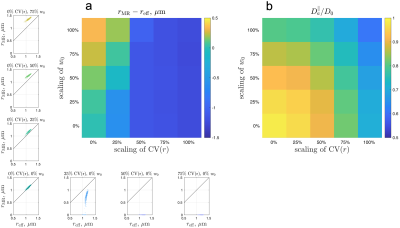
Simulated spherical mean dMRI signals in ex vivo human brain axons (Fig. 3b) yielded a radius estimate $$$r_\text{MR}$$$ < 0.001 µm, much smaller than the histological $$$r_\text{eff}\approx$$$1.1 µm. This bias may arise from axonal undulations and/or caliber variations. To determine the most relevant features contributing to this bias, we translated the real axons from ex vivo human EM into undulating, beaded cylinders with the same undulations and caliber variations, whose simulated signals were almost the same as those of real axons (Fig. 3b), and scaled these features to generate cylinders with varying caliber variation and undulation amplitude (Fig. 3a). The simulated spherical mean signals in the artificially generated cylinders led to radius estimates $$$r_\text{MR}$$$ greater than the histological $$$r_\text{eff}$$$ (overestimation) in the case of axons with strong undulations, and radius estimates smaller than the histological (underestimation) in the case of axons with strong caliber variations (Fig. 4a). The estimated axial diffusivity $$$D_a^\parallel$$$ decreased with undulations and caliber variations (Fig. 4b).

Discussion and Conclusions

ADM in WM is affected by strong undulations and/or caliber variations in axonal shape, as seen in fixed human brain tissue imaged by EM. Caliber variation is usually considered to be a major contributor to the overestimation of axon size [1,12,13]; however, our simulations show that caliber variations lead to underestimation of axon size in the actual model fitting. The $$$D_a^\parallel$$$ decrease with undulations and caliber variations is expected based on previous simulation studies [6,10,14,15]. The ex vivo sample was fixed by immersion in paraformaldehyde/glutaraldehyde solution [7], and undulations and caliber variations in fixed tissue may be stronger than in vivo. The relevance of these findings to ADM in vivo will requires further exploration and systematic multi-modality validation.

Acknowledgements

This study is support by NIH under the award number: DP5OD031854, R01NS118187, P41EB015896, P41EB030006, U01EB026996, S10RR023401, S10RR019307, S10RR023043, K99AG073506, R21NS081230, R01NS088040, P41EB017183.

References

1. Veraart, J., Nunes, D., Rudrapatna, U., Fieremans, E., Jones, D. K., Novikov, D. S., & Shemesh, N. (2020). Noninvasive quantification of axon radii using diffusion MRI. Elife, 9, e49855.

2. Fan, Q., Nummenmaa, A., Witzel, T., Ohringer, N., Tian, Q., Setsompop, K., ... & Huang, S. Y. (2020). Axon diameter index estimation independent of fiber orientation distribution using high-gradient diffusion MRI. Neuroimage, 222, 117197.

3. Nilsson, M., Lasič, S., Drobnjak, I., Topgaard, D., & Westin, C. F. (2017). Resolution limit of cylinder diameter estimation by diffusion MRI: The impact of gradient waveform and orientation dispersion. NMR in Biomedicine, 30(7), e3711.

4. Drobnjak, I., Zhang, H., Ianuş, A., Kaden, E., & Alexander, D. C. (2016). PGSE, OGSE, and sensitivity to axon diameter in diffusion MRI: Insight from a simulation study. Magnetic resonance in medicine, 75(2), 688-700.

5. Andersson, M., Kjer, H. M., Rafael-Patino, J., Pacureanu, A., Pakkenberg, B., Thiran, J. P., ... & Dyrby, T. B. (2020). Axon morphology is modulated by the local environment and impacts the noninvasive investigation of its structure–function relationship. Proceedings of the National Academy of Sciences, 117(52), 33649-33659.

6. Lee, H. H., Jespersen, S. N., Fieremans, E., & Novikov, D. S. (2020). The impact of realistic axonal shape on axon diameter estimation using diffusion MRI. Neuroimage, 223, 117228.

7. Shapson-Coe, A., Januszewski, M., Berger, D. R., Pope, A., Wu, Y., Blakely, T., ... & Lichtman, J. W. (2021). A connectomic study of a petascale fragment of human cerebral cortex. BioRxiv.

8. Tian, Q., Ngamsombat, C., Lee, H. H., Berger, D. R., Wu, Y., Fan, Q., ... & Huang, S. Y. (2020). Automated segmentation of human axon and myelin from electron microscopy data using deep learning for microstructural validation and simulation. In Proc. Int. Soc. Magn. Reson. Med. 4450.

9. Lee, H. H., Yaros, K., Veraart, J., Pathan, J. L., Liang, F. X., Kim, S. G., ... & Fieremans, E. (2019). Along-axon diameter variation and axonal orientation dispersion revealed with 3D electron microscopy: implications for quantifying brain white matter microstructure with histology and diffusion MRI. Brain Structure and Function, 224(4), 1469-1488.

10. Lee, H. H., Fieremans, E., & Novikov, D. S. (2021). Realistic Microstructure Simulator (RMS): Monte Carlo simulations of diffusion in three-dimensional cell segmentations of microscopy images. Journal of Neuroscience Methods, 350, 109018.

11. Neuman, C. H. (1974). Spin echo of spins diffusing in a bounded medium. The Journal of Chemical Physics, 60(11), 4508-4511.

12. Burcaw, L. M., Fieremans, E., & Novikov, D. S. (2015). Mesoscopic structure of neuronal tracts from time-dependent diffusion. NeuroImage, 114, 18-37.

13. Sepehrband, F., Alexander, D. C., Kurniawan, N. D., Reutens, D. C., & Yang, Z. (2016). Towards higher sensitivity and stability of axon diameter estimation with diffusion‐weighted MRI. NMR in Biomedicine, 29(3), 293-308.

14. Budde, M. D., & Frank, J. A. (2010). Neurite beading is sufficient to decrease the apparent diffusion coefficient after ischemic stroke. Proceedings of the National Academy of Sciences, 107(32), 14472-14477.

15. Lee, H. H., Papaioannou, A., Kim, S. L., Novikov, D. S., & Fieremans, E. (2020). A time-dependent diffusion MRI signature of axon caliber variations and beading. Communications biology, 3(1), 1-13.

Figures

Fig. 1. Non-lesional brain tissue was obtained from the left middle temporal gyrus and scanned with electron microscopy. (a) The (200 μm)³ subset of subcortical white matter was segmented using 2d/3d U-Net. (b) Segmented intra-axonal spaces of myelinated axons longer than 33.5 μm were aligned along the z-axis, resulting in 76 axons ranging from 33.5 to 189.3 μm long.

Fig. 2. Features of myelinated axons in the human white matter sample. (a) Effective MR radius and caliber variation were calculated based on the equivalent circle radius, and undulation amplitude and wavelength were calculated using a simplified 1-harmonic model for axonal skeletons. The mean (red line) and standard deviation are reported. (b) Undulation amplitude and wavelength are highly correlated, and both show much lower correlations with axon length.

Fig. 3. To mimic axonal geometry based on its most relevant features, we created (a) cylinders (blue) with the same undulations and caliber variations as real axons, and cylinders (gray) with undulation amplitude and coefficient of variation of radius scaled from 0% to 100%. (b) The simulated spherical mean signals in real axons (Fig. 1b) and axon-mimicking cylinders (Fig. 3a, blue) are consistent, and their MR-estimated axon radii < 0.001 μm are much shorter than the histological ground truth 1.1 μm in Fig. 2a.

Fig. 4. Axon size estimation based on diffusion simulations in undulating, beaded cylinders reveals the effect of undulations and caliber variations on axonal diameter mapping, respectively. (a) Simulations show that undulations lead to overestimation of axon size, and caliber variations lead to underestimation of axon size. (b) Both undulations and caliber variations lead to a decrease in intra-axonal axial diffusivity.

Proc. Intl. Soc. Mag. Reson. Med. 31 (2023)

0974

DOI: https://doi.org/10.58530/2023/0974