0971
Rotation-invariant microstructure mapping revisited
Daan Christiaens1,2, J-Donald Tournier3, Stefan Sunaert2,4, and Frederik Maes1,2
1Dept. of Electrical Engineering, ESAT/PSI, KU Leuven, Leuven, Belgium, 2Medical Imaging Research Center, UZ Leuven, Leuven, Belgium, 3Centre for the Developing Brain, School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom, 4Department of Imaging & Pathology, Translational MRI, KU Leuven, Leuven, Belgium
1Dept. of Electrical Engineering, ESAT/PSI, KU Leuven, Leuven, Belgium, 2Medical Imaging Research Center, UZ Leuven, Leuven, Belgium, 3Centre for the Developing Brain, School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom, 4Department of Imaging & Pathology, Translational MRI, KU Leuven, Leuven, Belgium
Synopsis
Keywords: Microstructure, Diffusion/other diffusion imaging techniques
Microstructure imaging with diffusion MRI relies on non-linear fitting of a biophysical tissue model to the data, often at low signal-to-noise ratio. In this work, we derive a new rotation-invariant feature set for microstructure mapping based on a rank-1 decomposition of the multi-shell diffusion MRI signal in spherical harmonics. Simulations show that using this feature set avoids non-central-χ bias that is present at low SNR in parameter estimation based on conventional rotation-invariants. Results in human brain imaging data acquired with free waveform diffusion encoding show robust parameter estimates across white matter.Introduction
Diffusion MRI (dMRI) is sensitive to tissue microstructure on a scale 2 – 3 orders of magnitude below the image resolution. Microstructure models of the dMRI signal response aim to identify more specific parameters of the tissue composition and how it is affected in pathology 1. However, robust microstructure imaging critically relies on accurate parameter estimators.In brain white matter, the dMRI signal is well represented as the spherical convolution of a single-fibre response function $$$H(\theta | B, \mathbf{x})$$$ and an orientation distribution function (ODF) $$$P(\mathbf{u})$$$ 2-4. The response function is often modelled as an intra-axonal “stick” compartment with fraction $$$f$$$ and axial diffusivity $$$D_i$$$ and an extra-cellular compartment with axial and radial diffusivities $$$D_e$$$ and $$$D_r$$$ 5,6. Microstructure mapping aims to estimate the vector of microstructure parameters $$$\mathbf{x}$$$ in each voxel for which this model best fits the acquired data.
Methods
Theory. In the basis of spherical harmonics (SH), spherical convolution of the microstructure kernel and ODF can be expressed as the outer product of a vector $$$\mathbf{h}_\ell = [ \ldots h_{\ell,B} \ldots]$$$ (indexed in $$$B$$$, the free-waveform diffusion encoding) and $$$\mathbf{p}_\ell = [ \ldots p_\ell^m \ldots]$$$ (indexed in $$$m$$$) in each harmonic band $$$\ell$$$ 4. Using this notation and assuming Gaussian noise, microstructure mapping solves a non-linear least-squares problem:$$ \min_{\mathbf{x}} \sum_\ell \| S_\ell - \mathbf{h}_\ell(\mathbf{x}) \mathbf{p}_\ell^\top \|^2 \quad, $$
where $$$S_\ell$$$ are matrices that structure the SH representation of dMRI signal per shell $$$B$$$ along the rows. Since, without noise, these matrices are of rank=1, we can approximate $$$\mathbf{p}_\ell = p_\ell \mathbf{v}_\ell$$$ where $$$\mathbf{v}_\ell$$$ is the leading right singular vector of $$$S_\ell \approx \mathbf{u}_\ell \sigma_\ell \mathbf{v}_\ell^\top$$$. Substituting into Eq. (1) leads to the equivalent cost function:
$$ \min_{\mathbf{x}} \sum_\ell \| \mathbf{r}_\ell - p_\ell \mathbf{h}_\ell(\mathbf{x}) \|^2 \quad, $$
where $$$\mathbf{r}_\ell = \sigma_\ell \mathbf{u}_\ell$$$ are voxel-level rank-1 SHARD features 4.
This equation corresponds to rotation-invariant microstructure fitting 6 except for the feature set that is used. Prior work used the SH power spectrum (also known as RISH-features), i.e., the norm of each row of $$$S_\ell$$$. These features are affected by non-central-χ bias at low SNR, whereas the derivation of Eq. (2) holds at any SNR.
Data. Data were collected in a healthy volunteer on a Philips 3T Achieva MRI using a 32-channel head coil. TE = 90ms; TR = 6000ms; slice thickness = 2.5mm; in-plane resolution = 2.5mm; MB = 2; SENSE = 2. The diffusion encoding comprises 3 shells with linear encoding at b=1000, 2000 and 5000 s/mm2, and 2 shells with bΔ = 0.6 at b=1000 and 2000 s/mm2, following 7. Each shell consists of 60 gradient directions, in addition to 16 b=0 images. Data were preprocessed with denoising 8, field unwarping 9, and motion correction 10.
Parameter fitting. We implemented rotation-invariant model fitting 6, using constrained Levenberg-Marquardt (LM) least-squares optimization with variable projection for the linear parameters $$$p_\ell$$$ 11. The Jacobian is calculated analytically. Iterative optimization is initialised using a Baysian Monte-Carlo estimator. All experiments are run at $$$\ell_{max} = 8$$$. The run time for full brain analysis is 1min 4sec on an Apple M1 Pro CPU.
Results
Simulations. Figure 1 plots the parameter landscape for a “true” value (black cross) set as the mean in white matter reported in 7 and using the chosen diffusion encoding scheme. We then simulated 100 realisations of Gaussian noise at SNR=30 and, initialised at the ground truth, and ran LM fitting using either RISH (orange) or SHARD (green) features. While the latter cluster around the ground truth, the RISH-based optimization shows significant bias in all parameters (univariate t-test to ground truth).Figure 2 repeats this experiment for a broad range of simulated ground truth values. While the RISH-based estimator introduces bias and even splits into two branches, the SHARD-based estimator is centred around a line of unit slope.
In vivo data. Figure 3 shows estimated parameter maps in human brain data. We find that usually $$$D_e > D_i$$$. Differences between RISH-based and SHARD-based estimators are less outspoken than the simulations predicted but arise in the extra-axonal diffusivity in the superior longitudinal fasciculus and the pallidum (Table 1).
Discussion and Conclusion
We presented a rederivation of rotation-invariant microstructure mapping with a subtle conceptual difference: instead of defining rotation-invariant features from the outset as a means to factor out the ODF, we showed that substituting the best model-free guess of the ODF results in a similarly compact feature set.The simulation results highlight a potential source of bias in RISH-based microstructure mapping. This non-central-χ bias is dominant at low SNR, i.e., at high b-values and at high SH order $$$\ell$$$. The simulations also illustrate that the feature set derived in Eq. (2) is not affected by this bias. Results in human brain data are more subtle, possibly due to non-Gaussian noise effects.
Despite clear improvements in parameter bias, the large variance of the fitted parameters (especially $$$D_e$$$ and $$$D_i$$$) in dMRI data at realistic SNR remains a considerable challenge for maximum-likelihood estimation. Future work can design Bayesian estimators 5 based on the proposed feature set.
Acknowledgements
DC is supported by the Flemish Research Foundation (FWO; grant number 12ZV420N).References
- Novikov DS, Kiselev VG, Jespersen SN. On modeling. Magn. Reson. Med. 2018; 79(6):3172-3193.
- Tournier J-D, Calamante F, Connelly A. Robust determination of the fibre orientation distribution in diffusion MRI: non-negativity constrained super-resolved spherical deconvolution. NeuroImage 2007; 5(4):1459-72.
- Jespersen SN, Kroenke CD, Ostergaard L, Ackerman JJ, Yablonskiy DA. Modeling dendrite density from magnetic resonance diffusion measurements. Neuroimage 2007; 34(4), 1473–1486.
- Christiaens D, Veraart J, Cordero-Grande L, Price AN, Hutter J, Hajnal JV, Tournier J-D. On the need for bundle-specific microstructure kernels in diffusion MRI. Neuroimage 2020; 208:116460.
- Reisert M, Kellner E, Dhital B, Hennig J, Kiselev VG. Disentangling micro from mesostructure by diffusion MRI: A Bayesian approach. Neuroimage 2017; 147:964-975.
- Novikov DS, Veraart J, Jelescu IO, Fieremans E. Rotationally-invariant mapping of scalar and orientational metrics of neuronal microstructure with diffusion MRI. Neuroimage 2018; 174:518-538.
- Lampinen B, Szczepankiewicz F, Mårtensson J, Westen D, Hansson O, Westin CF, Nilsson M. Towards unconstrained compartment modeling in white matter using diffusion-relaxation MRI with tensor-valued diffusion encoding. Magn Reson Med. 2020; 84:1605–1623.
- Veraart J, Novikov DS, Christiaens D, Ades-Aron B, Sijbers J, Fieremans E. Denoising of diffusion MRI using random matrix theory. NeuroImage 2016; 142:394-406.
- Andersson JLR, Skare S, and Ashburner J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. Neuroimage 2003; 20(2):870-888.
- Christiaens D, Cordero-Grande L, Pietsch M, Hutter J, Price AN, Hughes EJ, Vecchiato K, Deprez M, Edwards AD, Hajnal JV, Tournier J-D. Multi-shell SHARD reconstruction from scattered slice diffusion MRI data in the neonatal brain. NeuroImage 2021; 225:117437.
- O’Leary DP, Rust BW. Variable projection for nonlinear least squares problems. Computational Optimization and Applications 2013; 54(3):579-93.
Figures
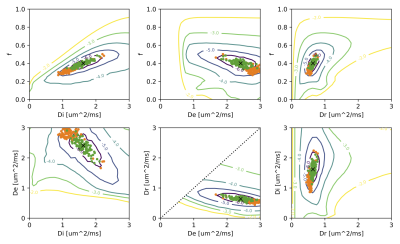
Figure 1: Optimization landscape of the model parameter space. Each plot shows the minimum value projection onto two parameter axes. The black cross marks the true value of the simulated model parameters. The orange and green dots depict the best fit to rotation-invariant RISH (orange) and SHARD (green) features for 100 noise instances simulated at SNR=30. These were obtained with Levenberg-Marquardt initialised at the ground truth. The RISH-based fit has significant bias to the true values.
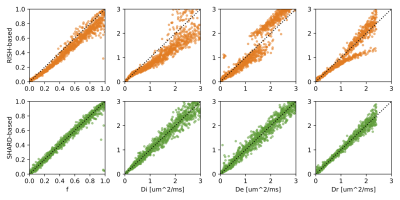
Figure 2: Accuracy of standard model parameter fitting based on RISH (top) and SHARD (bottom) features in simulated data with SNR=30. In each column, we varied one parameter while keeping all others fixed at the ground truth values shown in Fig. 1. The SHARD-based estimator is centred around a line of unit slope, whereas the RISH-based estimator shows clear bias and splits into two branches.
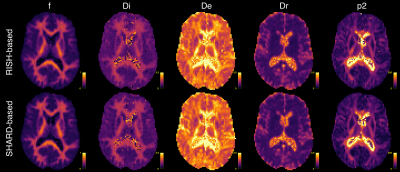
Figure 3: Estimated microstructure parameter maps in in vivo data using RISH-based (top) and SHARD-based (bottom) features and constrained Levenberg-Marquardt optimization.
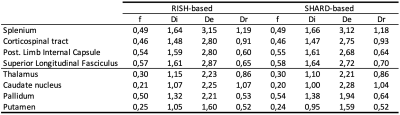
Table 1: Mean estimated parameter values in segmented white matter and subcortical grey matter structures.
DOI: https://doi.org/10.58530/2023/0971