Synopsis

Keywords: Spectroscopy, Machine Learning/Artificial Intelligence

We introduced a data-driven denoiser trained in a self-supervised fashion as a novel spatial-temporal constraint for MRSI reconstruction. Our proposed denoiser was trained using noisy data only via the Noise2void framework that trains an interpolation network exploiting the statistical differences between spatiotemporally correlated signals and uncorrelated noise. The trained denoiser was then integrated into an iterative MRSI reconstruction formalism as a Plug-and-Play prior. An additional physics-based subspace constraint was also included into the reconstruction. Simulation and in vivo results demonstrated impressive SNR-enhancing reconstruction ability of the proposed method, with improved performance over a state-of-the-art subspace method.

Introduction

A fundamental challenge in MR spatiospectral imaging is the limited SNR. Deep learning (DL) based image denoising methods have demonstrated superior performance on SNR enhancement than traditional analytical transforms and hand-crafted regularizations in different imaging applications^1-3. However, most DL-based denoisers are trained in a supervised fashion using large quantities of noisy and clean/high-SNR image pairs, which are extremely challenging to collect for MRSI. Motivated by the recent advancements in unsupervised/self-supervised learning strategies^2,4-6, we introduce here a new SNR-enhancing MRSI reconstruction method that incorporates a novel denoiser trained in a self-supervised fashion. Specifically, we adopted a Noise2Void⁵ strategy to learn an interpolation network from noisy data only to distinguish the spatiotemporally correlated spectroscopic signals of interest from the uncorrelated noise. We propose an ADMM Plug-and-Play⁷ (ADMM-PnP) algorithm to incorporate the trained network as a plug-in denoiser in an iterative reconstruction formalism. The subspace model with a physics-based, learned subspace was also integrated as an additional spatiotemporal constraint^8-9. The effectiveness of the proposed method was evaluated using simulation and in vivo data, demonstrating impressive SNR-enhancing and tissue-specific spectral feature preservation capabilities.

Theory and Methods

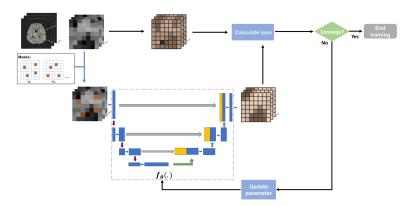
Self-supervised denoiser training
The recently proposed Noise2Void strategy trains a network to interpolate randomly masked pixels from their neighbors within image patches⁵. Assuming the noise is spatially independent, the trained interpolation network can then take noisy patches and output denoised results, without any noisy/clean image pairs. However, adapting this for MRSI data requires accounting for some unique signal characteristics. In particular, spatiotemporal correlations need to be exploited, and the spatial correlation of the signals is considered more local while the temporal FIDs have more global relations. Therefore, we propose a network to interpolate locally in space and globally in time. More specifically, we broke the high-dimensional data into spatially local patches each containing the entire FIDs, and randomly knocked out different voxels across different time points for training a network to interpolate the missing voxels. To this end, our UNet-based network, $$$f_\theta(.)$$$ , performs spatial convolution (local) and temporal fully-connected combinations (by treating the time dimension as the channel dimension) at the first layer. The subsequent layers follow a contracting and expanding path similar to UNet (Fig. 1). The training can be expressed as:
$$\widehat{\boldsymbol{\theta}}=\underset{\boldsymbol{\theta}}{\operatorname{min}} \sum_j\left\|f_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{\mathrm{P}(\{i\})}^j\right)-\boldsymbol{s}_{\{i\}}^j\right\|_2^2,\text{(1)}$$
where $$$\boldsymbol{x}_{\mathrm{P}(\{i\})}^j$$$ are training patches with index $$$j$$$ around a small collection of masked-out voxels indexed by $$$\{i\}$$$ with noisy values contained in vector $$$s_{\{i\}}^j$$$. This is self-supervised training, as both the input patches and the 'labels' $$$s_{\{i\}}^j$$$ come from the same noisy data. The data preparation and training strategies were illustrated in Fig. 1.

Reconstruction formulation and algorithm
With the pretrained denoiser $$$f_{\widehat{\theta}}(.)$$$, we formulate the reconstruction as:
$$\widehat{\mathbf{U}}=arg \underset{\mathbf{U}}{\operatorname{min}}\|A(\mathbf{U}\widehat{\mathbf{V}})-\mathbf{d}\|_2^2+\lambda_1 R(\mathbf{U}\widehat{\mathbf{V}})+\lambda_2\left\|\mathbf{D}_{\mathbf{w}} \mathbf{U}\widehat{\mathbf{V}}\right\|_2^2,\text(2)$$
where $$$A, \widehat{\mathbf{V}}, \mathbf{d}$$$ represents the spatiospectral encoding operator (with $$$B_0$$$ inhomogeneity modeling), learned temporal basis^9-10 and the noisy (k,t)-space data. The first regularization $$$R$$$ was enforced by the learned denoiser, and the second one is a spatial edge-preserving penalty term ( $$$\mathbf{D}_{\mathbf{w}}$$$ : edge-weighted finite different operator). Note that the third term is complementary and often used in denoising reconstruction but not required by the proposed method. To solve Eq. (2), we adopted the PnP-ADMM approach⁷ . More specifically, by introducing an auxiliary variable $$$\mathbf{H}$$$, the augmented Lagrangian form of (2) can be written as ( $$$\mathbf{Z}$$$ being the Lagrangian multiplier):
$$\widehat{\mathbf{U}},\widehat{\mathbf{H}},\widehat{\mathbf{Z}}=arg\underset{\mathbf{U},\mathbf{H},\mathbf{Z}}{\operatorname{min}}\left\|\mathcal{F}_{\mathbf{B}}(\mathbf{U} \widehat{\mathbf{V}})\mathbf{d}\right\|_2^2+\lambda_2\left\|\mathbf{D}_{\mathbf{w}} \mathbf{U}\widehat{\mathbf{V}}\right\|_2^2+\lambda_1 R(\mathbf{H})+\frac{u_1}{2}\left\|\mathbf{U}\widehat{\mathbf{V}}-\mathbf{H}+\frac{\mathbf{Z}}{u_1}\right\|_{\mathbf{F}}^2. \text(3)$$
For $$$k$$$-th iteration, we updated $$$\mathbf{H},\mathbf{U}$$$ and $$$\mathbf{Z}$$$ sequentially. With fixed $$$\mathbf{H}$$$, the update of $$$\mathbf{U}$$$ is essentially a $$$l_2$$$-regularized subspace fitting with a denoised prior. The update of $$$\mathbf{H}$$$ can be written as
$$\widehat{\mathbf{H}}^{k+1}=arg\underset{\mathbf{H}}{\operatorname{min}} \lambda_1R(\mathbf{H})+\frac{u_1}{2}\left\|\mathbf{U}^k \widehat{\mathbf{V}}\mathbf{H}+\frac{\mathbf{Z}^k}{u_1}\right\|_{\mathbf{F}}^2,\text{(4)}$$
which was replaced by applying the plug-in trained denoiser as a proximal operator:

$$\widehat{\mathbf{H}}=f_{\widehat{\boldsymbol{\theta}}}\left(\mathbf{U}^k \widehat{\mathbf{V}}+\frac{\mathbf{Z}^k}{u_1}\right).\text{(5)}$$

Other alternative PnP algorithms can be explored in this framework to incorporate the denoiser. For example, the RED¹¹ formalism absorbs the denoiser into a Laplacian-based regularization functional which has manageable gradient, and the MACE¹² approach provides a consensus equilibrium interpretation to the problem solved by PnP-ADMM which may provide further theoretical justification.

Results

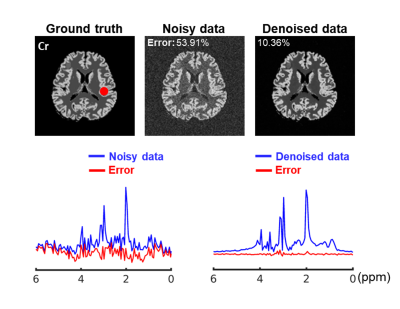
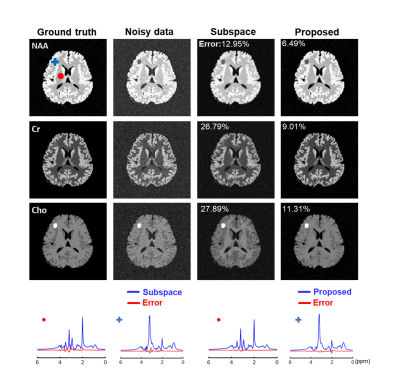
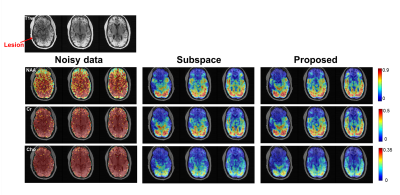
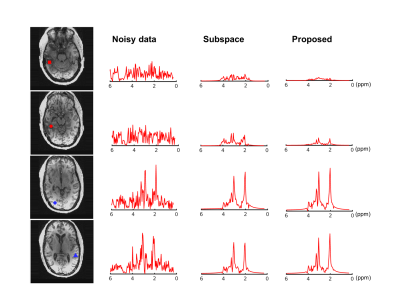
We first validated the proposed method using simulation. Specifically, 15 ¹H-MRSI datasets with different spectral parameters and spatial variations were created (matrix size=128×128 and 256 FID points)¹³. The network was trained with 2000 patches extracted from the simulated noisy data, with patch size=16×16×256 (FID points). Figure 2 illustrates the effectiveness of the trained denoiser (clear denoising effects observed). The denoiser was then plugged into the iterative reconstruction algorithm. Effective denoising reconstruction of metabolite maps and spectra were shown in Fig. 3. ¹H-MRSI data were acquired from Post-Traumatic Epilepsy patients on a Prisma 3T system using a 3D-EPSI sequence (IRB approved): TR/TE=1000/65 ms, FOV = 220×220×64 mm³, and matrix size=42×42×8. 2400 volumetric patches extracted from 4 subjects were used for denoiser training. A 3D UNet-like architecture was used to handle the 3D+t patches. Reconstructed metabolite maps and spectra from one patient were shown in Figs. 4-5, exhibiting impressive denoising effects while revealing clear contrast between normal tissues and lesion.

Conclusion

We presented a novel MRSI reconstruction method that synergizes a plug-in spatiotemporal denoising network trained in a self-supervised fashion and subspace modeling in an iterative formalism. Promising results from simulation and in vivo data were obtained.

Acknowledgements

This work was supported in part by NSF-CBET-1944249 and NIH-NIBIB-1R21EB029076A