0946
Physics-Informed Deep Learning Approach to Quantifying Magnetic Resonance Spectroscopy Data with Simultaneous Uncertainty Estimation1Institute of Scientific Instruments of the Czech Academy of Sciences Research institute in Brno, Brno, Czech Republic, 2Department of Biomedical Engineering, Brno University of Technology, Brno, Czech Republic, 3Magnetic Resonance Methodology, Institute of Diagnostic and Interventional Neuroradiology, University of Bern, Bern, Switzerland, Bern, Switzerland, 4Translational Imaging Center, sitem-insel, Bern, Switzerland
Synopsis
Keywords: Machine Learning/Artificial Intelligence, Spectroscopy, deep learning, machine learning, convolutional neural network, metabolite quantification, Bayesian neural network, variational autoencoder, epistemic uncertainty, aleatoric uncertainty
While deep learning (DL)-based approaches have been employed to quantify MRS signals, the interpretability of deep-model results and assessing what a DL model knows is a crucial component of DL-based approaches. We present a physics-informed DL-based algorithm for MRS data quantification with simultaneous uncertainty estimation, which uses the advantages of linear combination model fitting and the capabilities of ensembles of variational autoencoders. We acknowledge the need for further investigation with in-vivo datasets and other approaches. Furthermore, a more thorough analysis that includes scores that take estimation variation and uncertainty for both the proposed DL technique and traditional model fitting is required.
INTRODUCTION
In analyzing MRS signals, Cramér-Rao lower bounds are widely used to quantify the uncertainty of the model fit parameter estimation since direct access to the uncertainty is impossible without repeated measurements 1.Recently, deep learning (DL)-based approaches have been employed to quantify metabolites 2–6. However, it is often difficult to understand the interpretability of deep-model results. A key aspect is explaining or revealing how deep models make decisions.
It has been shown that an ensemble of neural networks trained with random initialization of parameters can quantify estimative uncertainty 7.
One prominent class of neural networks is variational autoencoders (VAEs), in which an encoder maps high-dimensional data to a low-dimensional embedding space parameterized by latent variables (the prior distribution, in Bayesian inference term), and a decoder reproduces the original data from the encoded space.
There are two types of uncertainty in Bayesian modeling 11 :(i) aleatoric uncertainty, which captures the uncertainty (noise) that exists inside the observations, and (ii) epistemic uncertainty, which accounts for uncertainty in the model parameters, whether the model does perfectly represent the data or not.
In this paper, we proposed a physics-informed DL method for MRS data quantification with aleatoric and epistemic uncertainties estimation, which uses the advantages of a linear combination model (LCM) and the capabilities of ensembles of VAEs.
METHODS
The simulated dataset, containing 96000 spectra, randomly shuffled into training (90%), validation (9%), and testing (1%) sets, was generated using a linear mixture of 19 amplitude-scaled metabolites from the publicly available basis set 8 with simulation parameters (amplitudes, common phase and frequency drifts, and common Lorentzian damping) chosen randomly from Gaussian distribution from in-vivo data 9, assuming tripled standard deviation. Macromolecule background (MMBG) components (13 Gaussian lineshapes, as reported in 10) were used to generate the lipid and MMBG basis signals.The mean frequency-domain Signal-to-Noise ratio (SNR) of the dataset was set to 295 ± 59 by introducing complex Gaussian white noise.
Moreover, an out-of-distribution dataset (128 spectra) was generated for testing purposes (the simulation parameters were chosen randomly from the Gaussian distributions assuming quintuple standard deviation, and the mean SNR was set to 118 ± 33).
A novel VAE architecture was proposed which incorporates parametric analysis (i.e., a model-based decoder 2,6) into a conventional VAE model (Fig. 1a). The proposed network is trained by minimizing the mean square error between input and outputs and the corresponding Kullback-Leibler divergence.
We utilized the deep ensembles approach 7 in which $$$M$$$ proposed VAEs with randomly initialized parameters were trained independently using the training dataset (Fig. 1b).
The final estimated metabolite content is equal to the average from the single estimation of each VAE 7.
Since each of the networks can estimate a mean and variance for each metabolite, the aleatoric uncertainty and epistemic uncertainty for each metabolite can be quantified as follows 7,11:
$$\bar{\mu}=\frac{1}{M}\sum_{i=1}^{M}\mu_i, (1)$$
$${\hat{\sigma}}^2=\ \frac{1}{M}\sum_{i=1}^{M}{\sigma_i}^2\ +\ \left[\left(\frac{1}{M}\sum_{i=1}^{M}\mu_i^2\right)\ -\ {\bar{\mu}\ }^2\right], (2)$$
where $$$\mu$$$ and $$$\sigma$$$ are the variational mean and standard deviation of the metabolite amplitude. The first term in Eq. 2 stands for aleatoric uncertainty, and the second term stands for epistemic uncertainty 11,12.
All training was performed using the mean-squared error loss (MSE) and an Adam optimizer 13 with a batch size of 128, a learning rate of 0.001, and 200 epochs. In this study, we set $$$M$$$ to 5.
The proposed VAEs were trained in a self-supervised fashion. Ground truth (GT) was exploited only for inference on estimations.
A traditional LCM fitting (i.e., QUEST 14,15) was used to compare the results. The MMBG signal was estimated with the QUEST subtract technique (the first 40 points were cut off, common phase and frequency drifts, and common Lorentzian damping for all metabolites).
RESULTS & DISCUSSION
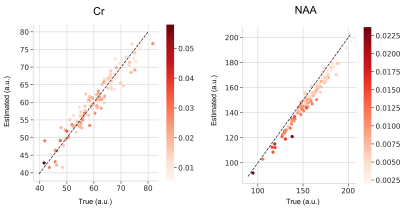
Figure 2 compares our proposed VAE vs. QUEST reporting symmetric mean absolute percentage error (SMAPE) with reference to the in-distribution test set. Figure 3a and 3b illustrate representative spectra from the in-distribution and out-of-distribution test spectra quantified by DL, along with the ground truth spectra, basis spectra, and estimated MMBG.Figure 4a and 4b show the quantified uncertainty of NAA and Cr estimations in in-distribution and out-of-distribution test sets as functions of SNR and accuracy of estimation. The negative correlation between SNR and aleatoric uncertainty in Figure 4 is consistent with the features of aleatoric uncertainty that relate to data intrinsic uncertainties, such as noise 11. Furthermore, aspects of epistemic uncertainty related to the model validity for the input test signal are consistent with the significantly higher epistemic uncertainty in out-of-distribution signals compared to in-distribution signals (Figure 4). This is in line with DL-based estimations that explore values at the edges of the latent space 16.
Figure 5 shows quantified aleatoric uncertainty in the estimated concentrations of Cr and NAA.
CONCLUSION
We demonstrated that a physics-informed DL architecture could be utilized for MRS data quantification with simultaneous uncertainty estimation by leveraging the advantages of LCM fitting and the capabilities of variational Bayesian. We are aware that more examination and comparison with in-vivo datasets and other methodologies are necessary. Moreover, a broader investigation with scores that include the variation and uncertainty of estimation of the proposed DL approach and traditional model fitting algorithms is needed.Acknowledgements
This project has received funding from the European Union's Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No 813120.References
1. Stagg C, Rothman D. Magnetic Resonance Spectroscopy: Tools for Neuroscience Research.; 2014.2. Gurbani SS, Sheriff S, Maudsley AA, Shim H, Cooper LAD. Incorporation of a spectral model in a convolutional neural network for accelerated spectral fitting. Magn Reson Med. 2019;81(5):3346-3357. doi:10.1002/mrm.27641
3. Lee HH, Kim H. Intact metabolite spectrum mining by deep learning in proton magnetic resonance spectroscopy of the brain. Magn Reson Med. 2019;82(1):33-48. doi:10.1002/mrm.27727
4. Hatami N, Sdika M, Ratiney H. Magnetic resonance spectroscopy quantification using deep learning. Lect Notes Comput Sci (including Subser Lect Notes Artif Intell Lect Notes Bioinformatics). 2018;11070 LNCS:467-475. doi:10.1007/978-3-030-00928-1_53
5. Chandler M, Jenkins C, Shermer SM, Langbein FC. MRSNet: Metabolite quantification from edited magnetic resonance spectra with convolutional neural networks. arXiv. 2019:1-12. doi:10.48550/arXiv.1909.03836
6. Shamaei AM, Starcukova J, Starcuk Z. Physics-informed Deep Learning Approach to Quantification of Human Brain Metabolites from Magnetic Resonance Spectroscopy Data. bioRxiv. October 2022:2022.10.13.512064. doi:10.1101/2022.10.13.512064
7. Lakshminarayanan B, Pritzel A, Blundell C. Simple and Scalable Predictive Uncertainty Estimation using Deep Ensembles. Adv Neural Inf Process Syst. 2016;2017-Decem:6403-6414. http://arxiv.org/abs/1612.01474. Accessed April 26, 2021.
8. Zöllner HJ, Považan M, Hui SCN, Tapper S, Edden RAE, Oeltzschner G. Comparison of different linear-combination modeling algorithms for short-TE proton spectra. NMR Biomed. 2021;34(4). doi:10.1002/nbm.4482
9. Mikkelsen M, Rimbault DL, Barker PB, et al. Big GABA II: Water-referenced edited MR spectroscopy at 25 research sites. Neuroimage. 2019;191:537-548. doi:10.1016/J.NEUROIMAGE.2019.02.059
10. Birch R, Peet AC, Dehghani H, Wilson M. Influence of macromolecule baseline on 1H MR spectroscopic imaging reproducibility. Magn Reson Med. 2017;77(1):34-43. doi:10.1002/mrm.26103
11. Kendall A, Gal Y. What uncertainties do we need in Bayesian deep learning for computer vision? Adv Neural Inf Process Syst. 2017;2017-Decem(Nips):5575-5585.
12. Gal Y. Uncertainty in Deep Learning. 2016.
13. Kingma DP, Ba JL. Adam: A method for stochastic optimization. In: 3rd International Conference on Learning Representations. International Conference on Learning Representations, ICLR; 2015. https://arxiv.org/abs/1412.6980v9. Accessed April 29, 2021.
14. Ratiney H, Sdika M, Coenradie Y, Cavassila S, van Ormondt D, Graveron-Demilly D. Time-domain semi-parametric estimation based on a metabolite basis set. NMR Biomed. 2005;18(1):1-13. doi:10.1002/nbm.895
15. Stefan D, Cesare F Di, Andrasescu A, et al. Quantitation of magnetic resonance spectroscopy signals: The jMRUI software package. Meas Sci Technol. 2009;20(10). doi:10.1088/0957-0233/20/10/104035
16. Rizzo R, Dziadosz M, Kyathanahally SP, Reyes M, Kreis R. Reliability of Quantification Estimates in MR Spectroscopy: CNNs vs Traditional Model Fitting. LNCS. 2022;13438:715-724. doi:10.1007/978-3-031-16452-1_68/FIGURES/7
Figures
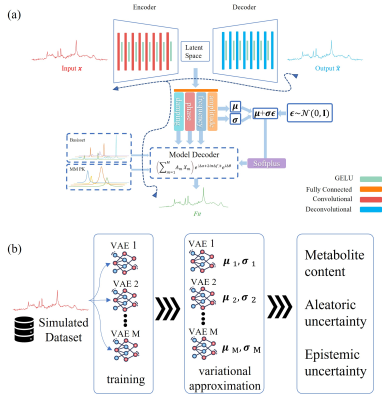
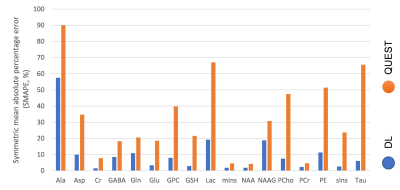
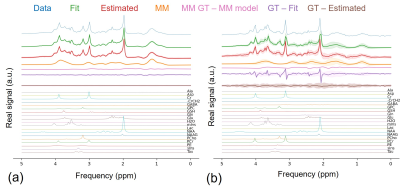
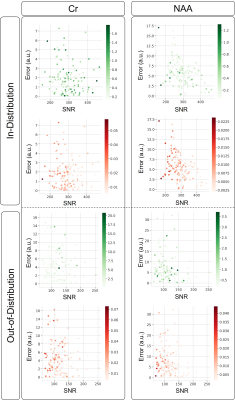
Figure 4. Testing results of the in-distribution and the out-of-distribution simulated dataset. Scatterplots illustrating concentration estimation error for NAA and Cr against SNR. Aleatoric and epistemic uncertainties are color-coded in shades of red and green, respectively. Systematic estimation errors are reported to a 2-fold factor higher (e.g., from ~[0-7] range to ~[0-16], for NAA), and epistemic uncertainty is found significantly higher (e.g., from ~[0.2-1.6] range to ~[2.5-20] for NAA)