Introduction

Diffusion tensor imaging (DTI) can noninvasively quantify the tissue microstructure by detecting the direction and extent of water molecules diffusion. DTI is widely used in disease diagnosis and nerve fiber tracking. However, diffusion-weighted (DW) images suffered from severe noise, especially for high-resolution imaging. The severe noise will reduce the accuracy of subsequent diffusion tensor estimation. In practice, it is usually to acquire much more than six DW images against the noise effect, which will further prolong scan time and increase costs. Therefore, it is highly desirable to estimate the accurate diffusion tensor from limited numbers of low signal-to-ratio (SNR) measurements.
Many post-processing approaches have been proposed to improve the accuracy of diffusion tensor estimation without increasing measurements. The traditional approaches are to denoise the image first to improve the SNR and then carry out parameter estimation. Among them, MPPCA ¹ and NLM ² denoising algorithms were commonly used. Recently, data-driven deep learning approaches ^3-5 are applied to estimate diffusion tensor, FA, and MD from a small number of measurements, which are superior in accuracy and speed to traditional methods. However, these deep learning methods are limited to the specific acquisition protocol of the training data.
Therefore, we proposed a novel model-based deep learning method for DTI tensor estimation. WLLS is adopted as data fidelity term to achieve an unbiased estimate, and RED ⁶ is used as regularization term using a CNN to remove noise. ADMM is adopted to decouple data fidelity terms and regularization terms for better optimization.

Methods

Simulated data:
The HCP diffusion MRI (dMRI) data from 24 healthy adults (16 for training, four for validation, and four for evaluation) were used in our study. The dMRI data (five b=0 and 64 b=1000) were denoised and corrected for Gibbs-ringing artifact and bias field using MRtrix software ⁷. After that, WLLS ⁸ was applied to yield high-quality diffusion tensor field (D) and non-DW images (S₀) from the pre-processed dMRI data. The calculated D and S₀ served as ground truth, and the DTI model was used to generate six DW images with six optimized diffusion-encoding directions⁹ :
$$S=S_{0}e^{-b\boldsymbol{g}^{T}\mathbf{D}\boldsymbol{g}}$$
where S is the reconstructed DW images with a given optimized encoding direction g, D is the diffusion tensor field, where each voxel can be represented by a 3×3 symmetric positive-definite matrix (with six unique elements). The Rician noise under different noise levels ranging from 0.005 to 0.045 was added to noise-free images.

Network structure:
To estimate diffusion tensor field D and non-DW images S₀, which can be represented as x=[S₀ D_xx D_yy D_zz D_xy D_yz D_xz], from log-transformed measurements y, we solve problem by minimizing the following objective function:
$$\hat{x}=\underset{x}{min}\sum_{i=1}^{N_{b}}\frac{W}{2\sigma^{2} }\left \|A_{i}x-y_{i} \right \|_{2}^{2}+\frac{\lambda }{2}x^{T}\left ( x-d\left ( x \right ) \right )$$
where $$$\sum_{i=1}^{N_{b}}\frac{W}{2\sigma^{2} }\left \|A_{i}x-y_{i} \right \|_{2}^{2}$$$ represents data consistency, W is a diagonal matrix with the diagonal elements proportional to DW images, σ² is the noise deviation, A is a mapping function from parameter maps to DW images with DTI model, $$$ x^{T}\left ( x-d\left ( x \right ) \right )$$$ is a regularization term, which adopts RED with a residual CNN denoiser $$$d\left ( \cdot \right )$$$, λ is regularization parameter. ADMM algorithm is used to optimize the objective function by constructing the augmented Lagrangian function:
$$\hat{x}=\sum_{i=1}^{N_{b}}\frac{W}{2\sigma^{2} }\left \|A_{i}x-y_{i} \right \|_{2}^{2}+\frac{\lambda }{2}z^{T}\left ( z-d\left ( z \right ) \right )+\left \langle \alpha,x-z \right \rangle+\frac{\rho }{2}\left \| x-z \right \|_{2}^{2} \; \; s.t. z=x$$
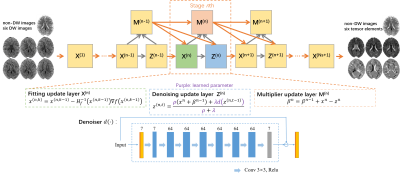
where α is Lagrangian multipliers, ρ is penalty parameter, z is auxiliary variable and the scaled Lagrangian multiplier $$$ \beta =\frac{\alpha }{\rho } $$$.The architecture of the deep unrolled network is shown in Fig.1. Gauss-Newton method, fixed point iteration method and gradient ascend method were applied to solve the following each subproblem, respectively:
$$\left\{\begin{matrix}x^{\left ( n,k \right )}=x^{\left ( n,k-1 \right )}-H_{f}^{-1}\left ( x^{\left ( n,k-1 \right )} \triangledown f(x^{\left ( n,k-1 \right )})\right )\\ z^{(n,t)}=\frac{\rho \left ( x^{n}+\beta ^{n-1} \; \right )+\lambda d\left ( z^{\left ( n,t-1 \right )\; \; } \right )}{\rho +\lambda }\\ \beta ^{n}=\beta ^{n-1}+x^{n}-z^{n}\end{matrix}\right.$$
where $$$n\in \left \{ 1,2,...,N_{s} \right \}, k\in \left \{ 1,2,...,N_{k} \right \}$$$ and $$$t\in \left \{ 1,2,...N_{t} \right \}$$$ index the stages, the iterations in fitting layer and denoising layer respectively.

Results

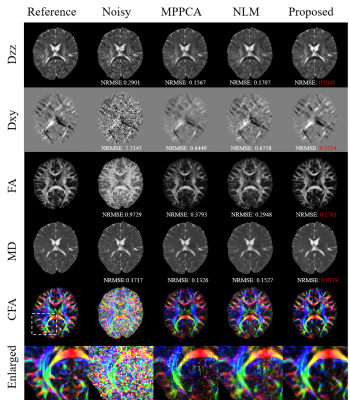
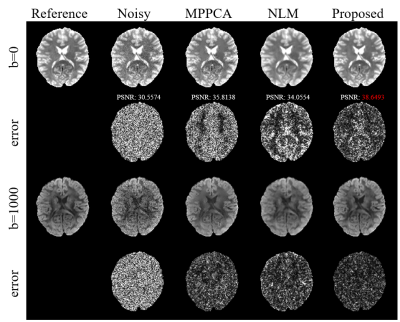
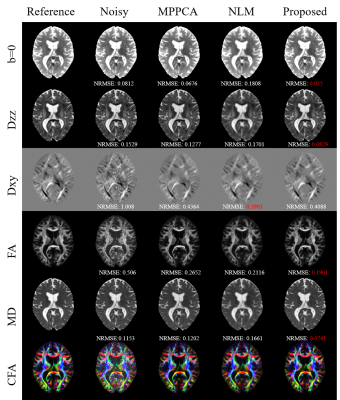
Fig.2 shows diffusion tensor maps and their corresponding tensor-derived parameters estimated from six-direction test data using different approaches. Both the tensor maps and DTI-derived parameter maps keep more detailed anatomical information with the smallest NRMSEs.
Fig.3 shows the non-DW images (b=0) and DW images (b=1000) and their corresponding error images for different methods on six-direction test data. It can be clearly seen that the reconstructed images by our method are closest to the reference with the smallest error.
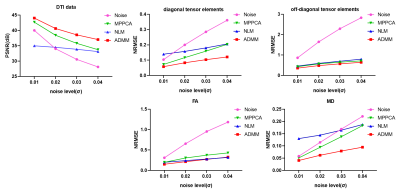
Fig.4 shows the qualitative results of DW images, diffusion tensor field, FA and MD maps of four test subjects. The proposed method yielded the highest PSNR and the lowest NRMSE than the compared methods across different noise levels.
Fig.5 shows parameter maps estimated with different approaches on 32-direction test data. The proposed method performed well on the test data acquired with different protocols.

Discussion and Conclusion

Preliminary experiments show that our proposed method can improve the accuracy of tensor estimation from the data acquired with different acquisition protocols. Model-driven deep learning method has strong generalization capacity and shows great practical application value.

Acknowledgements

This study was supported by the National Natural Science Foundation of China under Grant 61971214.