0941
Diffusion generative prior-based highly accelerated MR T1ρ mapping
Kangping Wang1, Chentao Cao1, Zhuoxu Cui1, Yuanyuan Liu1, Hairong Zheng1, Dong Liang1, and Yanjie Zhu1
1Shenzhen Institutes of Advanced Technology,Chinese Academy of Sciences, Shenzhen, China
1Shenzhen Institutes of Advanced Technology,Chinese Academy of Sciences, Shenzhen, China
Synopsis
Keywords: Machine Learning/Artificial Intelligence, Image Reconstruction
Diffusion-based generative models have been applied to solve the inverse problem of MR reconstruction and show impressive results. However, the diffusion model requires many iterations to produce high-quality samples, prolonging the reconstruction time. It also may lead to stochastic differential equation (SDE) sequence divergence in MR reconstruction and degrades the reconstruction quality. We proposed a new SDE for diffusion-based MR reconstruction that focuses on the diffusion process in high-frequency of k-space to improve reconstruction robustness and reduce the iterations. We applied the proposed method in MR T1ρ mapping, showing that it can achieve a high acceleration of 14X.Introduction
MR T1ρ mapping is an important tool for characterizing intrinsic tissue information. However, the long acquisition time greatly hinders its wide clinical use. Deep learning (DL)-based reconstruction methods have been used as a powerful tool to accelerate MR imaging [1]. One main strategy of DL-based methods is using the end-to-end supervised technique to learn the mapping from undersampled k-space data to images. But this strategy is trained for specific imaging anatomy and shows degraded reconstruction quality when applied out of distribution. Another strategy is based on distribution-learning approaches, which use the pre-trained generative models as priors to solve the inverse problems of MR image reconstruction. Recently, the diffusion-based generative model has shown great performance in many scenarios[2,3]. It has been applied in MR reconstruction and shows impressive results. However, diffusion models often require multiple iterations to produce high-quality samples, extending reconstruction time. From an optimization point of view, the inverse time VP-SDE can be seen as a stochastic gradient Langvien descent algorithm. According to the analysis of solving practical problems, the reverse process of VP-SDE can be regarded as maximizing the energy of reconstructing MR images, which tends to cause SDE sequence divergence and reduce the reconstruction quality. In this study, we proposed a new SDE for diffusion-based MR reconstruction that focuses on the diffusion process in high-frequency of k-space, namely high-frequency SDE diffusion model (HFS-SDE) to improve reconstruction robustness and reduce the iterations. We applied the proposed method in MR T1ρ mapping, showing that it can achieve a high acceleration of 14X.Method
Since the image energy is mainly concentrated in the low-frequency region, we construct a diffusion process in the high-frequency region of the k-space. The low- and high-frequency operators are defined as $$\begin{gathered}\mathcal{F}_l\left(\mathbf{x}_i\right):=\sum_{j=1}^n \mathbf{c s m}_j^* \cdot \mathbf{F}^{-1}\left(\mathbf{M}_l \cdot F\left(\operatorname{csm}_j \cdot \mathbf{x}_i\right)\right) \\\mathcal{F}_h\left(\mathbf{x}_i\right):=\sum_{j=1}^n \mathbf{c s m}_j^* \cdot \mathbf{F}^{-1}\left(\left(\mathbf{I}-\mathbf{M}_l\right) \cdot F\left(\mathbf{c s m}_j \cdot \mathbf{x}_i\right)\right)\end{gathered},$$where $$$\mathcal{F}_h$$$represents the high-frequency operator, $$$\mathcal{F}_l$$$ represents the low-frequency operator, $$$\mathbf{c s m}_j^*$$$ represents the $$$\mathcal{j}$$$th coil sensitivity of $$$\mathcal{j}$$$-receiver coil. $$$\mathbf{F}$$$ is the Fourier operator, $$$\mathbf{M}_l$$$ is the mask that extracts k-space center, and $$$\mathbf{I}$$$ represents the unit matrix.The forward diffusion process of HSF-SDE can be rewritten as:$$\mathbf{x}_i=\mathcal{F}_l\left(\mathbf{x}_{i-1}\right)+\sqrt{1-\beta_i} \mathcal{F}_h\left(\mathbf{x}_{i-1}\right)+\sqrt{\beta_i} \mathcal{F}_h\left(\mathbf{z}_{i-1}\right), i=1, \cdots, N,$$ where $$$\left\{\beta_1, \beta_2, \ldots, \beta_N\right\}$$$ is the given coefficient to control the noise level and $$$\mathbf{z}_{i-1} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$$$ , the diffusion process adds Gaussian noise to the input data through N times of accumulation, and the normal distribution $$$\mathbf{z}_{i-1} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$$$. When $$$N \rightarrow \infty,\left\{N \beta_i\right\}_{i=1}^N$$$ a can be written as $$$\beta_1$$$ and $$$t \in[0,1]$$$ . The forward diffusion process of HSF-SDE can converge to $$\mathrm{d} \mathbf{x}=-\frac{1}{2} \beta(t) \mathcal{F}_h(\mathbf{x}) \mathrm{d} t+\sqrt{\beta(t)} \mathcal{F}_h \mathrm{~d} \mathbf{w}.$$
Proposed by Särkkä and Solin [4] and let $$$\beta(t)=\bar{\beta}_{\min }+t\left(\bar{\beta}_{\max }-\bar{\beta}_{\min }\right), t \in[0,1]$$$. The HFS-SDE discrete form of the perturbation core can be exported as:$$\begin{aligned}&p_{0 t}(\mathbf{x}(t) \mid \mathbf{x}(0)) \\&=\mathcal{N}\left(\mathbf{x}(t) ; e^{\left(-\frac{1}{4} t^2\left(\bar{\beta}_{\max }-\bar{\beta}_{\min }\right)-\frac{1}{2} t \bar{\beta}_{\min }\right) \mathcal{F}_h} \mathbf{x}(0), \mathbf{I}-\mathbf{I} e^{\left(-\frac{1}{2} t^2\left(\bar{\beta}_{\max }-\bar{\beta}_{\min }\right)-t \bar{\beta}_{\min }\right) \mathcal{F}_h}\right), t \in[0,1]\end{aligned}. $$Our goal is to reconstruct MR images based on the acquired k-space data y. Based on the trained network, we can perform the following inverse HFS-SDE condition on y to obtain the reconstructed image[5]:$$\mathrm{d} \mathbf{x}=\left(-\frac{1}{2} \beta(t) \mathcal{F}_h(\mathbf{x})-\beta(t) \mathcal{F}_h\left(\nabla_{\mathbf{x}} \log p_t(\mathbf{x} \mid \mathbf{y})\right)\right) \mathrm{d} t+\sqrt{\beta(t)} \mathcal{F}_h \mathrm{~d} \overline{\mathbf{w}}. $$The specific reconstruction process is shown in Figure 1.
Datasets: The brain dataset was collected from 12 volunteers using a 3D T1ρ mapping sequence at 5T MR [6]. 5T scanner (Jupiter, United Imaging Healthcare, Shanghai, China). The sequence was implemented by an adiabatically prepared constant-amplitude spin-lock preparation pulse followed by a segmented gradient echo (GRE) readout. Imaging parameters were: FOV = 240×200×90 mm2, Voxel size = 1×1×3 mm3, TR/TE = 7.48/3.70 ms, times of spin lock (TSLs) = 0, 25, 45, and 65 ms. The 3D image volume is divided into 2D slices and several layers are taken out for training and testing. There were a total of 798 images, which were divided into training data 748 and testing data 50.
RESULTS and DISCUSSION
Figure 2 shows the reconstructed T1ρ-weighted images and the corresponding maps of the coronal view using HFS-SDE at acceleration factors of 10, 12, and 14. The reconstruction results of VP-SDE are also shown for comparison. We calculated the normalized root mean squared error (nRMSE) of each image. The nRMSE is shown in the lower right corner of each image. As can be seen from the results, the reconstructed images using HFS-SDE show little artifacts and have lower nRMSE compared with those using VP-SDE. Figure 3 shows the reconstructed results in the sagittal view. A similar conclusion can be drawn from Figure 3 as from figure 2.CONCLUSION
The proposed HFS-SDE method[7] improves the stability of the diffusion model and achieves a high acceleration in T1ρ mapping at 5T.Acknowledgements
Kangping Wang and Chentao Cao contributed equally to this work. This study is supported by the National Key R&D Program of China no. 2020YFA0712200, National Natural Science Foundation of China under grant no. 81971611,62125111, 81901736, 62201561 and U1805261;Shenzhen Science and Technology Program under grant no.RCYX20210609104444089.References
- Dai, X., Lei, Y., Fu, Y., Curran, W.J., Liu, T., Mao, H., Yang, X.: Multimodal mrisynthesis using unified generative adversarial networks. Medical physics 47(12),6343–6354 (2020)
- Ho, J., Jain, A., & Abbeel, P. (2020). Denoising diffusion probabilistic models. Advances in Neural Information Processing Systems, 33, 6840-6851.
- Song, Y., Shen, L., Xing, L., & Ermon, S. (2021). Solving inverse problems in medical imaging with score-based generative models. arXiv preprint arXiv:2111.08005.
- Särkkä, S., & Solin, A. (2019). Applied stochastic differential equations (Vol. 10). Cambridge University Press.
- Anderson, B. D. (1982). Reverse-time diffusion equation models. Stochastic Processes and their Applications, 12(3), 313-326.
- Liu, Y., Wang, W., Zheng, Y., Wang, H., Zheng, H., Liang, D., & Zhu, Y. (2022). Magnetic resonance T1ρ quantification of human brain at 5.0 T: A pilot study. Frontiers in Physics, 1004.
- Cao, C., Cui, Z. X., Liu, S., Liang, D., & Zhu, Y. (2022). High-Frequency Space Diffusion Models for Accelerated MRI. arXiv preprint arXiv:2208.05481.
Figures
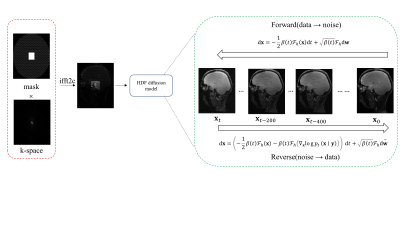
Figure
1: The
forward noise addition process and the reverse denoising process
(reconstruction) for the high-frequency region in the network.
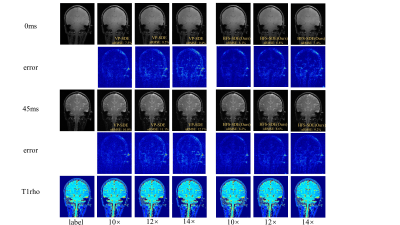
Figure 2: Reconstructed T1ρ-weighted images and the corresponding maps of the coronal view using VP-SDE and HFS-SDE at acceleration factors of 10, 12, and 14.
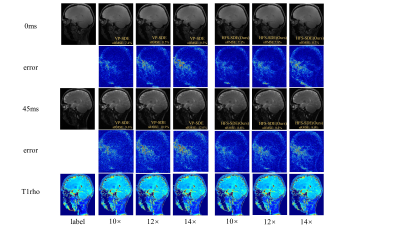
Figure 3: Reconstructed T1ρ-weighted images and the corresponding maps of the coronal view using VP-SDE and HFS-SDE at acceleration factors of 10, 12, and 14.
DOI: https://doi.org/10.58530/2023/0941