0940
Joint Reconstruction of Image Repetitions in DWI using Cross-Instance Attention1Pattern Recognition Lab, Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen, Germany, 2MR Application Predevelopment, Siemens Healthcare GmbH, Erlangen, Germany
Synopsis
Keywords: Machine Learning/Artificial Intelligence, Image Reconstruction, Transformer, Multiple Instance Learning
Despite its proven clinical value, Diffusion-weighted Imaging (DWI) suffers from several technical limitations associated with prolonged echo trains in single-shot sequences. Parallel Imaging with sufficiently high under-sampling enabled by Deep Learning-based reconstruction may mitigate these problems. Newly emerged architectures relying on transformers demonstrated high performance in this context. This work aims at developing a transformer-based reconstruction method tailored to DWI by utilizing the availability of multiple image instances for a given slice. Redundancies are exploited by jointly reconstructing images using attention mechanisms which are performed across the set of instances. Benefits over reconstructing images separately from each other are demonstrated.Introduction
Diffusion-weighted imaging (DWI) based on single-shot echo-planar imaging (ssEPI) is valuable as a cancer biomarker in many clinical applications1-3. To mitigate adverse effects of long echo trains (low SNR, limited resolution, geometrical distortions), DW-ssEPI is oftentimes acquired using parallel imaging (PI) with regular Cartesian under-sampling in k-space. While conventional reconstruction methods4,5 for PI tend to introduce artifacts at acceleration factors $$$R>2$$$, methods based on Deep Learning have shown to allow higher accelerations in non-DWI applications6. As an alternative to commonly used convolutional neural networks (CNNs), vision transformers7,8 based on (self-)attention mechanisms9 have been proposed with recent works reporting superior results compared to CNNs in the context of MR reconstruction10,11. Given this success as well as the fact that slices are acquired repetitively in DWI for SNR purposes, the goal of this work was to develop a transformer-based reconstruction method for DWI in which the attention operations effectively exploit redundancies in the set of image instances.Methods
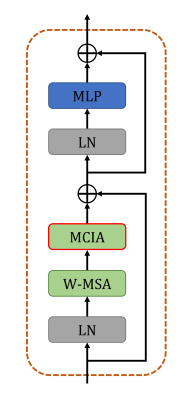
Architecture: The proposed method uses an unrolled network scheme which alternates between a learned regularizer and data consistency blocks12. The architecture of the regularizer network is illustrated in Figure 1. It follows the shape of a U-Net13 with a down-sampling (encoder) and up-sampling (decoder) path as well as skip connections in between. Here, a pair of Swin-Transformer8 blocks (STB) followed by a Patch Merging8 module is used in every encoder stage, whereas a stage in the decoder path comprises two convolution layers preceded by a Pixel Shuffle module14. To enable joint reconstruction of image repetitions, an additional module referred to as Multi-head Cross-Instance Attention (MCIA) is inserted into the standard STB (see Figure 2). In contrast to the spatial self-attention within windows (W-MSA), MCIA computes attention across the dimension which contains the set of image instances following the idea of previous works in the context of multiple instance learning15,16.Data: Liver DWI with b-values of 50 and 800 s/mm2 (5 and 15 repetitions, respectively) was acquired in 37 healthy subjects on 1.5 and 3T MR scanners (MAGNETOM, Siemens Healthcare, Erlangen, Germany) using an ssEPI research application sequence. Data of the subjects were divided into training, validation, and test splits (31/3/3). Raw data was acquired with a prospective acceleration of $$$R=2$$$ with ground-truth images generated by a scanner-integrated reconstruction. Coil sensitivities were estimated on separate low-resolution reference scans.
Experiments: For training and evaluation purposes, data was retrospectively under-sampled to $$$R=4$$$ with network inputs obtained by a Tikhonov-regularized SENSE4 reconstruction. The proposed multiple instance reconstruction (MIR) was compared with single instance reconstruction (SIR) using the baseline network architecture without the addition of MCIA. Both networks were unrolled for 5 iterations and trained for 100 epochs with early stopping while minimizing a loss function of the form $$$L_1+0.5·L_{perc}$$$ where the first term is a pixel-wise L1-penalty and the second term represents a perceptual loss17. Tensors representing network inputs and outputs had two channels holding real and imaginary parts, respectively, while the set of image repetitions was represented in the batch dimension. In contrast to MIR in which the output repetitions were averaged prior to loss computation, the loss was computed on the single repetitions in the case of SIR. Reconstruction quality was evaluated qualitatively as well as quantitatively using peak signal-to-noise ratio (PSNR) and structural similarity (SSIM).
Results
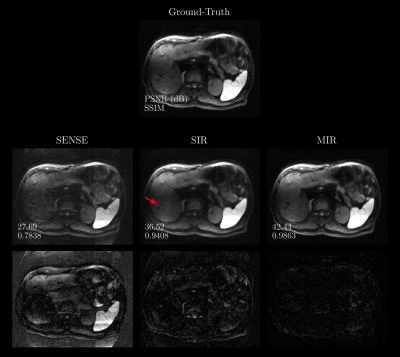
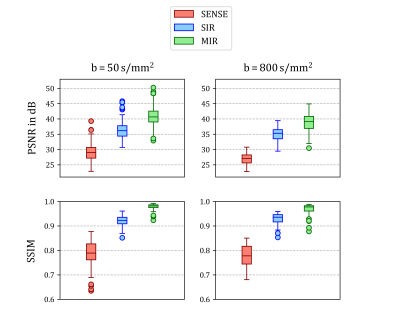
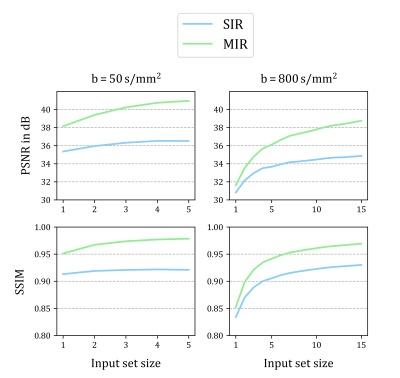
A qualitative comparison on a representative image from the test set is presented in Figure 3. At $$$R=4$$$, the SENSE reconstruction leads to excessive noise amplification and fails to remove aliasing sufficiently. In the SIR setting, the reconstruction appears blurry which is most apparent at fine structures such as vessels. In contrast, the regularizing effect of jointly reconstructing repetitions in MIR provides an image with higher visual fidelity to the ground-truth as well as improved image quality metrics. The quantitative evaluation on the entire test data set provided in Figure 4 underlines the benefits of joint reconstruction as MIR outperforms SIR across b-values by +4.05 dB and +0.048 in terms of PSNR and SSIM, respectively. Figure 5 demonstrates that reconstruction quality improves with growing input set size. Interestingly, MIR outperforms SIR in the case of a single image repetition as input, although the latter was trained for this specifically while the former was provided with varying set sizes (5-15) as input during training.Discussion & Conclusion
This work demonstrates that utilizing the availability of redundant image information in the form of repetitive acquisitions can greatly benefit reconstruction quality of DWI with high accelerations. Using a network architecture based on attention operations allows parameter-efficient incorporation of multiple instance learning. Compared to the baseline architecture, inclusion of the MCIA module led to an increase in parameters of approximately 5%. Further, the proposed implementation allows to ensure important properties for set-structured inputs, such as support of variable set sizes and permutation equivariance18.Acknowledgements
No acknowledgement found.References
1) Taouli, B., & Koh, D. M. (2010). Diffusion-weighted MR imaging of the liver. Radiology, 254(1), 47-66.
2) Maier, S. E., Sun, Y., & Mulkern, R. V. (2010). Diffusion imaging of brain tumors. NMR in biomedicine, 23(7), 849-864.
3) Le Bihan, D., & Iima, M. (2015). Diffusion magnetic resonance imaging: what water tells us about biological tissues. PLoS biology, 13(7), e1002203.
4) Pruessmann, K. P., Weiger, M., Scheidegger, M. B., & Boesiger, P. (1999). SENSE: sensitivity encoding for fast MRI. Magnetic Resonance in Medicine, 42(5), 952-962.
5) Griswold, M. A., Jakob, P. M., Heidemann, R. M., Nittka, M., Jellus, V., Wang, J., ... & Haase, A. (2002). Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magnetic Resonance in Medicine, 47(6), 1202-1210.
6) Muckley, M. J., Riemenschneider, B., Radmanesh, A., Kim, S., Jeong, G., Ko, J., ... & Knoll, F. (2021). Results of the 2020 fastmri challenge for machine learning MR image reconstruction. IEEE transactions on medical imaging, 40(9), 2306-2317.
7) Dosovitskiy, A., Beyer, L., Kolesnikov, A., Weissenborn, D., Zhai, X., Unterthiner, T., ... & Houlsby, N. (2020). An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. In International Conference on Learning Representations.
8) Liu, Z., Lin, Y., Cao, Y., Hu, H., Wei, Y., Zhang, Z., ... & Guo, B. (2021). Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision (pp. 10012-10022).
9) Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., ... & Polosukhin, I. (2017). Attention is all you need. Advances in neural information processing systems, 30.
10) Lin, K., & Heckel, R. (2021). Vision Transformers Enable Fast and Robust Accelerated MRI. In Medical Imaging with Deep Learning.
11) Huang, J., Fang, Y., Wu, Y., Wu, H., Gao, Z., Li, Y., ... & Yang, G. (2022). Swin transformer for fast MRI. Neurocomputing, 493, 281-304.
12) Aggarwal, H. K., Mani, M. P., & Jacob, M. (2018). MoDL: Model-based deep learning architecture for inverse problems. IEEE transactions on medical imaging, 38(2), 394-405.
13) Ronneberger, O., Fischer, P., & Brox, T. (2015). U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical image computing and computer-assisted intervention (pp. 234-241). Springer, Cham.
14) Shi, W., Caballero, J., Huszár, F., Totz, J., Aitken, A. P., Bishop, R., ... & Wang, Z. (2016). Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 1874-1883).
15) Ilse, M., Tomczak, J., & Welling, M. (2018, July). Attention-based deep multiple instance learning. In International conference on machine learning (pp. 2127-2136). PMLR.
16) Lee, J., Lee, Y., Kim, J., Kosiorek, A., Choi, S., & Teh, Y. W. (2019, May). Set transformer: A framework for attention-based permutation-invariant neural networks. In International conference on machine learning (pp. 3744-3753). PMLR.
17) Zhang, R., Isola, P., Efros, A. A., Shechtman, E., & Wang, O. (2018). The unreasonable effectiveness of deep features as a perceptual metric. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 586-595).
18) Zaheer, M., Kottur, S., Ravanbakhsh, S., Poczos, B., Salakhutdinov, R. R., & Smola, A. J. (2017). Deep sets. Advances in neural information processing systems, 30, 3391-3401.Figures
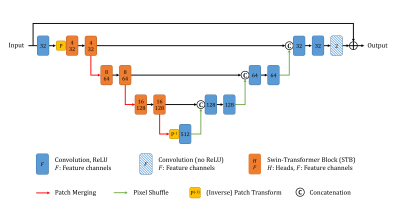
Figure 1: Overview of the regularizer architecture. It differs from a U-Net in that it employs Swin-transformer Blocks (STBs) for the encoding path instead of convolutions. Further, Patch Merging is used for down-sampling by a factor of 2 and doubling the number of feature channels. Following the first convolution layer of the network, feature maps are sub-divided into patches of size $$$4×4$$$ for compatibility with the STBs. After the last STB, the patch transform is reversed. In the decoder path, Pixel Shuffle modules are used for up-sampling the feature maps by factors of 2.