Synopsis

Keywords: CEST & MT, Quantitative Imaging

Most quantitative magnetization transfer imaging (qMT) protocols require additional T1 mapping scan. A recent on-resonance multiple phase-cycle bSSFP method was proposed for qMT that obviates the necessity for T1 mapping, but the fitting results were suboptimal. In this study, we proposed a physics-informed artificial neural network (ANN) to improve the fitting of this method. By using the MR signal model to generate the training data and regularize the network, no in-vivo data acquisition was necessary. Experiments on digital phantom and in-vivo data demonstrated improvement over previous method and better resilience against measurement noise.

Introduction

Several acquisition methods have been proposed for quantitative magnetization transfer (qMT) imaging, but most require separate T₁ mapping to constrain the signal model^1,2,11. Recently, an on-resonance multiple phase-cycle bSSFP model was proposed for qMT (mPC-bSSFP-qMT) that does not require separate T₁ mapping³ by using the elliptical profile of bSSFP signal⁴. The method can produce good T₁ and T₂ values, but the fitting of qMT parameters was suboptimal. In this study, we propose a deep learning method that learns from the MR physics model without requiring the acquisition of any data to improve the fitting of mPC bSSFP qMT data. The training data was dynamically generated from the signal model, which allowed us to bypass the exhaustive collections of ground truth data while enabling the deep learning network to be supervised by MR physics. Experiments with digital phantom and in-vivo data demonstrated that the proposed method could reduce the noise in the estimation of qMT parameters and be more robust to measurement noise.

Methods

Preliminary
The signal equation of mPC-bSSFP-qMT was described in³
$$M=\frac{M_E(1-ae^{i\theta})}{1-bcos\theta}expi(\frac{\psi}{2}+\phi_{RF})$$
where the parameters M_E, a, and b depend on tissue relaxation times T_1f, T_2f, and qMT parameters k_f and F. Other relevant parameters such as T_1b, T_2b, on-resonance lineshape G(0) followed the assumption in previous works^3,11.

Proposed method
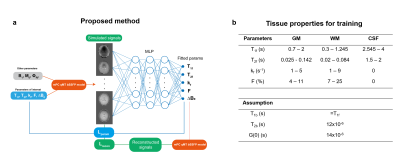
Figure 1a describes the overall scheme of our proposed physics-informed artificial neural network. During the training, the MR parameters of interest, T_1f, T_2f, k_f, F, were uniformly sampled from predefined ranges for each tissue (Figure 1b) and used to simulate MR signals for training. The network was a multiple-layer perceptron (MLP) that predicted the MR parameters corresponding to the simulated signal. Two losses were used to train the model: the mean squared error between ground truth and predicted parameters (L_param) and between input and reconstructed signals (L_recon).
We used an eight layers network with 512 hidden neurons in each layer. During training, 10000 batches of 8192 samples composed of roughly equal proportions of CSF, GM, and WM were selected per epoch, and the parameters corresponding to each tissue type were randomly drawn. Random Gaussian noise with SNR between [50, 100] was added to both the real and imaginary components of the simulated signals. The simulated complex signals were normalized by dividing by the mean magnitude of all acquisitions.

Experiments with simulation data
We compared the proposed method with the ellipse MT fitting method (EMT) by Wood et al³. Normalized root mean squared error (NRMSE) was used to quantify the accuracy of the fitting:
$$NRMSE(x_{fit},x_{GT})=\frac{1}{\overline{x_{GT}}}\sqrt{\frac{1}{N}\sum_{i}^{N}(x_{fit,i}-x_{GT,i})^2}$$
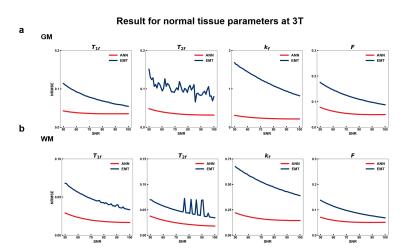
10 million data points, consisting of GM and WM's tissue properties at 3T from Stanisz et al⁵, were simulated with 50 SNR values in [50,100].
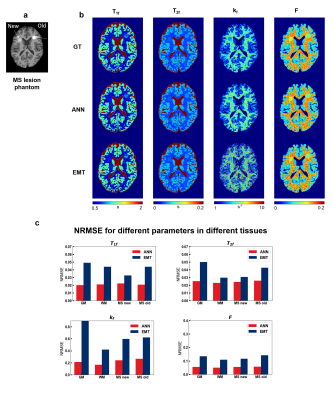
To evaluate the possibility of applying the methods to clinical pathologies, we additionally performed experiments on simulated brain with multiple sclerosis (MS) lesions. Brain phantom was obtained from the BrainWeb database^6-9,and two MS lesions (Figure 3a) were added. Parameters from MS patients at 1.5T were obtained from Sled¹¹ and simulated with an SNR of 70.

In-vivo experiments
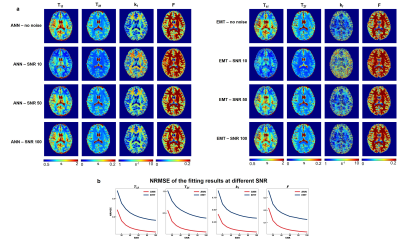
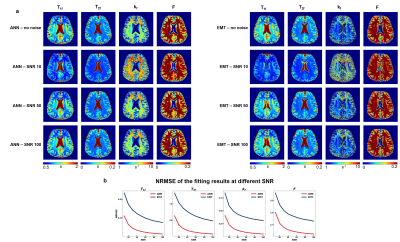
All experiments were approved by the local institutional review board with written consent from the participants. Data was acquired from 2 healthy volunteers with a Siemens Verio 3T scanner. Axial 3D bSSFP was scanned with a matrix size of 192×192×60 at a voxel size of 1.3×1.3×2.6 mm³. Following the previous protocol³, 24 bSSFP datasets were acquired with 2 flip angles (30°, 15°), 2 RF durations (0.5ms, 2ms), and 6 RF phase-cycling increments, resulting in a scan time of 31 minutes with 6/8 phase PF. To quantify the robustness of the fitting, Gaussian noises with 10 SNR values [10:10:100] were added to the acquired data, and the noisy data's fitting results were compared with those derived from data without the added noise.

Results

Figure 2 displayed the result of the first simulation experiment with the network fitting method (ANN) showing lower NRMSE value across all SNRs. For the brain with MS lesion phantom, ANN and EMT fitting methods produced results consistent with ground truth (Figure 3b). While the lesions were distinguishable from normal tissues with both methods, ANN showed less noisy k_f values and lower NRMSE across tissue types and parameters (Figure 3c). Figures 4 and 5 showed the fitting results for in-vivo data from subjects 1 and 2, respectively. T_1f and T_2f were fitted with good agreement between the two fitting methods, while the proposed method demonstrated improvement in fitting qMT parameters (Figures 4a and 5a). Figure 4b and 5b showed that the proposed method also exhibited more robustness against measurement noise, with consistently lower NRMSE across all levels of SNRs that include values outside the training data ranges.

Discussion and conclusion

The proposed physics-informed ANN-based fitting method demonstrated clear improvements over the conventional method while being more resilient against noises for both simulated and in-vivo data. Since the method is less influenced by SNR, it is beneficial to incorporate parallel imaging or reduce the number of scans to accelerate the data acquisition while still maintaining acceptable fitting results. Further optimization of the protocol with the proposed method has the potential to enable simultaneous qMT and relaxometry in the whole brain within a clinically reasonable scan time.

Acknowledgements

No acknowledgement found.