Synopsis

Keywords: CEST & MT, CEST & MT, Spin lock, CESL

The exchange weighting and robustness to B₀-inhomogeneities are essential properties for accurate CEST-MRI saturation measurements. Therefore, we investigated these properties for a new numerical optimized saturation pulse train and for state-of-the-art saturation pulse strategies in simulation and phantom measurements. We have found that the optimized pulse train generates superior CEST contrast and has very high stability against B₀-inhomogenities while maintaining the natural shape at the water peak which improves CEST-spectrum fitting and B₀-correction.

Introduction

Saturation pulses are an essential part of CEST-MRI measurements and are responsible for the quality of Z-spectra. Different kinds of saturation pulses have been developed during the past fulfilling different criteria and practical applicability. In a recent work using optimal control (OC), it was possible to design pulses that perform almost identical to the theoretical optimal continuous-wave saturation$$$^1$$$. For all saturation strategies the exchange weighting and robustness to $$$B_0$$$-inhomogeneities are essential properties$$$^{2-3}$$$. Therefore, these properties are analyzed for real-valued OC-pulses, and compared to classical Gaussian (G) and block pulse train (BPT) pulses, as well as recently developed saturation pulse strategies based on adiabatic Spin Lock (SL) pulses$$$^{4-6}$$$.

Methods

To test the performance of the different pulses, a $$$87$$$ $$$mM$$$ creatine monohydrate phantom is used in a $$$500$$$ $$$ml$$$ glass sphere. Relaxation times are reduced with Manganese(II)chloride to $$$T_1=~680$$$ $$$ms$$$, $$$T_2=~90$$$ $$$ms$$$. A phosphate buffer is used to maintain a pH of $$$7.4$$$. An air bubble is intentionally placed inside the sphere to introduce $$$B_0$$$-inhomogeneities leading to a resonance frequency shift of up to $$$200$$$ $$$Hz$$$.Z-spectra are measured for $$$\omega\in[-6,6]$$$ in steps of $$$0.1$$$ $$$ppm$$$. The readout is performed using a centric 2D-GRE with parameters: $$$FOV=160\times160$$$ $$$mm^2$$$, $$$\alpha=10^{\circ}$$$, $$$T_R=12$$$ $$$ms$$$ and $$$T_E=4$$$ $$$ms$$$, $$$resolution=64\times64$$$, one slice with thickness $$$5$$$ $$$mm$$$. To evaluate the exchange weighting of the different pulses, $$$MTR_{asym}$$$ $$$^7$$$, and a pixel-wise two-pool-Lorentzian fit with the MATLAB function \texttt{lsqcurvefit} are used. The measured data is $$$B_0$$$-corrected with the $$$B_0$$$-shift of the water peak received from the Lorentzian-fit. Furthermore, the CEST-images are TGV-denoised$$$^{8,9}$$$. The RF-magnitude of a $$$T_{sat}=1$$$ $$$s$$$, $$$DC=90\%$$$, pulse train is optimized by minimization of\begin{align*} &\underset{B_1}{\min}\, J(B_1,M_z,\tilde{M}_z)=\frac{\alpha}{2}\int\limits_{t=0}^{T_{sat}}B_1(t)^{2} dt+\frac{\beta}{p}\sum_{\omega}|M_z(\omega)-{M}_{zdes}(\omega)|^p+\frac{\gamma}{p}\sum_{\omega}|\tilde M_z(\omega)-\tilde{M}_{zdes}(\omega)|^p.\end{align*}$$$B_1$$$ is a free-form real-valued RF pulse. The second and third terms minimize the difference between the CEST-spectrum of the RF-pulse and a desired CW-CEST-spectrum of a Bloch-McConnell simulation with two pools$$$^{10}$$$. While $$$M_z(\omega),{M}_{zdes}(\omega)$$$ denote the spectra with the offresonances $$$\omega$$$ with two pools, $$$\tilde{M}_{zdes}(\omega),\tilde M_z(\omega)$$$ denote the spectra with one water pool. The metric for the differences is conducted via $$$L^p$$$-norm, $$$p>2$$$ even. $$$\alpha>0$$$ is the regularization parameter, $$$\beta,\gamma>0$$$ are penalization parameters. The RF-pulse is optimized using the hybrid semismooth quasi-Newton method$$$^{11}$$$, initialized with a BPT with constant phase. The details of the optimization are described in$$$^1$$$.The OC-pulse, an adiabatic SL-pulse, a BPT- and a Gaussian pulse-train are implemented via Pulseq-CEST$$$^12$$$ on a $$$3T$$$ Siemens Vida clinical scanner system. All pulses are investigated with a 20-channel head coil with a saturation time of $$$T_{sat}=1$$$ $$$s$$$, a $$$DC=90\%$$$ and $$$B_{1,RMS}=1$$$ $$$\mu$$$T. The adiabatic SL-pulse is taken directly from the Pulseq-CEST library. The adiabatic SL pulse was optimized for applications at $$$3$$$ $$$T$$$ by Kai Herz et al.$$$^4$$$

Results and Discussion

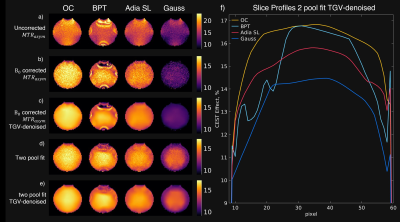
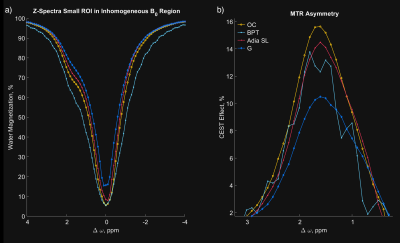
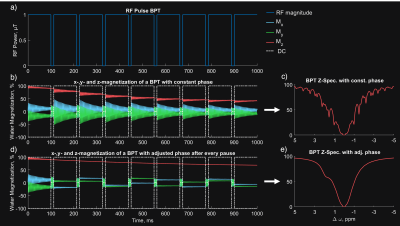
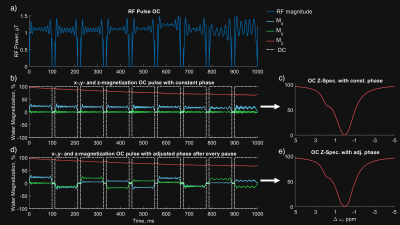
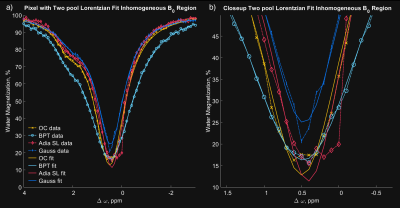
For each pulse Figure 1a shows the $$$MTR_{asym}$$$-image of the phantom at the creatine peak offset. Figure 1d shows the amplitude of the creatine peak in the pixel-wise two-pool-Lorentzian-fit. Figure 1c,e are the corresponding images TGV-denoised. The vertical slice profile Figure 1f through the inhomogeneous region of the fitted image shows that the OC-pulse yields the highest CEST-effect in every pixel. This can also be seen in the spectrum and $$$MTR_{asym}$$$-peak in Figure 2. Furthermore, the OC-pulse shows high robustness in the region of $$$B_0$$$-inhomogeneity which can be seen in Figure 1f from pixel 10 to 30.The implementation of the BPT is also important. BPTs are particularly susceptible to resonance-offsets if the phase of individual blocks is not continued ($$$\Delta p \omega_n B_0 \gamma$$$) according to the current frequency in the pulse pause (Figure 3 b,c), whereby $$$\Delta p$$$ is the pause length.It turns out that the OC pulse (Figure 4a) rotates the magnetization vector so that the magnetization vector ends in the z-direction after each block. Interestingly, this is the same concept as followed by the offresonant SL approach $$$^{14}$$$. The OC pulse shows this behavior for each offresonance (Figure 4b,d) and regardless of a shift in the starting phase (Figure 4c, d) making the pulse inherently $$$B_0$$$-robust (see Figure 4b,d).In particular, for the two-pool-Lorentz-fit results, the OC pulse shows high homogeneity. This is because the OC-pulse maintains a natural line shape, particularly in the inhomogeneous region. The fit in the inhomogeneous region can be seen in Figure 5a,b, where the adiabatic SL leads to an asymmetric water peak in the region around $$$0$$$ $$$ppm$$$ with $$$B_0$$$-inhomogeneities greater than $$$100$$$ $$$Hz$$$ as described by $$$^{5}$$$.

Conclusion

Overall, we have found that numerically optimized pulses generate the best CEST-contrast and have very high stability against $$$B_0$$$-inhomogenities. The adiabatic SL pulses follow afterwards and are also significantly better than conventional pulse trains. Furthermore, OC-pulses are able to maintain a natural shape at the water peak and exhibit high label efficiency in the presence of $$$B_0$$$-inhomogenities over $$$100$$$ $$$Hz$$$, which improves the fitting of the CEST spectrum and $$$B_0$$$-correction.

Acknowledgements

This research was funded in whole, or in part, by the Austrian Science Fund FWF-I4870.