Synopsis

Keywords: Image Reconstruction, Quantitative Susceptibility mapping

The SPICE technique has demonstrated a unique capability of simultaneous QSM/MRSI. To achieve fast high-resolution QSM, highly sparse sampling of (k,t)-space is used in SPICE data acquisition, which poses a significant challenge in image reconstruction. In this work, we solved this problem using a subspace-assisted parallel imaging technique with learned image priors. The proposed method has been validated using experimental data, producing high-quality QSM maps from the unsuppressed water signals of ¹H-MRSI scans.

Introduction

QSM and MRSI provide complementary information of brain tissues [1-2]. Recently, the SPICE technique has demonstrated a unique capability of simultaneous QSM/MRSI, by integrating fast ¹H-MRSI sequence, elimination of water suppression pulses, special sampling trajectories, and sparse sampling of (k,t)-space [3-5]. However, to achieve high-resolution QSM with fast imaging speed, SPICE samples peripheral k-space very sparsely in acquiring the unsuppressed water signals (around a factor of 36-fold undersampling). This poses a significant challenge for reconstruction of the water spectroscopic signals that are used for QSM.

In this work, we propose a subspace-assisted parallel imaging method to overcome this issue. The proposed method keeps the union-of-subspaces model, and further incorporates machine learning-generated spatial priors and localized temporal basis to provide stronger constraints to compensate the missing spatial encodings. The learned spatial priors contain high-resolution anatomical information obtained using deep learning-based translation of the MPRAGE anatomical image. Localized temporal basis functions were used to compensate for the limitation of the union-of-subspaces model. Both phantom and in vivo experiments were carried out to validate the proposed method, and the results showed that the proposed method could provide considerably improved reconstructions with less artifacts and clearer image details.

Method

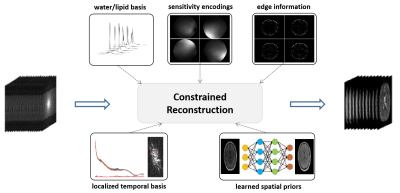
The proposed reconstruction integrates union-of-subspaces modeling, sensitivity encodings, edge information, pre-determined water/lipid basis and localized temporal basis, and machine learning-generated spatial priors to overcome the sparse sampling issue, as illustrated in Figure 1.

Union-of-Subspaces Model: With the union-of-subspaces model, the water unsuppressed ¹H-MRSI signals collected by SPICE can be represented as [3]:
$$\rho_{MRSI}\left(r,t\right)=\sum_{l_w=1}^{L_w}U_{l_w}\left(r\right)V_{l_w}\left(t\right)+\sum_{l_f=1}^{L_f}U_{l_f}\left(r\right)V_{l_f}\left(t\right)+\sum_{l_m=1}^{L_m}U_{l_m}\left(r\right)V_{l_m}\left(t\right) \ \ \ \ \ (1)$$
This union-of-subspaces model not only significantly reduces the degrees-of-freedom thus enabling high-quality reconstruction from highly sparse measurements, but also allows effective incorporation of various priors.

Determination of Basis Functions: The basis functions of water and lipid signals ($$$\{V_{l_f}\left(t\right)\}$$$ and $$$\{V_{l_w}\left(t\right)\}$$$) were determined in the same way as the original SPICE method [3]. The localized temporal basis for each reconstructed k-space temporal signals were estimated from its neighboring lines.

Learning of Spatial Priors: The spatial priors were generated using a pix2pix GAN to translate the contrast of MPRAGE images into the contrast of SPICE water images. The network was trained using 1708 MPRAGE-SPICE pairs.

Image Reconstruction: With these priors determined, the image reconstruction was performed in three steps:
(1). Initial reconstruction. The original reconstruction method using the union-of-subspaces model was used to generate the initial reconstruction results [5]: $$\left\{U_i\right\}=arg\min_{U_i}||d-\Omega_k\mathcal{F}\left(B\odot S\odot\left(\sum_{i=1}^IM_i\odot\left(U_iV_i\right)\right)\right)||_2^2+\lambda||\sum_{i=1}^IWU_i||_2^2 \ \ \ \ (2)$$where $$$\Omega_k$$$, $$$\mathcal{F}$$$, $$$B$$$, $$$S$$$, $$$W$$$, $$$M_i$$$, $$$V_i$$$, $$$U_i$$$ denote sampling in (k, t)-space, Fourier encoding, field map, sensitivity map, edge weights, spatial boundaries, temporal basis, and corresponding spatial coefficients, respectively.
(2). Subspace-assisted GRAPPA reconstruction. The reconstructed (k, t)-data in temporal direction were kept but the reconstructed spatial data in ky direction were discarded. GRAPPA [7] was used to recover the remaining undersampled measurements (with only a factor of 3). It was performed with a time-dependent manner in consideration of the rich contrast variations among the large number of echoes acquired by the SPICE sequence. Then, each reconstructed k-space temporal signal was projected onto its pre-determined temporal basis to utilize the position-dependent local correlations. The reconstruction results in this step are assigned as the label of neural network-based image translation.
(3). Final reconstruction using learned spatial priors. The final reconstruction was performed by solving the following optimization problem: $$\left\{U_i\right\}=arg\min_{U_i}||d-\Omega_k\mathcal{F}\left(B\odot S\odot\left(\sum_{i=1}^IM_i\odot\left(U_iV_i\right)\right)\right)||_2^2+\lambda_1||\sum_{i=1}^IWU_i||_2^2+\lambda_2||\sum_{i=1}^IM_i\odot\left(U_iV_i\right)-\rho_{NN}||_2^2\ \ \ \ (3)$$where $$$\rho_{NN}$$$ denotes the learned spatial prior via neural network-based image translation. The second term is an edge-preserving regularization, while the third term tends to pursuit of more abundant spatial anatomy.

Results

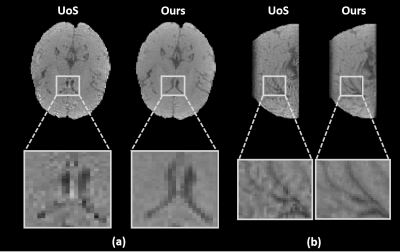
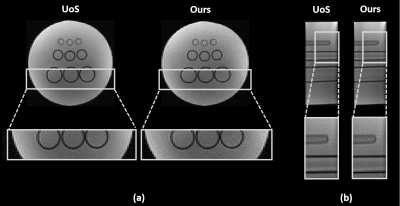
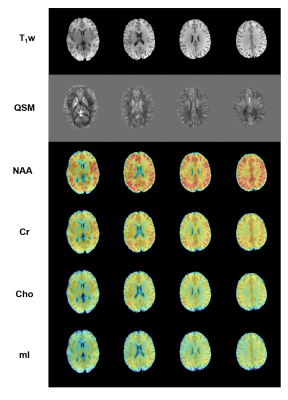
To demonstrate the feasibility of the proposed method, both in vivo and phantom experiments were carried out on a 3T scanner (MAGNETOM Prisma, Siemens Healthcare, Erlangen, Germany). Figure 2 shows a set of representative water reconstruction results from the proposed method in comparison with the union-of-subspaces (UoS) model. Both coronal and sagittal sections illustrate that the proposed method obtained improved water reconstruction with fewer artifacts and clearer anatomy. The phantom image reconstructed by our method has better resolution with sharper edges as shown in Figure 3. The results of higher resolution QSM (with nominal spatial resolution of 1.0×1.0×2.0 mm³) brought by improved water reconstruction can be found in Figure 4. Microstructures of the brain like veins can be clearly seen in the proposed method but not in the UoS model-based method. The simultaneously acquired metabolite maps (with nominal spatial resolution of 2.0×3.0×3.0 mm³) are shown in Figure 5. As can be seen, high-resolution and high-quality spatiospectral distributions of metabolites have been obtained successfully. These experimental results confirm the feasibility of our proposed method in obtaining high-resolution QSM for simultaneous QSM/MRSI experiments.

Conclusion

We present an improved method to achieve high-resolution QSM for simultaneous QSM/MRSI experiments. The proposed method uses a subspace-assisted parallel imaging technique with learned image priors to solve the problem of image reconstruction from highly sparse data. The proposed method has been validated using experimental data, producing high-quality QSM maps from the unsuppressed water signals of ¹H-MRSI scans.

Acknowledgements

This work was supported by Shanghai Pilot Program for Basic Research—ShanghaiJiao Tong University (21TQ1400203); the National Natural Science Foundation of China (81871083); and Key Program of Multidisciplinary Cross Research Foundation of Shanghai Jiao Tong University (YG2021ZD28).