Synopsis

Keywords: Image Reconstruction, Spectroscopy

A computationally efficient MRSI reconstruction method is presented. The proposed problem formulation integrates a subspace model of the high-dimensional spatiotemporal function (SPICE) and a network-based learned projector on to a low-dimensional manifold of generic spectroscopic signals. The subspace representation allows for more flexible spatiotemporal sampling designs than using nonlinear manifold constraint alone, while the manifold constraint effectively regularizes the subspace fitting, especially at higher orders. An efficient algorithm is designed to solve the optimization problem. The benefits of the proposed synergy have been demonstrated using simulations as well as experimental ³¹P and ¹H-MRSI data.

Introduction

Subspace imaging methods have demonstrated significantly improved tradeoffs in speed, resolution, and SNR for various MRSI applications^1-8. Besides reducing the number of degrees-of-freedom, subspace models also allow for flexible temporal sampling (e.g., acquiring truncated or subNyquist FIDs for acceleration or rapid spatiospectral encoding), as the basis determines the spectral resolution (unlike the standard Fourier transform). Meanwhile, model order selection remains challenging. One solution is to choose a relaxed higher order for better model accuracy which increases the number of unknowns and worsens the conditioning of the fitting problem^9,10. Recently, more efficient neural network (NN) based nonlinear low-dimensional models have shown great potential in improving MRSI reconstruction, e.g., the RAIISE method (joint leaRning of nonlineAr representatIon and projectIon for faSt constrained MRSI rEconstruction)⁹. However, this approach does not afford as flexible FID sampling design as subspace fitting. Here, we propose a novel method that integrates subspace modeling and nonlinear manifold-based regularization via a unified formulation, taking the advantage of both methods. A highly efficient algorithm leveraging ADMM and an NN-based learned manifold projector was developed to solve the associated optimization problem. We have evaluated our method using simulations as well as in vivo ³¹P-MRSI and ¹H-MRSI data. High-fidelity, high-SNR reconstructions from noisy MRSI data can be produced with flexible FID sampling designs, demonstrating the proposed method's advantages over subspace or manifold model alone.

Theory: Problem Formulation and Algorithm

The key ingredients in the proposed method are: (1) A predetermined linear subspace to model the high-dimensional spatiotemporal/spatiospectral function (see^1-8 for extensive discussion on subspace estimation); (2) Jointly learned NN-based nonlinear manifold of spectroscopic signals and a projector to recover the low-dimensional embeddings from noisy FIDs; and (3) A formulation combining (1) and (2). Specifically, we formulate the reconstruction as:$$\min_\mathbf{U,z}\|\mathbf{d}-\mathcal{F}_{\Omega}\{\mathbf{B}\odot\mathbf{UV}\}\|_2^2+\lambda R(\mathbf{UV})\quad(1)\\s.t.\mathbf{UV}=D(\mathbf{z}),$$where $$$\mathbf{UV}$$$ is the subspace model ($$$\mathbf{V}$$$ containing the basis), $$$\mathbf{d}$$$ the $$$(k,t)$$$-space data, $$$\mathcal{F}_{\Omega}$$$ an encoding operator with $$$(k,t)$$$-sampling pattern $$$\Omega$$$, $$$\mathbf{B}$$$ models the B₀ inhomogeneity, and $$$R(.)$$$ imposes complementary spatial regularization with parameter $$$\lambda$$$, e.g., $$$R(\mathbf{UV})=\|\mathbf{D}_w\mathbf{UV}\|_2$$$¹. The constraint $$$\mathbf{UV}=D(\mathbf{z})$$$ enforces the prior that the underlying spectroscopic signal should yield a low-dimensional manifold embedding $$$\mathbf{z}$$$. $$$D(.)$$$ is a learned decoder/generator as part of the learned NN model (i.e., complex-valued autoencoder as described in the RAIISE method⁹). Note that the subspace model order can be higher (more accurate) with the nonlinear manifold regularization.
An ADMM-based algorithm was used to solve Eq. (1). The augmented Lagrangian function is:$$\boldsymbol{L}(\mathbf{U},\mathbf{z},\mathbf{Y})=\|\mathbf{d}-\mathcal{F}_{\Omega}\{\mathbf{B}\odot\mathbf{UV}\}\|_2^2+\lambda R(\mathbf{UV})+\frac{\mu}{2}\|\mathbf{UV}-D(\mathbf{z})+\frac{\mathbf{Y}}{\mu}\|_{F}^2,$$where $$$\mathbf{Y}$$$ is the Lagrangian multiplier. The following three subproblems were solved iteratively ($$$i$$$ being the iteration index):
Subproblem (I): Update $$$\mathbf{U}$$$$$\mathbf{U}^{(i+1)}=\min_{\mathbf{U}}\|\mathbf{d}-\mathcal{F}_{\Omega}\{\mathbf{B}\odot\mathbf{UV}\}\|_2^2+\lambda R(\mathbf{UV})+\frac{\mu}{2}\|\mathbf{UV}-D(\mathbf{z}^{(i)})+\frac{\mathbf{Y}^{(i)}}{\mu}\|_{F}^2,$$which is the subspace fitting in SPICE with an additional regularization term.
Subproblem (II): Update $$$\mathbf{z}$$$$$\mathbf{z}^{(i+1)}=\min_{\mathbf{z}}\frac{\mu}{2}\|\mathbf{U}^{(i+1)}\mathbf{V}-D(\mathbf{z})+\frac{\mathbf{Y}^{(i)}}{\mu}\|_{F}^2.$$
Directly solving this problem requires time-consuming backpropagation. Thus, we adapted the learned projection concept in RAIISE and reformulated subproblem (II) as:$$\mathbf{z}^{(i+1)}=\min_{\mathbf{z}}\frac{\mu}{2}\|P(\mathbf{U}^{(i+1)}\mathbf{V}+\frac{\mathbf{Y}^{(i)}}{\mu})-\mathbf{z}\|_{F}^2,$$where $$$P(.)$$$ is the learned manifold projector with $$$P(D(\mathbf{z}))=\mathbf{z}$$$.
Subproblem (III): Update $$$\mathbf{Y}$$$$$\mathbf{Y}^{(i+1)}=\mathbf{Y}^{(i)}+\mu(\mathbf{U}^{(i+1)}\mathbf{V}-D(\mathbf{z}^{(i+1)}))$$

Methods

The proposed method was evaluated using simulations and experimental data. For simulation, a ³¹P phantom was generated with a lesion-mimicking feature and noise added to $$$(k,t)$$$-space data (details in¹⁰).
In vivo ³¹P-MRSI data were acquired from a healthy volunteer on a Siemens Magnetom 9.4T system with: TR/TE = 250/1.3 ms, FOV = 180$$$\times$$$200$$$\times$$$180 mm³, matrix size = 28$$$\times$$$30$$$\times$$$13, spectral BW = 5000 Hz and 512 FID points¹¹. The reconstruction used the first 256 points with $$$\times$$$2 undersampling (128 points in total) to demonstrate the ability of flexible sampling. ¹H-MRSI data were acquired from a post-traumatic epilepsy (PTE) patient on a Prisma 3T system using a 3D-EPSI sequence: TR/TE = 1000/65 ms, FOV = 220$$$\times$$$220$$$\times$$$64 mm³, matrix size = 42$$$\times$$$42$$$\times$$$8, spectral BW = 1087 Hz and 200 FID points. Reconstruction was performed at 512-pt FID length for a higher spectral resolution. All in vivo studies were IRB-approved.

Results

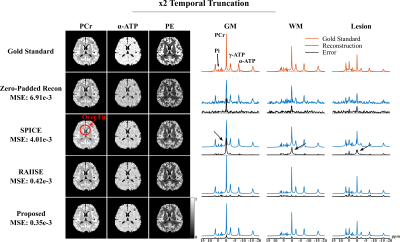
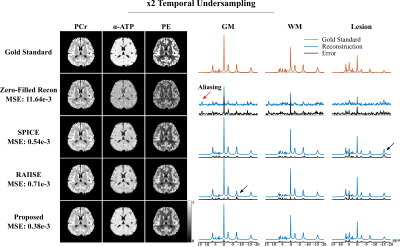
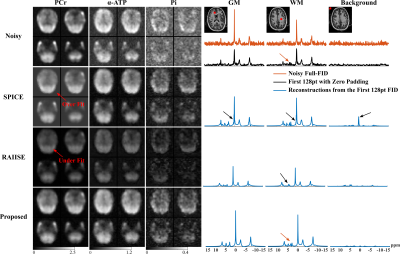
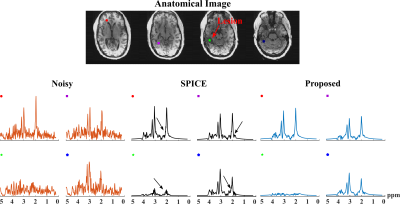
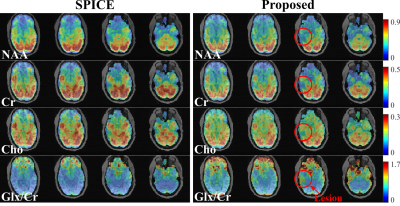
For simulation, we compared the proposed method with reconstructions using subspace (SPICE, model order 26 with 5% truncation error) or nonlinear manifold constraints (RAIISE) alone, from both temporally truncated (Fig. 1) and undersampled (Fig. 2) FIDs (shorter FID for SNR or shorter TRs, and undersampled FID mimicking EPSI acquisitions with large echo spacings due to gradient limits). As can be seen, SPICE-based reconstruction with a higher model order tends to overfit for truncated FIDs (Fig. 1), while the performance of RAIISE deteriorates substantially for undersampled data (Fig. 2). The proposed method produced the best reconstruction in both scenarios quantitatively (with MSE) and qualitatively, demonstrating its robustness for various sampling choices. In vivo ³¹P-MRSI reconstruction ($$$\times$$$2 truncation and $$$\times$$$2 undersampling) are shown in Fig. 3. Similarly, we can observe that both high order subspace and RAIISE yielded degraded reconstructions with over/under fitting issues, while the proposed method consistently achieved high-fidelity, high SNR reconstruction (Fig. 3; orange arrows indicating better-preserved spectral features revealed by truncated FIDs). Figures 4 and 5 show ¹H-MRSI reconstruction from a PTE patient. The proposed method produced again better-quality spectra (Fig. 4) and tissue contrast with better lesion delineation (Fig. 5).

Summary

A novel MRSI reconstruction method that combines linear and nonlinear models was developed. Improved reconstructions from simulation and in vivo data with different FID sampling designs demonstrate the advantages of the proposed method and its potential for accelerated acquisitions.

Acknowledgements

This work was supported in part by NSF-CBET-1944249 and NIH-NIBIB-1R21EB029076A