0863

Investigations on non-Cartesian parallel imaging with time-varying receive sensitivities

Felix Glang¹, Praveen Iyyappan Valsala¹, Anton V. Nikulin^1,2, Nikolai Avdievich¹, Theodor Steffen¹, and Klaus Scheffler^1,2
¹High-field Magnetic Resonance Center, Max Planck Institute for Biological Cybernetics, Tübingen, Germany, ²Department of Biomedical Magnetic Resonance, Eberhard Karls University Tübingen, Tübingen, Germany

Synopsis

Keywords: Parallel Imaging, High-Field MRI

Non-Cartesian trajectories have several advantageous properties, including favorable parallel imaging performance. Recently, a novel concept of improving parallel imaging by electronically modulated time-varying receive sensitivities has been introduced. In the present work, we investigate if these two concepts can be combined, i.e., how dynamic sensitivity modulation impacts non-Cartesian parallel imaging reconstruction. To that end, numerical experiments are performed based on data from the novel reconfigurable coil array. We find improvement in convergence, reconstruction error and noise amplification due to rapid sensitivity modulation for radial, spiral, and Cartesian trajectories, implying the potential of this method for advanced encoding and reconstruction schemes.

Introduction

Non-Cartesian k-space trajectories like radial or spiral offer multiple benefits over conventional Cartesian sampling, like using the gradient hardware more efficiently for faster image encoding, being less sensitive to motion, or enabling ultra-short TE imaging. In addition, combining non-Cartesian trajectories with parallel imaging (PI) has been reported beneficial when compared to Cartesian PI¹.
Recently, it has been demonstrated that time-varying coil sensitivities enabled by a novel receive array at 9.4T can improve Cartesian PI performance². Here we investigate whether this additional degree of freedom can also be useful for non-Cartesian image reconstruction. Employing a modified CG SENSE³ formulation, condition numbers of encoding operators, reconstruction errors and g-factors for multiple trajectories, acceleration factors and sensitivity switching patterns are evaluated.

Methods

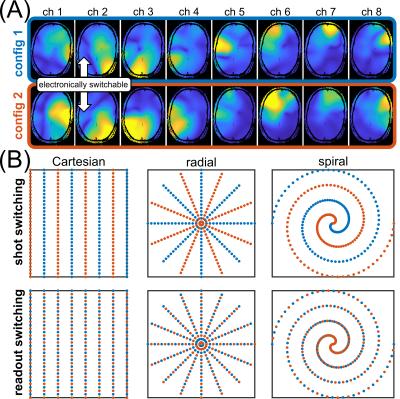
Switchable sensitivity maps (Figure 1A) were acquired on a 9.4T human whole-body MR scanner (Siemens Healthineers, Erlangen, Germany), using the previously introduced reconfigurable receive loop array².
We describe non-Cartesian parallel imaging with time-varying sensitivities by a modified SENSE model^2,4,5, according to the signal equation $$$\mathbf{s}=\mathbf{E}\mathbf{m}$$$ with the acquired multi-channel data $$$\mathbf{s}$$$, the image $$$\mathbf{m}$$$ and the encoding operator
$$\mathbf{E}_{(\beta,\kappa),\rho} = c_\beta(\mathbf{r}_\rho, t_\kappa) \, \exp\left(\text{i} \mathbf{k}(t_\kappa)\cdot\mathbf{r}_\rho\right) \quad[1],$$ which consists of the time-varying sensitivities $$$c_\beta$$$ at locations $$$\mathbf{r}_\rho$$$ and time points $$$t_\kappa$$$, and Fourier terms according to the k-space trajectory $$$\mathbf{k}$$$. Reconstructions can be obtained iteratively by the CG algorithm applied to the normal equations $$$\mathbf{E}^H \mathbf{Em}=\mathbf{E}^H \mathbf{s}$$$, decomposing $$$\mathbf{E}$$$ into efficient operations without the need to store large matrices in memory, in particular using density-compensated NUFFT^3,6,7. Previously acquired Cartesian data was interpolated onto multi-shot radial and Archimedean spiral trajectories to enable retrospective reconstruction experiments (image matrix 256x256). Complex Gaussian noise of 0.1% of the maximum signal was added to mimic a more realistic acquisition. Spiral trajectories with [32,33,32,30,30] interleaves (Nyquist-sampled) were used for acceleration factors R=[2,3,4,5,6] to guarantee divisibility when omitting interleaves. Reconstructions at each CG iteration were assessed via the relative iteration residual
$$\delta_i = \frac{||\mathbf{E}^H \mathbf{Em}_i-\mathbf{E}^H \mathbf{s}||_2}{||\mathbf{E}^H \mathbf{s}||_2} \quad [2]$$
and reconstruction error
$$\Delta_i = \frac{||\mathbf{m}_{\text{true}} - \mathbf{m_i}||_2}{||\mathbf{m}_{\text{true}}||_2} \quad [3]$$
with a fully-sampled ground-truth reconstruction $$$\mathbf{m}_{\text{true}}$$$. Condition numbers were evaluated as the ratio of largest to smallest singular value of $$$\mathbf{E}$$$ (on a downsampled 96x96 grid to keep computation tractable). G-factors were calculated via the pseudo-multiple replica method^8,9,10.

Results

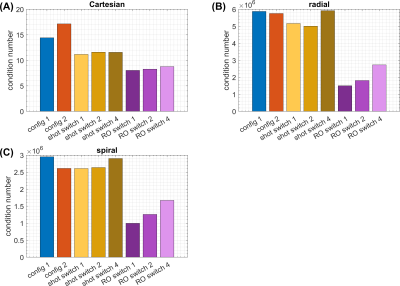
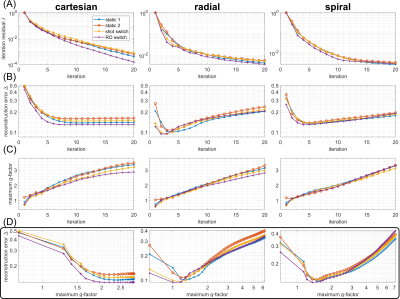
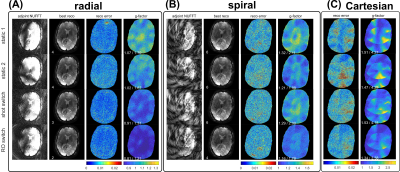
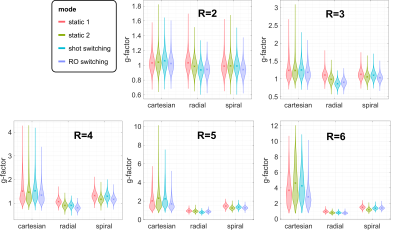
Condition numbers are generally much higher for non-Cartesian (Figure 2B,C,D) than for Cartesian trajectories (Figure 2A), which can be attributed to the non-uniform k-space coverage and lack of support in the outer k-space corners^3,11. For all trajectories, switching fast during readout (“RO switch 1”, Figure 1B) yields the strongest reduction of condition number compared to conventional static sensitivities, while switching slower (“RO switch 2/4”) helps less. Shot switching improves conditioning for radial and Cartesian trajectories (Figure 2B).
Analysis of the CG convergence behavior reveals that RO switching enables faster convergence than static sensitivities for all trajectories, both with respect to relative residual $$$\delta$$$ (Figure 3A) as well as absolute reconstruction error $$$\Delta$$$ (Figure 4B). For radial, the same holds true for shot switching, in accordance with the condition numbers (Figure 2B). All non-Cartesian trajectories show the known semi-convergence of CG¹¹, i.e., increase of $$$\Delta$$$ for a larger number of iterations beyond a certain optimum. In all cases, increasing number of iterations leads to increased noise amplification (Figure 3C). Non-Cartesian trajectories and readout switching enable a more favorable combination of low g-factors and reconstruction error when terminated optimally, compared to Cartesian and non-switching (Figure 3D). This is confirmed by the g-factors obtained at the respective optimum iteration for multiple acceleration factors (Figure 5). Exemplary images and g-factor maps are shown in Figure 4. Note that the observed g-factors below 1 for radial indicate a denoising effect of early-stopped CG, which effectively acts as regularization and comes at the cost of slight blurring.

Discussion

Exemplarily for R=4, we found an improvement of maximum g-factor of (-21%,-28%,-10%) for (Cartesian, radial, spiral) due to fast RO switching compared to conventional static sensitivities, respectively. Overall, the obtained results indicate that radial trajectories might be particularly suited for being combined with time-varying sensitivities. Evaluating g-factors at lowest reconstruction error $$$\Delta$$$ is not possible when fully sampled ground truth is not available, and serves here only as a theoretical metric for encoding capability. However, the observed faster convergence with respect to residual $$$\delta$$$ when switching might help achieving lower errors in a more realistic setting as well.
The present work focused only on CG SENSE reconstruction, which needs explicit sensitivity extraction in image space. Extending the concept of switching sensitivities to other reconstruction algorithms like non-Cartesian GRAPPA^12,13 or SPIRIT¹⁴ is conceivable and might reveal additional interesting interactions between switching and reconstruction.
Ultimate-intrinsic-SNR theory shows that for non-Cartesian sampling, theoretically there is a different optimal set of coil sensitivities for each k-space point¹⁵. Speculative future work might thus be to develop new reconfigurable coils dedicated for optimized switching combined with certain trajectories, or even joint optimization of receive hardware, trajectories and switching patterns.

Conclusion

Similar to previous findings in Cartesian parallel imaging, rapid sensitivity modulation has the potential to improve parallel imaging performance for non-Cartesian trajectories. Additionally, radial trajectories might also benefit from different (i.e., slower and thus easier to realize) switching patterns.

Acknowledgements

Financial support of the Max-Planck-Society, ERC Advanced Grant “SpreadMRI”, No 834940 and DFG Grant SCHE 658/12 is gratefully acknowledged.

References

1. Wright KL, Hamilton JI, Griswold MA, Gulani V, Seiberlich N. Non-Cartesian parallel imaging reconstruction. Journal of Magnetic Resonance Imaging 2014;40:1022–1040 doi: 10.1002/jmri.24521.

2. Glang F, Nikulin AV, Bause J, et al. Accelerated MRI at 9.4 T with electronically modulated time-varying receive sensitivities. Magnetic Resonance in Medicine 2022;88:742–756 doi: 10.1002/mrm.29245.

3. Pruessmann KP, Weiger M, Börnert P, Boesiger P. Advances in sensitivity encoding with arbitrary k-space trajectories. Magnetic Resonance in Medicine 2001;46:638–651 doi: 10.1002/mrm.1241.

4. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: Sensitivity encoding for fast MRI. Magnetic Resonance in Medicine 1999;42:952–962 doi: 10.1002/(SICI)1522-2594(199911)42:5<952::AID-MRM16>3.0.CO;2-S.

5. Trakic A, Wang H, Weber E, et al. Image reconstructions with the rotating RF coil. Journal of Magnetic Resonance 2009;201:186–198 doi: 10.1016/j.jmr.2009.09.009.

6. Fessler JA, Sutton BP. Nonuniform fast Fourier transforms using min-max interpolation. IEEE Transactions on Signal Processing 2003;51:560–574 doi: 10.1109/TSP.2002.807005.

7. Fessler JA. Michigan Image Reconstruction Toolbox. https://github.com/JeffFessler/mirt

8. Akcakaya M, Basha TA, Manning WJ, Nezafat R. Efficient calculation of g-factors for CG-SENSE in high dimensions: noise amplification in random undersampling. J Cardiovasc Magn Reson 2014;16:W28 doi: 10.1186/1532-429X-16-S1-W28.

9. Robson PM, Grant AK, Madhuranthakam AJ, Lattanzi R, Sodickson DK, McKenzie CA. Comprehensive quantification of signal-to-noise ratio and g-factor for image-based and k-space-based parallel imaging reconstructions. Magnetic Resonance in Medicine 2008;60:895–907 doi: 10.1002/mrm.21728.

10. Eggers H, Mazurkewitz P, Boesiger P. Noise Amplification in Non-Cartesian Parallel Imaging. Proc. Intl. Soc. Mag. Reson. Med. 13 (2005); 2429

11. Qu P, Zhong K, Zhang B, Wang J, Shen GX. Convergence behavior of iterative SENSE reconstruction with non-Cartesian trajectories. Magnetic Resonance in Medicine 2005;54:1040–1045 doi: 10.1002/mrm.20648.

12. Heidemann RM, Griswold MA, Seiberlich N, et al. Direct parallel image reconstructions for spiral trajectories using GRAPPA. Magnetic Resonance in Medicine 2006;56:317–326 doi: 10.1002/mrm.20951.

13. Seiberlich N, Ehses P, Duerk J, Gilkeson R, Griswold M. Improved radial GRAPPA calibration for real-time free-breathing cardiac imaging. Magnetic Resonance in Medicine 2011;65:492–505 doi: 10.1002/mrm.22618.

14. Lustig M, Pauly JM. SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space. Magnetic Resonance in Medicine 2010;64:457–471 doi: 10.1002/mrm.22428.

15. Ohliger MA, Grant AK, Sodickson DK. Ultimate intrinsic signal-to-noise ratio for parallel MRI: Electromagnetic field considerations. Magnetic Resonance in Medicine 2003;50:1018–1030 doi: 10.1002/mrm.10597.

Figures

Figure 1: (A) Examples of switchable sensitivity maps obtained from the receive array demonstrated previously². Sensitivities of config1 and config2 can be electronically switched within µs during k-space acquisition, which provides a novel degree of freedom for image encoding. (B) Investigated trajectories and sensitivity switching patterns. Colors indicate the respective sensitivity configuration applied at a particular k-space location. Sensitivities can be switched between RF excitations (“shot switching”) or rapidly between ADC samples (“readout switching”).

Figure 2: Condition numbers of the encoding operator (Eq. 1) for the case of (A) Cartesian, (B) radial, and (C) spiral trajectories. Multiple sensitivity switching patterns are indicated by labels: config 1 and config 2 are the cases of static sensitivities only (conventional parallel imaging), “shot switch 1/2/4” means switching for every / every second / every fourth excitation and “RO switch 1/2/4” means switching between every / every second / every fourth ADC sample during readout (cf. Figure 1). Results are shown for acceleration R=4.

Figure 3: Convergence behavior over the iterations of CG SENSE (R=4) for different trajectories and switching patterns measured by (A) CG iteration residual (Eq. 2), (B) reconstruction error with respect to the fully sampled ground-truth (Eq. 3), and (C) the maximum g-factor. (D) Reconstruction errors plotted against the respective maximum g-factor at each iteration to visualize the best achievable trade-off between reconstruction accuracy and noise amplification for a given encoding scheme. In these plots, the bottom left corner is the most favorable region.

Figure 4: Reconstruction results for accelerated (R=4) (A) radial and (B) spiral trajectories and different switching modes (rows). Shown are an adjoint NUFFT reconstruction (first column), the CG SENSE results with lowest reconstruction error (second column; iteration number displayed at the bottom left), maps of the reconstruction error (third column) and g-factor for the same iteration (fourth column; numbers indicate mean/max). (C) Corresponding reconstruction errors and g-factors for Cartesian sampling (R=4) as a reference.

Figure 5: Violin plots of g-factors for multiple acceleration factors R, trajectories and switching patterns. G-factors were evaluated for the iteration that resulted in lowest reconstruction error $$$\Delta$$$ for each individual case, representing the theoretical optimal termination point of CG SENSE.

Proc. Intl. Soc. Mag. Reson. Med. 31 (2023)

0863

DOI: https://doi.org/10.58530/2023/0863