0862
Robust Image Reconstruction using Multi-channel Spatial Nulling Maps: An Alternative to ESPIRiT?1Laboratory of Biomedical Imaging and Signal Processing, The University of Hong Kong, Hong Kong, Hong Kong, 2Department of Electrical and Electronic Engineering, The University of Hong Kong, Hong Kong, Hong Kong, 3Department of Electrical and Electronic Engineering, Southern University of Science and Technology, Shenzhen, China
Synopsis
Keywords: Signal Representations, Parallel Imaging
We develop a novel parallel imaging reconstruction method by extracting null-subspace bases of calibration data/matrix to calculate image-domain spatial nulling maps that contain both coil sensitivity and finite image support information. Images are reconstructed by solving a nulling system formed by multi-channel spatial nulling maps without any masking-related procedure (i.e., in existing SENSE/ESPIRiT for minimizing noise propagation). We demonstrate this method with 2D brain, knee and cardiac data under various conditions, yielding results highly comparable to ESPIRiT with optimal manual masking. Our proposed hybrid-domain reconstruction method is efficient, and more robust than existing ESPIRiT for parallel imaging in practice.Introduction
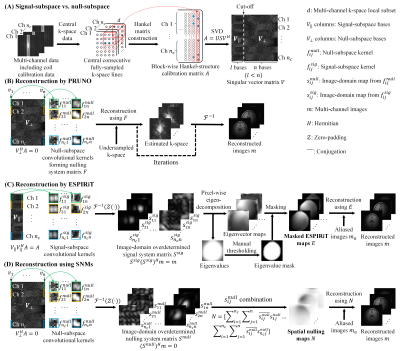
Existing parallel imaging reconstruction techniques generally fall into three classes: image-domain1-5, k-space6-17, and hybrid-domain category18. The image-domain methods such as SENSE1 utilize explicit knowledge of the coil sensitivity maps (CSMs). PRUNO13 is a k-space reconstruction method where a k-space nulling system is derived using null-subspace bases of the calibration matrix. It produces fewer residual artifacts with limited autocalibration signal when compared with GRAPPA13, but incurs high computational burden18. ESPIRiT18 reconstruction extends the PRUNO subspace concept by exploiting the linear relationship between signal-subspace bases and spatial coil sensitivity characteristics, yielding a hybrid-domain approach. Yet it requires empirical eigenvalue thresholding to mask the coil sensitivity information to minimize noise amplification during reconstruction.In this study, we combine the concepts of PRUNO and ESPIRiT to present a new hybrid-domain-based reconstruction method. It extracts null-subspace bases of the calibration matrix from k-space coil calibration data, and utilizes them to derive image-domain spatial nulling maps. The subsequent image reconstruction relies on solving the nulling system formed by spatial nulling maps without any masking-related procedure.
Theory and Experiments
The proposed method is illustrated in Figure 1 with comparison to PRUNO and ESPIRiT. First, the central consecutive fully-sampled k-space lines or coil calibration data are used to construct a block-wise Hankel-structure calibration matrix, in which the column entries exhibit strong linear dependencies6,13,14,18 (Figure 1A). By performing SVD, the singular vector matrix V with signal/null-subspace bases of A can be obtained:$$A=USV^H\tag{1}$$
where $$$V^H$$$ represents the Hermitian matrix of $$$V$$$. By setting a cut-off, the signal-subspace $$$V_{\|}$$$ and null-subspace $$$V_{\perp}$$$ are separated. Assuming that the two subspaces are ideally separated, two constraints are satisfied:
$$V_{\|\mid}V_{\|}^HA=A\text{ and}\tag{2}$$
$$V_{\perp}^HA=0.\tag{3}$$
With $$$V_{\perp}$$$, the segment corresponding to the $$$i$$$th channel of each null-subspace basis $$$v_j$$$ is transformed into a 2D null-subspace convolution kernel $$$f_{ij}^{\text{null}}$$$ through devectorization. According to Equation (3), a convolutional nulling relation between $$$f_{ij}^{\text{null}}$$$ and multi-channel k-space can be established:
$$\sum_{i=1}^{n_{c}}f_{ij}^{\text{null}}*k_{i}=0,j=1,\ldots,n\tag{4}$$
where $$$k_{i}$$$ denotes the k-space data from the $$$i$$$th channel. In contrast to PRUNO, each k-space kernel $$$f_{ij}^{\text {null}}$$$ is transformed into an image-domain map $$$s_{ij}^{\text{null}}$$$ through zero-padding and IFFT:
$$s_{ij}^{\text{null}}=\mathcal{F}^{-1}\left(Z\left(f_{ij}^{\text{null}}\right)\right),i=1,\ldots,n_{c};j=1,\ldots,n.\tag{5}$$
Using $$$s_{ij}^{\text {null}}$$$, an image-domain overdetermined nulling system can be formed:
$$\left(S^{\text{null}}\right)^{H}m=0,\quad\text{where }S^{\text{null}}=\left[\begin{array}{ccc}s_{11}^{\text{null}}&\cdots&s_{1n}^{\text{null}}\\\vdots&\ddots&\vdots\\s_{n_{c}1}^{\text{null}}&\cdots&s_{n_{c}n}^{\text{null}}\end{array}\right]\text{.}\tag{6}$$
Here $$$S^{\text{null}}$$$ is a large 2D overdetermined nulling system matrix and $$$m$$$ multi-channel images. Instead of solving the overdetermined system in Equation (6) for image reconstruction, multiple $$$s_{i j}^{\text {null }}$$$ are combined to construct multi-channel spatial nulling maps $$$N$$$:
$$N=\left[\sum_{i=1}^{n_{c}}\sum_{j=1}^{n}\overline{s_{ij}^{\text{null}}}s_{1j}^{\text{null}}\mspace{10mu}\sum_{i=1}^{n_{c}}\sum_{j=1}^{n}\overline{s_{ij}^{\text{null}}}s_{2j}^{\text{null}}\ldots\mspace{10mu}\sum_{i=1}^{n_{c}}\sum_{j=1}^{n}\overline{s_{ij}^{\text{null}}}s_{n_{c}j}^{\text{null}}\right],\tag{7}$$
where $$$\overline{s_{ij}^{\text{null }}}$$$ denotes the conjugation of $$$s_{ij}^{\text{null }}$$$. With $$$N$$$, an image-domain nulling system can be built:
$$Nm=0.\tag{8}$$
Here $$$m$$$ can be further represented as $$$m=m_{a}+m_{m}$$$, where $$$m_{a}$$$ are aliased multi-channel images reconstructed from undersampled k-space and $$$m_{m}$$$ the multi-channel images corresponding to underlying missing k-space. Therefore, the image-domain nulling system in Equation (8) becomes:
$$N\left(m_{a}+m_{m}\right)=0.\tag{9}$$
The multi-channel images $$$m$$$ (i.e. $$$m_{a}+m_{m}$$$) can then be reconstructed by solving this nulling system. Specifically, with spatial nulling maps N estimated from central k-space lines, a least-square solution of $$$m_{m}$$$ in Equation (9) can be calculated19:
$$\widehat{m}_{m}=\arg\min_{m_{m}}\left\|N\left(m_{a}+m_{m}\right)\right\|_{2}^{2}\tag{10}$$
For evaluation, public MR datasets were used to evaluate our proposed method, including 3T T1W GRE brain data (12-channel, TR/TE/TI=6.3/2.6/400ms) from Calgary-Campinas database20, 1.5T PDW FSE knee data (15-channel, TR/TE=2200/27ms) from Fast MRI database21 and 1.5T SSFP cardiac data (28-channel, TR/TE/TI=28.5/1.43/300ms) from OCMR database22. Brain and knee data were compressed to 6-channel by coil compression23,24. All MR data were retrospectively undersampled in a uniform manner while preserving 24, 36, or 24 (out of 218, 320, or 120) central k-space lines for the brain, knee or cardiac data, respectively, as coil calibration data. The proposed method was evaluated and compared to ESPIRiT.
Results
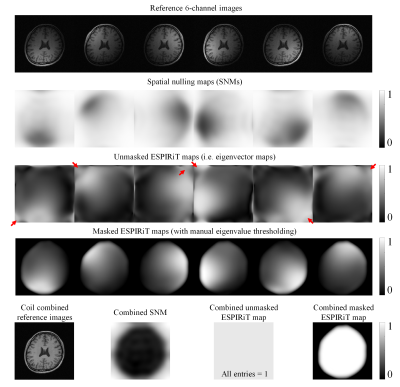
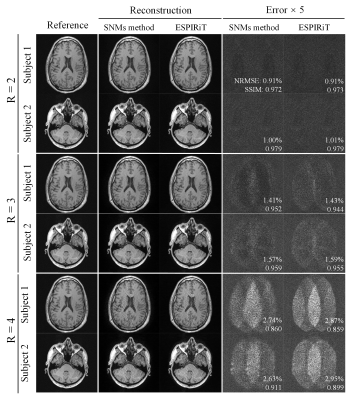
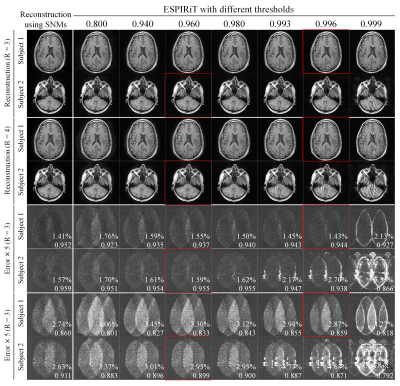
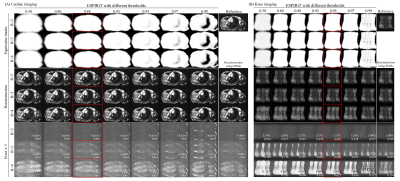
Figure 2 displays a typical set of the SNMs, clearly indicating that, in contrast to ESPIRiT maps, SNMs contain both coil sensitivity and finite image support information. As shown in Figure 3, our proposed method provided reconstruction results with noise level and residual artifacts that were highly comparable to ESPIRiT. Typical reconstruction time was 1-2s per slice for our method. Figure 4 and Figure 5 show the results of our proposed method vs. ESPIRiT reconstruction results that utilized different eigenvalue thresholds for masking coil sensitivity information. They clearly indicate the need for manual thresholding of eigenvector maps before reconstruction in ESPIRiT method, which is eliminated in our proposed method. Our proposed method achieved overall low noise and artifact level compared with ESPIRiT, especially at high acceleration.Discussion and Conclusions
Both our proposed method and ESPIRiT extend the subspace notion of PRUNO and provide computationally more efficient and flexible hybrid-domain reconstruction. However, unlike ESPIRiT, spatial nulling maps in our proposed method contain both coil sensitivity and finite image support information. Our proposed method is also more tolerant of inaccurate subspace separation than ESPIRiT (data not shown) because the number of signal-subspace bases is much smaller than the number of null-subspace bases (i.e., l<n) due to redundancy and linear dependency within MR data. It can also be readily incorporated with regularization for noise reduction.In summary, we have developed a flexible and efficient hybrid-domain reconstruction method, yielding results that are highly comparable to ESPIRiT with optimal manual masking. It eliminates the need for coil sensitivity masking, thus offering a more robust PI reconstruction procedure in practice.
Acknowledgements
This work was supported in part by Hong Kong Research Grant Council (R7003-19F, HKU17112120, HKU17127121 and HKU17127022 to E.X.W., and HKU17103819, HKU17104020 and HKU17127021 to A.T.L.L.), Lam Woo Foundation, and Guangdong Key Technologies for AD Diagnostic and Treatment of Brain (2018B030336001) to E.X.W..References
[1] Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med 1999;42(5):952-962.
[2] Pruessmann KP, Weiger M, Börnert P, Boesiger P. Advances in sensitivity encoding with arbitrary k-space trajectories. Magn Reson Med 2001;46(4):638-651.
[3] Xie VB, Lyu M, Liu Y, Feng Y, Wu EX. Robust EPI Nyquist ghost removal by incorporating phase error correction with sensitivity encoding (PEC-SENSE). Magn Reson Med 2018;79(2):943-951.
[4] Willig-Onwuachi JD, Yeh EN, Grant AK, Ohliger MA, McKenzie CA, Sodickson DK. Phase-constrained parallel MR image reconstruction. J Magn Reson 2005;176(2):187-198.
[5] Weiger M, Pruessmann KP, Boesiger P. 2D SENSE for faster 3D MRI. Magma 2002;14(1):10-19.
[6] Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med 2002;47(6):1202-1210.
[7] Sodickson DK, Griswold MA, Jakob PM. SMASH imaging. Magn Reson Imaging Clin N Am 1999;7(2):237-254, vii-viii.
[8] McKenzie CA, Ohliger MA, Yeh EN, Price MD, Sodickson DK. Coil-by-coil image reconstruction with SMASH. Magn Reson Med 2001;46(3):619-623.
[9] Jakob PM, Griswold MA, Edelman RR, Sodickson DK. AUTO-SMASH: a self-calibrating technique for SMASH imaging. SiMultaneous Acquisition of Spatial Harmonics. Magma 1998;7(1):42-54.
[10] Heidemann RM, Griswold MA, Haase A, Jakob PM. VD-AUTO-SMASH imaging. Magn Reson Med 2001;45(6):1066-1074.
[11] Bydder M, Larkman DJ, Hajnal JV. Generalized SMASH imaging. Magn Reson Med 2002;47(1):160-170.
[12] Liu Y, Lyu M, Barth M, Yi Z, Leong ATL, Chen F, Feng Y, Wu EX. PEC-GRAPPA reconstruction of simultaneous multislice EPI with slice-dependent 2D Nyquist ghost correction. Magn Reson Med 2019;81(3):1924-1934.
[13] Zhang J, Liu C, Moseley ME. Parallel reconstruction using null operations. Magn Reson Med 2011;66(5):1241-1253.
[14] Shin PJ, Larson PEZ, Ohliger MA, Elad M, Pauly JM, Vigneron DB, Lustig M. Calibrationless parallel imaging reconstruction based on structured low-rank matrix completion. Magn Reson Med 2014;72(4):959-970.
[15] Lustig M, Pauly JM. SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space. Magn Reson Med 2010;64(2):457-471.
[16] Yi Z, Liu Y, Zhao Y, Xiao L, Leong ATL, Feng Y, Chen F, Wu EX. Joint calibrationless reconstruction of highly undersampled multicontrast MR datasets using a low-rank Hankel tensor completion framework. Magn Reson Med 2021;85(6):3256-3271.
[17] Liu Y, Yi Z, Zhao Y, Chen F, Feng Y, Guo H, Leong ATL, Wu EX. Calibrationless parallel imaging reconstruction for multislice MR data using low-rank tensor completion. Magn Reson Med 2021;85(2):897-911.
[18] Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, Lustig M. ESPIRiT--an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med 2014;71(3):990-1001.
[19] Hestenes MR, Stiefel E. Methods of Conjugate Gradients for Solving Linear Systems. J Res Natl Bureau Stand 1952;49(6):409-436.
[20] Souza R, Lucena O, Garrafa J, Gobbi D, Saluzzi M, Appenzeller S, Rittner L, Frayne R, Lotufo R. An open, multi-vendor, multi-field-strength brain MR dataset and analysis of publicly available skull stripping methods agreement. NeuroImage 2018;170:482-494.
[21] Knoll F, Zbontar J, Sriram A, Muckley MJ, Bruno M, Defazio A, Parente M, Geras KJ, Katsnelson J, Chandarana H, Zhang Z, Drozdzalv M, Romero A, Rabbat M, Vincent P, Pinkerton J, Wang D, Yakubova N, Owens E, Zitnick CL, Recht MP, Sodickson DK, Lui YW. fastMRI: a publicly available raw k- space and DICOM dataset of knee images for accelerated MR image reconstruction using machine learning. Radiol Artif Intell 2020;2(1):e190007.
[22] Chen C, Liu Y, Schniter P, Tong M, Zareba K, Simonetti O, Potter L, Ahmad R. OCMR (v1.0)--Open-Access Dataset for Multi-Coil k-Space Data for Cardiovascular Magnetic Resonance Imaging2020
[23] Buehrer M, Pruessmann KP, Boesiger P, Kozerke S. Array compression for MRI with large coil arrays. Magn Reson Med 2007;57(6):1131-1139.
[24] Zhang T, Pauly JM, Vasanawala SS, Lustig M. Coil compression for accelerated imaging with Cartesian sampling. Magn Reson Med 2013;69(2):571-582.
Figures