Synopsis

Keywords: Sparse & Low-Rank Models, Quantitative Imaging

Subspace or low-rank models have been demonstrated useful in producing efficient representations and reconstructions for high dimensional imaging problems. In this study, we propose an unsupervised learning-based approach by generalizing the subspace model using a deep generative network. The generative subspace model can then be incorporated into the physics-based reconstruction formalism. The network parameters can be self-trained by minimizing the cost function with the flexibility to integrate with conventional constraints. We demonstrated the effectiveness of the proposed method over standard linear subspace and deep image prior models using in vivo T2 mapping dataset.

Introduction

High-dimensional MR imaging, such as parameter mapping, dynamic imaging and spectroscopic imaging, have shown considerable potential in many clinical and basic science applications. However, the long scan times caused by the high dimensionality hinders practical applications. Subspace or low-rank models¹ have become a widely used tool to address the dimensionality challenge by exploiting the intrinsic redundancy in high-dimensional image functions of interest^2-4. In the meantime, deep learning (DL)-based methods have shown significant potential for accelerating high-dimensional imaging by improving image reconstruction from sparsely sampled data. Most DL methods exploited cascaded or unrolled network structures^5,6 to learn an end-to-end mapping from the undersampled data/image to the desired image functions. These supervised approaches rely on the large quantities of high-quality training datasets to learn data-adaptive image priors, which are often challenging to collect for high-dimensional imaging problems. Self-supervised learning approaches^7,8 have also been developed for dynamic imaging and parameter mapping and shown promising results. In this study, we proposed an unsupervised learning-based method that generalizes the linear subspace model using a deep generative network. The network-based representation was then incorporated into the imaging equation for reconstruction. In vivo T2 mapping dataset was used to demonstrate the superior performance of our method over the standard subspace and deep image prior methods.

Theory and Methods

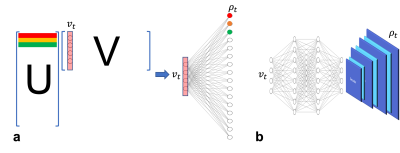
According to the partial separability theory¹, a spatiotemporal function $$$\rho(r,t)$$$ in MRI can usually be approximately by a linear subspace model, whose matrix form can be expressed as:$$\rho=UV$$ where $$$U\in\mathbb{C}^{N\times L}$$$ and $$$V\in\mathbb{C}^{L\times T}$$$ are the spatial coefficients and temporal basis, respectively. $$$L$$$ is the model order or the rank. At each time point $$$t$$$, the image function $$$\rho_t$$$ can be written as:$$\rho_t=Uv_t$$ where $$$v_t\in\mathbb{C}^{L\times 1}$$$ denotes the column vector of $$$V$$$ at time point $$$t$$$. In other words, each voxel in $$$\rho_t$$$ can be considered as a linear combination of elements in $$$v_t$$$ with different weights (i.e., row vectors) stored in $$$U$$$. In addition, voxels from different time points share the same weights in $$$U$$$. This linear representation is equivalent to one fully connected layer with linear activation function as illustrated in Fig. 1. Motivated by this reformulation, we propose the following generative subspace model to create a feature-based representation of the “time-independent” spatial variations with the same temporal basis:$$\rho_t=\mho(v_t,\theta)$$ where $$$\mho$$$ is a generative model defined by a deep neural network with trainable parameter $$$\theta$$$. To this end, the generative model can be incorporated into the forward physical imaging equation with conventional regularizations:$$\underset{\theta}{\operatorname{argmin}} \sum_{t}^{}\left\| d_t-F_uS\mho(v_t,\theta)\right\|^2_2 + \lambda R(\sum_{t}\mho(v_t,\theta))$$ where $$$d_t$$$ denotes the undersampled k-space data at time point $$$t$$$, $$$F_u$$$ is the undersampled Fourier operator, $$$S$$$ is the coil sensitivity function, $$$R(\cdot)$$$ can be selected to enforce joint sparsity of the temporal images in certain transform domain. The network structure governing the generative model is illustrated in Fig. 1b. Inspired by the linear subspace model, we replace the linear weights with a three-layer perceptron, mapping $$$v_t$$$ to a latent space with dimension $$$m<<N$$$. Afterwards, a convolutional decoder is designed to restore the full resolution image from its latent space features. The key assumption is that the column vectors in $$$V$$$ contain sufficient information to infer the corresponding spatial images given the flexible and powerful representation capability of the nonlinear models. The network parameters can be directly estimated by minimizing the above cost function using stochastic gradient descent with an Adam optimizer over all the time points repeatedly until convergence in a self-supervised fashion.

Experiments and Results

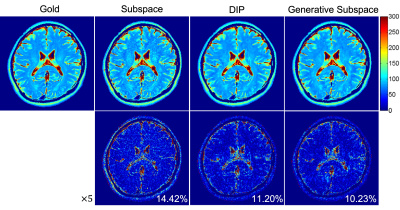
We evaluated the proposed method using in vivo T2 mapping datasets acquired on a 3T scanner using turbo spin echo sequence with a 12-channel head coil array (resolution 1×1mm², slice thickness=3.0mm, ETL=16, TE1=ΔTE=8.8ms, TR=4000ms). The network was constructed in pyTorch and self-trained using one NVIDIA RTX A6000 GPU for 30 thousand iterations. The temporal basis was computed using singular value decomposition (SVD) from 5 central k-space lines across all echoes. The coil sensitivity functions were estimated from the center k-space of the 1st echo (i.e., 42 lines, R=6) using ESPIRiT⁹. Conventional subspace model and deep image prior¹⁰ methods were implemented for comparison.
The reconstructed T2 maps are compared in Fig. 2. As can be seen, the generative subspace model outperforms the linear subspace model owing to the increased representation capability and the intrinsic spatial priors imposed by the network structure. Our method also exceeds the state-of-the-art deep image prior method (i.e., taking random variables as network input), demonstrating essential information captured by the basis functions.

Conclusion

We developed an unsupervised approach for high dimensional MRI using a generative subspace model. Future work will study the integration of the generative subspace model with conventional constraints (e.g., sparsity) and validate the proposed method for other MRI problems including dynamic imaging and spectroscopic imaging.

Acknowledgements

No acknowledgement found.