0856
Compressed sense reconstructions improve non-Cartesian hyperpolarized 129Xe MRI
Joseph W Plummer1,2, Abdullah S Bdaiwi1,2, Stephanie A Soderlund1, Matthew M Willmering1, Jason C Woods1,3,4,5, Zackary I Cleveland1,2,4,5, and Laura L Walkup1,2,4,5
1Center for Pulmonary Imaging Research, Department of Pulmonary Medicine, Cincinnati Children's Hospital Medical Center, Cincinnati, OH, United States, 2Department of Biomedical Engineering, University of Cincinnati, Cincinnati, OH, United States, 3Department of Physics, University of Cincinnati, Cincinnati, OH, United States, 4Department of Radiology, Cincinnati Children's Hospital Medical Center, Cincinnati, OH, United States, 5Department of Pediatrics, Cincinnati Children's Hospital Medical Center, Cincinnati, OH, United States
1Center for Pulmonary Imaging Research, Department of Pulmonary Medicine, Cincinnati Children's Hospital Medical Center, Cincinnati, OH, United States, 2Department of Biomedical Engineering, University of Cincinnati, Cincinnati, OH, United States, 3Department of Physics, University of Cincinnati, Cincinnati, OH, United States, 4Department of Radiology, Cincinnati Children's Hospital Medical Center, Cincinnati, OH, United States, 5Department of Pediatrics, Cincinnati Children's Hospital Medical Center, Cincinnati, OH, United States
Synopsis
Keywords: Hyperpolarized MR (Gas), Image Reconstruction
Hyperpolarized 129Xe MRI is a powerful pulmonary imaging modality to assess regional ventilation, gas exchange, and lung microstructure. However, non-equilibrium magnetization decay and relatively long breath-hold durations remain major limitations to routine clinical dissemination. While non-Cartesian sampling methods can improve sampling efficiency, these methods are yet to be combined with non-linear reconstruction methods like compressed sensing to further increase speed and reduce image noise. Here, we implement compressed-sense reconstructions across a range of non-Cartesian 129Xe MRI techniques and show that SNR and image quality can all be improved while reducing scan time.Introduction
Hyperpolarized Xe MRI is a powerful pulmonary imaging modality used to assess gas distribution (ventilation1), airspace dynamics (diffusion-weighted2), and gas-transfer to the red-blood cells (gas-exchange3). Typically, Xe MRI scans are performed within a ≤16-second breath-hold, limiting the attainable SNR, resolution, and dynamic information. Non-Cartesian methods, including 2D-spiral and 3D-FLORET, have improved sampling efficiency4; however, they are yet to be combined with non-linear reconstruction methods like compressed sensing (CS). Here, we demonstrate CS reconstructions across a range of non-Cartesian Xe MRI techniques, and show that SNR, imaging speed, and image quality are improved.Theory
Non-Cartesian measurements can be reconstructed into an image, $$$x$$$, by solving the following forward model problem:$$b = Ax + ε, \tag{1}$$
where $$$b$$$ is the k-space data; $$$A$$$ is the measurement matrix; and $$$ε$$$ is the additive noise. (1) is solved by matrix inversion of $$$A=DF$$$ with $$$b$$$, where $$$D$$$ is the density compensation used to precondition $$$A$$$, and $$$F$$$ is the non-uniform fast Fourier transform5 (NUFFT). However, the inverse model approach ($$$A^{-1}$$$) is not robust to under-sampled measurements or ill-conditioned $$$A$$$—as is often the case for non-Cartesian sampling—leading to noisy reconstructions.
Alternately, (1) can be solved using iterative optimization methods by recasting to a regularized least squares problem, like an iterative NUFFT6. Such methods enable the use of regularizers to converge on solutions that have minimal energy in some transformed domain. A common example is the multi-regularizer CS problem7:
$$x^\star=\underset{x}{\min}\frac{1}{2}|| Ax -b ||_2 + \lambda_1 ||W(x)||_1 + \lambda_2||G(x)||_2, \tag{2}$$
where the reconstructed image, $$$x^\star$$$, is regularized ($$$\lambda_i$$$) for both wavelet-transform energy ($$$W(x)$$$; efficient for preserving edges/low contrast information) and total variation ($$$G(x)$$$; efficient at suppressing noise/streaking). To date, such methods have yet to be rigorously investigated in non-Cartesian Xe MRI. Here, we compare reconstructions using $$$A^{-1}$$$ versus CS in ventilation, diffusion-weighted, and gas-exchange imaging.
Methods
Seventeen healthy subjects (21-65 y.o.; 10M/7F) were imaged after obtaining informed consent per a protocol approved by our local Institutional Review Board (2014-5279 with FDA IND-123,577). 86%-enriched 129Xe was polarized to 30-40% using a continuous-flow hyperpolarizer (Polarean 9820A, Durham, NC)8. Images were collected on a Philips 3T-Ingenia scanner with a custom chest coil (Clinical MR solutions, Brookfield, WI). Simulated point-spread functions/ventilation sequences included: 2D-radial, 2D-spiral, 3D-radial, and 3D-FLORET4; diffusion-weighted: 2D-spiral2; gas-exchange: 3D-radial9. Technical parameters are included in figure captions.$$$A^{-1}$$$ images were reconstructed via density-compensated inverse NUFFT5,10. CS images were reconstructed using the alternating direction method of multipliers algorithm11 in SigPy12. $$$\lambda_1$$$ and $$$\lambda_2$$$ ranged from 1x10-5 to 1x10-3. Statistical differences were assessed with Wilcoxon signed-rank tests.
Results
Figure 1 contains simulated point-spread functions to examine noise incoherence using 100% and 50% of projections for 2D-radial/spiral and 3D-radial/FLORET acquisitions. The same settings are demonstrated in ventilation imaging (Figure 2). In all cases, CS increased SNR/image quality, even with 50% sub-sampling.$$$A^{-1}$$$ and CS reconstructions are shown for diffusion-weighted imaging (single subject: Figure 3A/B; all subjects: Figure 3C/D). CS significantly increased SNR across all b-values (P<0.01), preserved the mean apparent diffusion coefficient (ADC) (P=0.63), and decreased ADC variation (P<0.01).
Gas-exchange reconstructions are shown in Figure 4A/B. CS reduced streaking artifacts, increased SNR, and preserved phase. Additionally, CS preserved the median signal intensity, μ, and reduced variation, σ, and skewness, ν (Figure 4C/D).
Finally, 50% sub-sampled gas-exchange reconstructions were performed with CS in a healthy cohort (Figure 5). Mean SNR increased significantly (P<0.01) using CS in 100% and 50% sampling relative to $$$A^{-1}$$$. μ was preserved, while σ decreased (dissolved) and ν increased (gas/dissolved) significantly (P<0.05).
Discussion
CS most benefits under-sampled acquisitions that produce incoherent noise/aliasing. Point-spread functions for sub-sampled radial projections demonstrate this, as 50% and 100% sub-sampled reconstructions varied only by an incoherent noise floor (Figure 1A/B). Point-spread functions for sub-sampled spirals showed similar patterns inside the field-of-view, with coherent aliasing only appearing on the edges (Figure 1C/D). Consequently, when applied to ventilation (Figure 2), CS suppressed noise and increased SNR for all sequences. Notably, improvements in 3D-radial/FLORET (even with 50% sub-sampling) suggest that significant reductions to scan duration are possible (i.e., decreasing required breath-hold from 16- to 8-seconds).CS also improved diffusion-weighted imaging, increasing SNR for each b-value image by >50% (Figure 3C), thereby reducing ADC measurement uncertainty13 (Figure 3D). Consequently, CS reduced the variation in ADC, while preserving the mean.
Gas-exchange MRI is prospectively under-sampled to fit within a 16-second breath-hold (~19%-Nyquist) and suffers from low Xe solubility in pulmonary tissues (<14%)14, ultimately limiting gas/dissolved-phase signal. However, in Figures 4/5, CS increased SNR ~two-fold in both gas and dissolved-phases. Across the healthy cohort, CS preserved μ while decreasing σ, consistent with noise suppression. CS increased ν, consistent with underlying bias-field effects or gravitational-induced physiology (especially in the dissolved-phase) being uncovered. Gas-exchange images exhibited largely incoherent noise when using 50%-total projections, which CS effectively suppresses. The mean SNR increased for 50% sub-sampled CS compared to 100% sampled $$$A^{-1}$$$ reconstructions, while μ/σ were preserved/reduced (Figure 5C-F). Practically, a CS-reconstructed, 50% sub-sampled 3D-radial gas-exchange sequence reduces a breath-hold by two-fold, becoming more feasible for young children and advanced lung disease patients.
Conclusion
This work demonstrates that combining non-Cartesian sampling with CS reconstruction improves SNR/image quality while reducing scan duration in Xe ventilation, diffusion-weighted, and gas-exchange MRI.Acknowledgements
The authors would also like to thank hyperpolarized gas research assistant: Carter McMaster; MRI technologists: Kaley Bridgewater, Kelsey Murphy, Sarah Miozzi, and Matthew Lanier; clinical research coordinators: Priyanka Desirazu, Megan Schmitt, and Alex Rizkallah; and the research nurses at Cincinnati Children’s Hospital.References
- Mugler, J.P. and T.A. Altes, Hyperpolarized 129Xe MRI of the human lung. J Magn Reson Imaging, 2013. 37(2): p. 313-31.
- Bdaiwi, A.S., et al., Diffusion weighted hyperpolarized 129Xe MRI of the lung with 2D and 3D (FLORET) spiral. Magn Reson Med, 2022.
- Kaushik, S.S., et al., Single-breath clinical imaging of hyperpolarized 129xe in the airspaces, barrier, and red blood cells using an interleaved 3D radial 1-point Dixon acquisition. Magnetic Resonance in Medicine, 2016. 75(4): p. 1434-1443.
- Willmering, M.M., et al., Improved pulmonary 129Xe ventilation imaging via 3D-spiral UTE MRI. Magnetic Resonance in Medicine, 2020. 84(1): p. 312-320.
- Fessler, J.A., On NUFFT-based gridding for non-Cartesian MRI. J Magn Reson, 2007. 188(2): p. 191-5.
- Fessler, J.A. and B.P. Sutton, Nonuniform fast Fourier transforms using min-max interpolation. IEEE Transactions on Signal Processing, 2003. 51(2): p. 560-574.
- Lustig, M., D. Donoho, and J.M. Pauly, Sparse MRI: The application of compressed sensing for rapid MR imaging. Magnetic Resonance in Medicine, 2007. 58(6): p. 1182-1195.
- Plummer, J.W., et al., A semi-empirical model to optimize continuous-flow hyperpolarized 129Xe production under practical cryogenic-accumulation conditions. Journal of Magnetic Resonance, 2020. 320: p. 106845.
- Niedbalski, P.J., et al., Protocols for multi-site trials using hyperpolarized 129Xe MRI for imaging of ventilation, alveolar-airspace size, and gas exchange: A position paper from the 129Xe MRI clinical trials consortium. Magnetic Resonance in Medicine, 2021. 86(6): p. 2966-2986.
- Pipe, J.G. and P. Menon, Sampling density compensation in MRI: rationale and an iterative numerical solution. Magn Reson Med, 1999. 41(1): p. 179-86.
- Parikh, N. and S. Boyd, Proximal Algorithms. Foundations and Trends® in Optimization, 2014. 1(3): p. 127-239.
- Ong, F. and M. Lustig. SigPy: a python package for high performance iterative reconstruction. in Proceedings of the ISMRM 27th Annual Meeting, Montreal, Quebec, Canada. 2019.
- Bdaiwi, A.S., et al., Improving hyperpolarized (129) Xe ADC mapping in pediatric and adult lungs with uncertainty propagation. NMR Biomed, 2021: p. e4639.
- Cleveland, Z.I., et al., Hyperpolarized Xe MR imaging of alveolar gas uptake in humans. PloS one, 2010. 5(8): p. e12192-e12192.
Figures
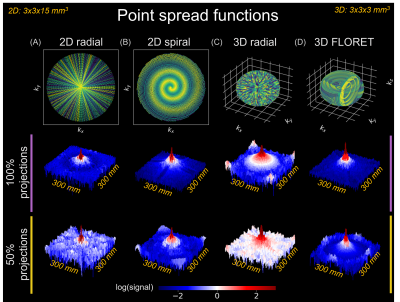
Point spread functions (log-scaled) following
inverse model approach ($$$A^{-1}$$$) reconstructions of (A) 2D-radial
(projections=246, TR/TE=4.25/0.85 ms); (B) 2D-spiral (variable-density,
interleaves=24, TR/TE=10.1/1.53 ms); (C) 3D-radial (projections=3670,
TR/TE=4.00/0.04 ms); and (D) 3D-FLORET (interleaves=1134,
TR/TE=13.1/0.08 ms) sequences. Matrix size=100, resolution=3x3x15 mm3
(2D), 3x3x3 mm3 (3D), FOV=300 mm3. Reconstructions
performed with 100% and 50% projections of Nyquist limit.
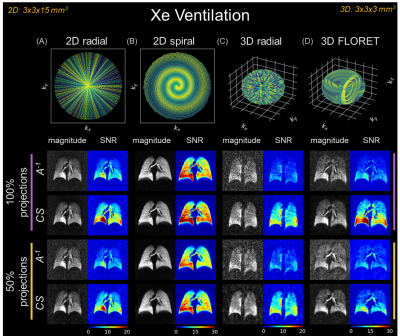
Ventilation images following inverse
model ($$$A^{-1}$$$) and compressed sense (CS) reconstructions
of (A) 2D-radial (projections=246, TR/TE=4.25/0.85 ms); (B)
2D-spiral (variable-density, interleaves=24, TR/TE=10.1/1.53 ms); (C) 3D-radial
(projections=3670, TR/TE=4.00/0.04 ms); and (D) 3D-FLORET
(interleaves=1134, TR/TE=13.1/0.08 ms). Matrix size=100, resolution=3x3x15 mm3
(2D), 3x3x3 mm3 (3D), FOV=300 mm3, flip-angle=2-13⁰.
Reconstructions performed with 100% and 50% projections of Nyquist limit.
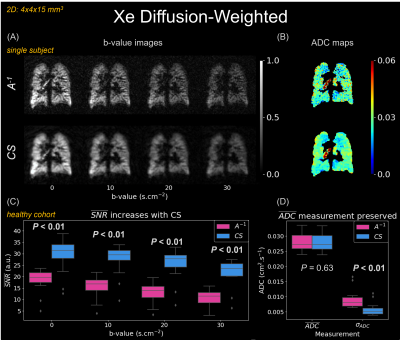
(A) Diffusion-weighted
images (2D-spiral, uniform-density, matrix size=100, resolution=4x4x15 mm3,
TR/TE=81.3/12.9 ms, flip-angle=6-10⁰). (B) Apparent diffusion
coefficient (ADC) maps calculated from (A)2, 9. ADC with
CS becomes more uniform while maintaining similar magnitude. (C) Box
plots comparing mean SNR of $$$A^{-1}$$$ and
CS images (Wilcoxon signed-rank test). CS significantly improves SNR across all
b-values. (D) CS maintains the mean lung ADC, $$$\overline{ADC}$$$, while decreasing the standard
deviation, σADC.
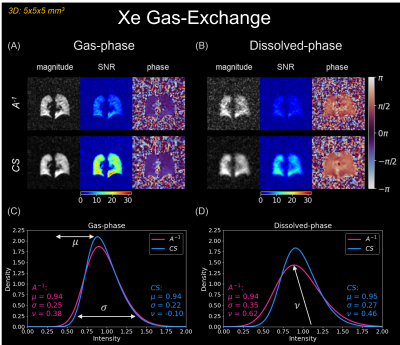
CS reconstructions in 3D-radial
gas-exchange imaging (matrix size=64, projections=2400, resolution=5x5x5 mm3,
TR/TE=4.0/~0.47 ms, flip-angle=~0.5⁰ (gas)/15⁰ (dissolved))9. $$$A^{-1}$$$ and CS reconstructed images, SNR, and phase
maps for (A) gas-phase, and (B) dissolved-phase. SNR
increases with CS, while phase is preserved. (C) and (D) compared
distribution parameters: median signal intensity, μ, coefficient of variation, σ, and coefficient of skewness, ν, between methods.
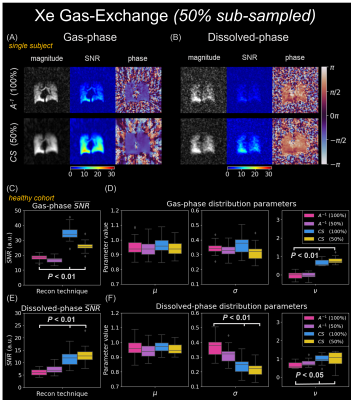
CS reconstructions in 50% sub-sampled (of
all 2400 projections, Figure 4) 3D-radial gas-exchange imaging. $$$A^{-1}$$$ (100%
sampled) and CS (50% sampled) reconstructed images, SNR, and phase maps for (A)
gas-phase, and (B) dissolved-phase. (C) and (D) show
boxplots to compare SNR and distribution parameters between methods (Wilcoxon
signed-rank test). SNR increases significantly, while μ is preserved (both); σ is
preserved (gas) and decreases (dissolved); and ν increases
(both).
DOI: https://doi.org/10.58530/2023/0856