Synopsis

Keywords: Parallel Imaging, Machine Learning/Artificial Intelligence, Noise-robust method

We propose a novel loss function that increases noise-robustness in accelerated parallel MR image reconstruction. The loss function is based on the variance of the background area in the noisy undersampled image and that of the difference image between noisy undersampled image and the synthesized undersampled image. The proposed loss function provides stronger regularization and robustness when applied along with other constraints. We show that the application of the proposed loss function boosts performance of the network, yielding improved quality of reconstructed image.

Introduction

Accelerated magnetic resonance imaging (MRI), which shortens scan time by acquiring undersampled k-space data, is one of the most promising methods for scan time reduction. In the past few years, deep learning-based approaches^1-4 have successfully achieved improved quality of reconstructed images with higher acceleration factor compared to the conventional methods such as compressed sensing (CS). However, the performance degrades significantly with higher noise level, especially for accelerated MRI reconstruction with sparse sampling. With noisy data, not only may the CS method not converge to the best solution⁵, but also deep learning-based methods may fail to reconstruct an accurate image⁶. To deal with these issues, we propose a novel noise-robust loss function that can be applied to deep learning-based accelerated MRI reconstruction frameworks. Our results indicate that the proposed loss function successfully boosts performance of reconstructing full-sampled image from noisy undersampled input.

Method

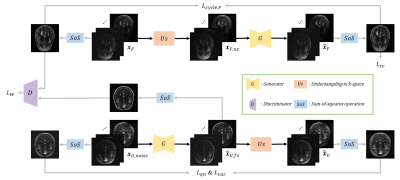
In this work, optimal transport driven CycleGAN (OT-cycleGAN)³ is used as the accelerated MRI reconstruction framework, as illustrated in Fig. 1. Originally, OT-cycleGAN utilizes L1 cycle loss in the undersampled branch, but the generator is not properly trained with noisy input data. Therefore, we replace the L1 cycle loss with quasi norm-based (QN) loss⁷, which models the residuals between two images as generalized Gaussian distribution. $$\mathcal{L}_{qn}=-\sum\limits_{i=1, j=1}^{i=T, j=K}-\left(\frac{\left|\mathcal{F}^{-1}\mathcal{P}\mathcal{F}\left[G\left(x_{U,noise}\right)_{ij}-\left(x_{U,noise}\right)_{ij}\right]\right|}{\alpha_{ij}}\right)^{\beta_{ij}}+\log{\left(\frac{\beta_{ij}}{2\alpha_{ij}}\right)}-\log{\Gamma\left(\frac{1}{\beta_{ij}}\right)},$$ where $$$\mathcal{F}$$$, $$$\mathcal{F}^{-1}$$$, and $$$\mathcal{P}$$$ represent the Fourier transform, the inverse Fourier transform, and the undersampling operation, respectively. Furthermore, $$$G$$$ is the generator, $$$x_{U,noise}$$$ is the noisy undersampled input, $$$\Gamma$$$ is the standard gamma function, and $$$\alpha_{ij}$$$ and $$$\beta_{ij}$$$ are the scale and shape parameters on each pixel location, respectively.
Total variation (TV) loss is a widely accepted noise-robust loss function, which minimizes the difference between neighboring pixels. TV loss is applied to the difference image between the input full-sampled image and the generated full-sampled image to give a smoothing effect on the reconstructed image.$$\mathcal{L}_{tv}=\mathbb{E}\left[\lVert{x_{F}-G\left(\mathcal{F}_{-1}\mathcal{P}\mathcal{F}x_{F}\right)}\rVert_{tv}\right],$$ where $$$x_{F}$$$ represents the full-sampled input image and $$$\lVert{\cdot}\rVert_{tv}$$$ represents the difference between neighboring pixels for each pixel.
The proposed loss function in this work is the variance loss. Generally, MR images contain the foreground area with signals of the interested body part and the background area without the signal. Therefore, the background of the MR image contains noise information. Meanwhile, if the generator produces a full-sampled output image, the difference image between the generated undersampled image and the noisy undersampled image should only contain the noise components. We define a loss between the variance of the background area in the noisy undersampled input and the variance of the difference image.$$\mathcal{L}_{var}=\lVert{Var\left(x_{U,noise,bg}\right)-Var\left(\hat{x}_{U}\right)}\rVert,$$ where $$$Var\left(\cdot\right)$$$ represents the noise variance value, $$$x_{U,noise,bg}$$$ represents the background area of noisy undersampled input, and $$$\hat{x}_{U}$$$ represents the generated undersampled image.
The total generator loss function is as follows with Wasserstein loss $$$\left(\mathcal{L}_{W}\right)$$$ and L1 cycle loss of the full sampled branch $$$\left(\mathcal{L}_{cycle}\right)$$$:$$\mathcal{G}=\mathcal{L}_{W}+\lambda_{cycle}\mathcal{L}_{cycle}+\lambda_{qn}\mathcal{L}_{qn}+\lambda_{tv}\mathcal{L}_{tv}+\lambda_{var}\mathcal{L}_{var}.$$
The total discriminator loss function is as follows with Wasserstein loss $$$\left(\mathcal{L}_{W,D}\right)$$$ and gradient penalty loss $$$\mathcal{L}_{gp}$$$:$$\mathcal{L}_{D}=\mathcal{L}_{W,D}+\lambda_{gp}\mathcal{L}_{gp}.$$
We used the brain MR data acquired with 20-channel coil in the FastMRI dataset. We extracted 600 slices from 100 MR data for training set and 36 slices from 6 MR data for test set. For undersampling, 1D Cartesian non-uniform sampling mask was used with 16 ACS lines and an acceleration factor of 4. Random complex Gaussian noise was added to each coil data with sigma values ranging from 0 to 0.03 when the maximum signal intensity was 1 in image domain.
In our implementation, both the generator and the discriminator were trained with Adam optimizer, momentum parameters set to $$$\beta_{1}=0.5$$$ and $$$\beta_{2}=0.9$$$. We used residual U-net for the generator network, and was updated once per 5 updates of the discriminator. The batch size was 1, the learning rate was set to 0.0005, and trained for 100 epochs. For the loss weights, $$$\lambda_{gp}=10$$$, $$$\lambda_{cycle}=100$$$, $$$\lambda_{qn}=5e^{-9}$$$, $$$\lambda_{tv}=200$$$, and $$$\lambda_{var}=1$$$.

Results

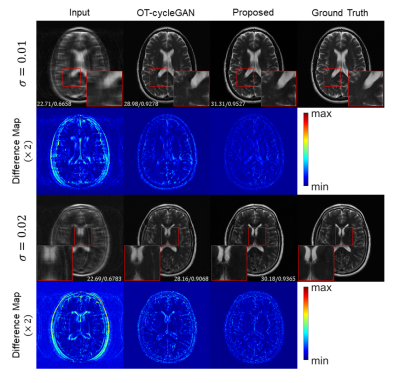
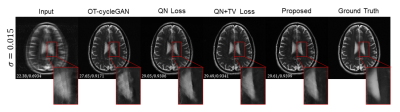
The proposed method significantly improved the reconstructed image quality compared to the OT-cycleGAN, where the reconstructed images are shown in Fig. 2. With higher noise level, OT-cycleGAN generated noisy output with unresolved aliasing artifacts. In contrast, the proposed method successfully generated smooth image without any artifacts.
To show that the applied loss functions improved the output image quality, ablation study was conducted. The results are depicted in Fig. 3, where improvements can be seen with each loss function applied. Furthermore, quantitative results are shown in Table 1. The proposed method achieved the best PSNR and SSIM scores not only when tested with various noise levels, but also when tested with constant noise levels. This indicates that the proposed method is undoubtedly effective for accelerated MR image reconstruction of undersampled input data corrupted with various ranges of noise.

Discussion and Conclusion

In this work, we proposed a novel loss function for more noise-robust accelerated MRI reconstruction framework. We showed that the application of variance loss successfully improved reconstruction performance. Despite the fact that the noise distributions in the foreground and background areas become different after root-sum-of-square operation, the variance loss works as a meaningful regularization along with QN loss and TV loss. The proposed loss can be implemented in other accelerated MRI reconstruction frameworks based on unsupervised or self-supervised learning methods, providing stronger constraint for both reconstruction and denoising.

Acknowledgements

This research was supported by a grant of the Korea Health Technology R&D Project through the Korea Health Industry Development Institute (funded by the Ministry of Health Welfare, Republic of Korea grant number HI 14 C 1135)