0830

Using Noisier2Noise to choose the sampling mask partition of Self-Supervised Learning via Data Undersampling (SSDU)

Charles Millard¹ and Mark Chiew¹
¹Wellcome Centre for Integrative Neuroimaging, FMRIB, University of Oxford, Oxford, United Kingdom

Synopsis

Keywords: Image Reconstruction, Machine Learning/Artificial Intelligence, Self-supervised learning

To train a neural network to recover images with sub-sampled examples only, Self-Supervised Learning via Data Undersampling (SSDU) proposes partitioning the sampling mask into two subsets and training a network to recover one from the other. Recent work on the connection between SSDU and the self-supervised denoising method Noisier2Noise has shown that superior reconstruction quality is possible when the distribution of the partition matches the sampling mask. We test this principle on three types of sampling schemes and find that the test set loss is indeed closest to a fully supervised benchmark when the partition distribution is matched.

Introduction

The majority of existing methods for MRI reconstruction with deep learning are fully supervised, so require a fully sampled dataset for training. However, in many cases, such a dataset is not available and may be difficult to acquire in practice.

More recently, there has been interest in methods that train neural networks to reconstruct sub-sampled MRI data in a self-supervised manner, where the training data is itself sub-sampled^1-4. One approach that has been shown to perform competitively with fully supervised training is Self-Supervised Learning via Data Undersampling (SSDU)⁴, which proposes randomly partitioning the sampling set into two sets and training a network to map from one subset to the other. Here, we use recent developments by the present authors on the connection between SSDU and the self-supervised denoising method Noisier2Noise^5,6 to inform the distribution of the sampling set partition.

Theory

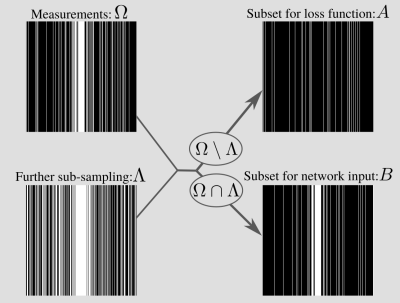
Denote the training data as $$$y_{t}=M_{\Omega_t}y_{0,t}$$$, where $$$M_{\Omega_t}$$$ is a mask with sampling set $$$\Omega_t$$$, $$$y_{0,t}$$$ is fully sampled k-space, and $$$t$$$ indexes the training set. To train a network to reconstruct images with sub-sampled examples only, SSDU⁴ proposes partitioning $$$\Omega_t$$$ into two disjoint sets $$$A_t$$$ and $$$B_t$$$, so that $$$A_t\cup B_t=\Omega_t$$$ and $$$A_t\cap B_t=\emptyset$$$. Then, a network $$$f_\theta$$$ with parameters $$$\theta$$$ is trained by minimizing the loss $$ \sum_t L(M_{A_t}f_\theta(M_{B_t} y_t), M_{A_t} y_t)$$ for some function $$$L$$$. At inference the estimate uses all available data.

The present authors have recently shown that SSDU is closely connected to the self-supervised denoising method Noisier2Noise^5,6. The connection has two main consequences: firstly, the mathematical framework of Noisier2Noise can be used to prove SSDU’s empirically observed performance; secondly, it motivates the optimal distribution of the sampling set partition. In this work, we focus on the latter. In particular, Noisier2Noise implies that the distribution of $$$B_t$$$ should match that of $$$\Omega_t$$$, but with different parameters. For instance, if $$$\Omega_t$$$ is (variable density) Bernoulli, an appropriate $$$B_t = \Omega_t \cap \Lambda_t$$$ is one that is also Bernoulli with a different variable density distribution. One way to do this is to generate another, independent set $$$\Lambda_t$$$ and let $$$A_t = \Omega_t\setminus\Lambda_t$$$ and $$$B_t = \Omega_t \cap \Lambda_t$$$⁶. Then $$$B_t$$$ is Bernoulli when $$$\Lambda_t$$$ is Bernoulli. Matching $$$\Lambda_t$$$ to $$$\Omega_t$$$ also holds for other distributions, such as when $$$\Omega_t$$$ consists of independently sampled columns: see Fig. 1.

Intuitively, when $$$B_t$$$ matches $$$\Omega_t$$$, the network cannot distinguish between their contributions to the aliasing, so the loss is minimized when the aliasing due to both is removed. If they are mismatched, a network could in principle remove the aliasing due to $$$B_t$$$ but not $$$\Omega_t$$$, so minimizing SSDU's loss does not necessarily successfully recover the alias-free image.

Method

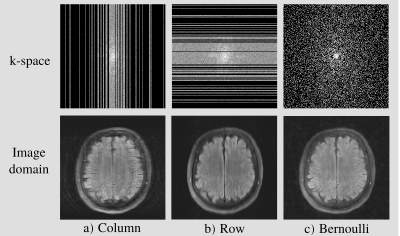
We considered three types of sampling distributions: 1D row sampling, 1D column sampling and 2D Bernoulli sampling, each with polynomial variable density sampling: see in Fig. 2. We trained a network to reconstruct images for all possible combinations of $$$\Omega_t$$$ and $$$\Lambda_t$$$ distributions. For $$$\Omega_t$$$ we used sub-sampling factors 4 and 8. The sub-sampling factor of $$$\Lambda_t$$$ needs to give a $$$B_t$$$ that is small, so that most of k-space remains in the network input, but not empty, so that the loss function is non-zero. We used sub-sampling factor 2, which has previously been found to perform well for column sampling with the same variable density distribution⁶. A new $$$\Lambda_t$$$ was re-generated once per epoch. As a best-case benchmark, we also compared with fully supervised training.

We used the multi-coil fastMRI brain data⁷ and the Variational Network (VarNet) architecture^8,9 with 5 cascades. We used the Adam optimizer with a learning rate of $$$10^{-3}$$$, an $$$\ell_2$$$ loss, and trained for 50 epochs. Our implementation is available at github.com/charlesmillard/Noisier2Noise_for_recon

Results and Discussion

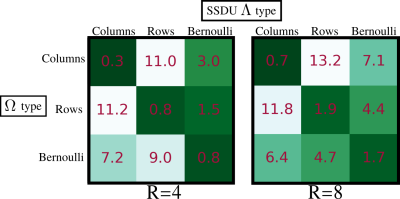
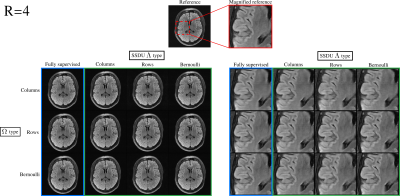
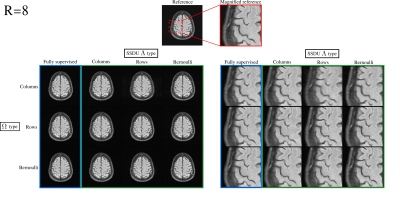
Fig. 3 demonstrates that the test set loss of SSDU is closest to the fully supervised benchmark when $$$\Lambda_t$$$ is matched to $$$\Omega_t$$$. The examples at $$$R=4$$$ and $$$R=8$$$, shown in figures 4 and 5 respectively, illustrate that the qualitative improvement is substantial when $$$\Lambda_t$$$ is matched to $$$\Omega_t$$$, especially at $$$R=8$$$. When $$$\Omega_t$$$ is 1D, the next-best performance is when $$$\Lambda_t$$$ is Bernoulli. When a mixture of rows and columns are used, SSDU performs especially poorly, with streaks caused by $$$\Omega$$$ still visible.

Conclusions

It is widely known that higher quality image restoration is possible when k-space is sub-sampled in both dimensions¹⁰. This work demonstrates that the same principle does not apply in general to SSDU's partitioning set. Rather, SSDU’s performance improves when $$$B_t$$$ has the same distribution as $$$\Omega_t$$$, which may be 1D or 2D. A similar improvement for radial sampling has also previously been empirically observed¹¹.

It is not always possible to choose a partition so that $$$B_t$$$ and $$$\Omega_t$$$ have matching distributions. For instance, the original SSDU paper⁴ considered an $$$\Omega_t$$$ comprised of equidistant columns, which cannot be partitioned in the way suggested in this abstract. Nonetheless, as in this work, it was found that partitioning with a variable density Bernoulli $$$\Lambda_t$$$ performed reasonably well in practice despite the distribution mismatch⁴. Future work includes establishing the appropriate approach to partitioning other distributions with similar challenges such as Poisson Disc.

Acknowledgements

This work was supported in part by the Engineering and Physical Sciences Research Council, grant EP/T013133/1, by the Royal Academy of Engineering, grant RF201617/16/23, and by the Wellcome Trust, grant 203139/Z/16/Z. The computational aspects of this research were supported by the Well-come Trust Core Award Grant Number 203141/Z/16/Z and the NIHR Oxford BRC. The views expressed are those of the authors and not necessarily those of the NHS, the NIHR or the Department of Health. This research was undertaken, in part,thanks to funding from the Canada Research Chairs Program.

References

[1] Jonathan I Tamir, X Yu Stella, and Michael Lustig, “Unsupervised deep basis pursuit: Learning reconstruction without ground-truth data,” in ISMRM annual meeting, 2019.

[2] Hemant Kumar Aggarwal, Aniket Pramanik, and Mathews Jacob, “Ensure: Ensemble stein’s unbiased risk estimator for unsupervised learning,” in IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2021, pp. 1160–1164.

[3] Liu, Jiaming, et al. "RARE: Image reconstruction using deep priors learned without groundtruth." IEEE Journal of Selected Topics in Signal Processing, 2020, pp. 1088-1099.

[4] Burhaneddin Yaman, Seyed Amir Hossein Hosseini, Steen Moeller, Jutta Ellermann, Kâmil Uğurbil, and Mehmet Akçakaya, “Self-supervised learning of physics-guided reconstruction neural networks without fully sampled reference data,” Magnetic resonance in medicine, vol. 84, no. 6, pp. 3172–3191, 2020.

[5] Nick Moran, Dan Schmidt, Yu Zhong, and Patrick Coady, “Noisier2Noise: Learning to denoise from un-paired noisy data,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2020, pp. 12064–12072.

[6] Charles Millard and Mark Chiew, “A framework for self-supervised MR image reconstruction using sub-sampling via Noisier2Noise,” arXiv preprint arXiv:2205.10278, 2022

[7] J. Zbontar, F. Knoll, A. Sriram, T. Murrell, Z. Huang, M. J. Muckley, A. Defazio, R. Stern, P. Johnson, M. Bruno, et al., “fastMRI: Anopen dataset and benchmarks for accelerated MRI,” arXiv preprint arXiv:1811.08839, 2018

[8] K. Hammernik, T. Klatzer, E. Kobler, M. P. Recht, D. K. Sodickson,T. Pock, and F. Knoll, “Learning a variational network for reconstructionof accelerated MRI data,” Magnetic resonance in medicine, vol. 79, no. 6, pp. 3055–3071, 2018

[9] A. Sriram, J. Zbontar, T. Murrell, A. Defazio, C. L. Zitnick, N. Yakubova, F. Knoll, and P. Johnson, “End-to-end variational networks for accelerated MRI reconstruction,” in International Conference on Medical Image Computing and Computer-Assisted Intervention, pp. 64–73, Springer, 2020

[10] Deshpande, Vibhas, et al. "Optimized Caipirinha acceleration patterns for routine clinical 3D imaging." in ISMRM annual meeting, 2012

[11] M. Blumenthal, G. Luo, M. Schilling, M. Haltmeier, and M. Uecker, “NLINV-Net: Self-Supervised End-2-End Learning for Reconstructing Undersampled Radial Cardiac Real-Time Data,” in ISMRM annual meeting, 2022

Figures

Figure 1: Partitioning a sampling set $$$\Omega$$$ into two using a second set $$$\Lambda$$$. Since $$$\Lambda$$$ consists of independently sampled columns, like $$$\Omega$$$, $$$A$$$ and $$$B$$$ are also independently sampled columns. Here, $$$\Omega$$$ and $$$\Lambda$$$ have sub-sampling factors 4 and 2 respectively.

Figure 2: An example of the three types of sampling masks used in this work at sub-sampling factor 4. All three distributions were fully sampled in a central region of width 10. All images are cropped to a central $$$320 \times 320$$$ region. Row sampling was used to evaluate the effect explored in this abstract, not as a suggested sampling scheme for a k-space of such dimension in practice.

Figure 3: The percentage difference between the test set less and the loss of the fully supervised benchmark for various combinations of types of $$$\Lambda$$$ and $$$\Omega$$$ at $$$R\in \{4,8\}$$$. The best performances are for the lowest values, which are shown in the darkest green. SSDU's best performance is when the distribution of $$$\Lambda$$$ is matched with $$$\Omega$$$, with a test set loss within 2% of the fully supervised benchmark.

Figure 4: Example reconstructions at $$$R=4$$$. The best performance in each row is when $$$\Lambda$$$ matches $$$\Omega$$$. For 1D $$$\Omega$$$, the second best performance is when $$$\Lambda$$$ is Bernoulli, performing reasonably well qualitatively despite the distribution mismatch.

Figure 5: Example reconstructions at $$$R=8$$$. The improvement in reconstruction quality when $$$\Omega$$$ and $$$\Lambda$$$ are matched is especially prominent at higher acceleration factors.

Proc. Intl. Soc. Mag. Reson. Med. 31 (2023)

0830

DOI: https://doi.org/10.58530/2023/0830