0828

Multi-echo MRI Reconstruction with Iteratively Refined Zero-shot Spatio-Temporal Deep Generative Prior

Tae Hyung Kim^1,2,3, Jaejin Cho^2,3, Borjan Gagoski^3,4, Zijing Dong^2,3, Fuyixue Wang^2,3, So Hyun Kang¹, and Berkin Bilgic^2,3,5
¹Department of Computer Engineering, Hongik University, Seoul, Korea, Republic of, ²Athinoula A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Boston, MA, United States, ³Department of Radiology, Harvard Medical School, Boston, MA, United States, ⁴Fetal-Neonatal Neuroimaging & Developmental Science Center, Boston Children’s Hospital, Boston, MA, United States, ⁵Harvard/MIT Health Sciences and Technology, Cambridge, MA, United States

Synopsis

Keywords: Image Reconstruction, Brain

The subspace method has been widely used for multi-echo/contrast MRI reconstruction, assuming the temporal MR signal evolution can be compactly represented using a few linear coefficients. Recently, methods based on artificial neural networks (trained with large datasets) enabled nonlinear representations of temporal or spatio-temporal MR signals and demonstrated improved performance. This work proposes a novel zero-shot spatio-temporal generative prior for multi-echo/contrast MRI reconstruction, assuming the spatio-temporal MR signals can be nonlinearly generated using deep generative neural networks without external training data. The proposed method was evaluated with 3D-QALAS and EPTI data, and exhibited substantial improvement in NRMSE against existing methods.

Introduction

Conventional joint reconstruction methods of multi-echo/contrast MRI have been developed based on the subspace methods (1–5) and have provided robust reconstruction. They rely on the premise that nonlinear temporal signal evolutions have linearly compressible representations using a few linear basis vectors. More recent works have proposed to improve them by exploiting the nonlinear representations through artificial neural networks (ANNs) (6–9), which often utilize pre-trained ANNs learned from external training data.
In this work, we introduce a method for joint multi-echo/contrast reconstruction employing nonlinear representation without necessitating external training data. Our method assumes that spatio-temporal MR signals can be nonlinearly generated using deep generative neural networks (GNNs) (10–17) from random representations (noise). The proposed method is iteratively refined by 1. updating multi-echo images based on the generated images from GNN, and 2. training/fine-tuning GNN parameters using the updated multi-echo images. As such, the GNN training is “zero-shot” which does not require external training data.

Code: https://anonymous.4open.science/r/Multiecho_Recon_Deep_Generative_Prior-8403/

Theory

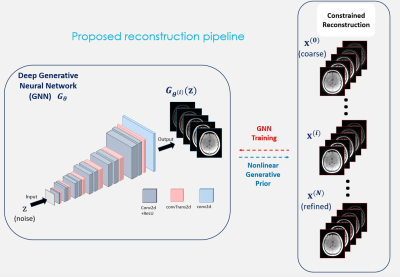
The model for multi-echo/contrast MRI data acquisition can be written as $$\mathbf{y} = \mathbf{A}\mathbf{x} + \mathbf{n}$$ with the acquired raw MR data $$$\mathbf{y}$$$, the forward model $$$\mathbf{A}$$$ (Fourier, coil sensitivity, and undersampling), the multi-echo/contrast MR images $$$\mathbf{x}$$$, and the (thermal) noise $$$\mathbf{n}$$$. The subspace model (1–5) assumes that $$$\mathbf{x}$$$ can be expressed as $$\mathbf{x} \approx \mathbf{\Phi} \mathbf{\alpha}$$ with a compressed linear representation $$$\mathbf{\alpha}$$$ with respect to the linear subspace $$$\mathbf{\Phi}$$$ pre-trained from temporal dictionaries. The corresponding objective function leads to $$\hat{\mathbf{x}}, \hat{\mathbf{\alpha}} = \arg\min_{\mathbf{x},\mathbf{\alpha}} ||\mathbf{y}-\mathbf{A}\mathbf{x}||^2 + \lambda || \mathbf{x} - \mathbf{\Phi} \mathbf{\alpha}||^2$$ or equivalently with $$$\lambda\rightarrow\infty$$$, $$\hat{\mathbf{\alpha}} = \arg\min_\mathbf{\alpha} ||\mathbf{y}-\mathbf{A}\mathbf{\Phi} \mathbf{\alpha}||^2$$ Instead of the linear subspace, we assume that the multi-echo MR Images can be nonlinearly generated from a random representation using a generative artificial neural network (GNN) (10–17).
$$\mathbf{x} \approx G_\mathbf{\theta}(\mathbf{z})$$ with the GNN $$$G_\theta$$$ parameterized by $$$\theta$$$, a random (representation) vector $$$\mathbf{z}$$$. The corresponding objective function becomes $$\hat{\mathbf{x}}, \hat{\mathbf{\theta}} = \arg\min_{\mathbf{x},\mathbf{\theta}} ||\mathbf{y}-\mathbf{A}\mathbf{x}||^2 + \lambda ||\mathbf{x} - G_\mathbf{\theta}(\mathbf{z})||^2$$ where $$$\hat{x}, \hat{\theta}$$$ are solved iteratively via alternating minimization, $$\mathbf{x}^{(i+1)} = (\mathbf{A}^H \mathbf{A} + {\lambda} \mathbf{I})^{-1} (\mathbf{A}^H \mathbf{y} + {\lambda} G_{\mathbf{\theta}^{(i)}} (\mathbf{z}) )$$ $$\mathbf{\theta}^{(i+1)} = \arg\min_\mathbf{\theta} ||\mathbf{x}^{(i+1)} - G_\theta(\mathbf{z})||^2$$ The first step can be solved numerically using the conjugate-gradient (CG), and the second is the GNN training through the Adam optimizer. Accordingly, the generator network $$$G_\mathbf{\theta}$$$ is trained and iteratively fine-tuned using the updated images $$$\mathbf{x}^{(i+1)}$$$, which therefore does not require external data for training. Fig. 1 illustrates the proposed deep generative neural network and the overall reconstruction procedure.

Methods

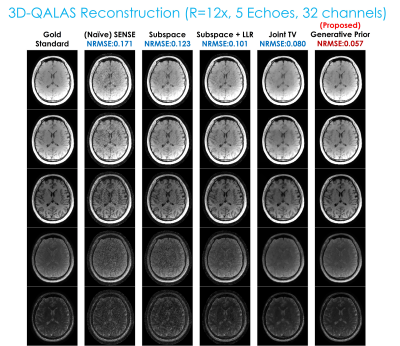
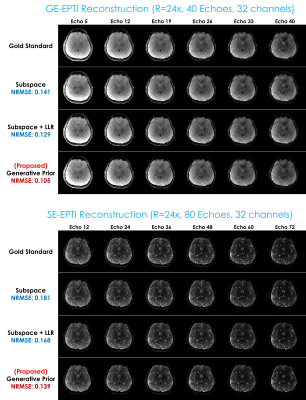
For evaluation, we prepared two multi-echo datasets from Siemens 3T Prisma with 32-channel head coils. One is the 3D-QALAS (3D-quantification using an interleaved look–locker acquisition sequence with a T2 preparation pulse) (18–20) dataset (of which sequence comprises five readouts where the first readout succeeds a T2-preparation module and the remaining four readouts follow an inversion pulse that captures T1 dynamics, enabling joint T1, T2, M0 estimation), with matrix size = 208x208x176, in-plane resolution = 1.15x1.15mm and slice thickness = 1.15mm with 5 echoes. The data was elliptically scanned and retrospectively undersampled using 2D random undersampling masks with the effective acceleration factor R=12x (total 16x with the elliptical sampling), and a single axial readout slice was taken for evaluation. The reconstruction methods used for comparison were Naive SENSE, the subspace method (1–5), the subspace method with a locally low-rank constraint (5,21), joint total variation (22), and the proposed zero-shot deep generative prior.
The second dataset is EPTI (echo-planar time-resolved imaging) (23,24) acquired with matrix size= 216x216, slice thickness = 3mm, in-plane resolution = 1.1x1.1mm, echo spacing = .93 ms, with 40 gradient echoes and 80 spin echoes. The corresponding effective acceleration factor was R=24x. A comparison was conducted between the subspace method, the subspace method with a locally low-rank constraint, and the proposed technique.

Results

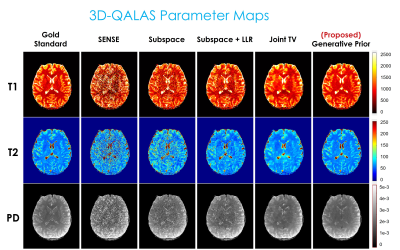
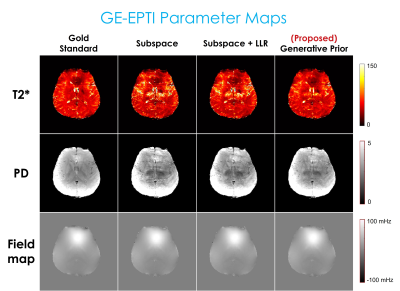
Fig. 2 displays the reconstruction result with 3D-QALAS. Fig. 3 presents the estimated parameter maps (T1, T2, proton density) using the reconstructed images from Fig. 2. Fig. 4 exhibits the gradient-echo EPTI (GE-EPTI) and spin-echo EPTI (SE-EPTI) reconstruction results, and Fig. 5 displays the estimated parameter maps (T2*, proton density, fieldmap) using the reconstructed GE-EPTI images from Fig. 4. All the results indicate that the proposed zero-shot generative prior provides substantial improvement in NRMSE against the conventional multi-echo reconstruction methods.

Discussion and Conclusion

This work proposed multi-echo reconstruction with the zero-shot spatio-temporal deep generative prior, which is an iterative process of 1. training the generator network (GNN) using reconstructed multi-echo images and 2. updating the reconstructed images using the GNN output as the prior. The training of GNN does not require external training data, which is advantageous because obtaining a large set of multi-echo MRI can be particularly difficult. The experiment results with QALAS and EPTI suggest that the proposed approach can be promising for accelerated multi-echo MRI.

Acknowledgements

This work was supported by the National Research Foundation of Korea(NRF) grant funded by the Korea government(MSIT) (No. 2022R1F1A1074786), research grants NIH R01 EB032378, R01 EB028797, R03 EB031175, U01 EB025162, P41 EB030006, U01 EB026996, and the NVidia Corporation for computing support.

References

1. Petzschner FH, Ponce IP, Blaimer M, Jakob PM, Breuer FA. Fast MR parameter mapping using k-t principal component analysis. Magn. Reson. Med. 2011;66:706–716.

2. Huang C, Graff CG, Clarkson EW, Bilgin A, Altbach MI. T2 mapping from highly undersampled data by reconstruction of principal component coefficient maps using compressed sensing. Magn. Reson. Med. 2012;67:1355–1366.

3. Huang C, Bilgin A, Barr T, Altbach MI. T2 relaxometry with indirect echo compensation from highly undersampled data. Magn. Reson. Med. 2013;70:1026–1037.

4. Zhao B, Lu W, Hitchens TK, Lam F, Ho C, Liang Z-P. Accelerated MR parameter mapping with low-rank and sparsity constraints. Magn. Reson. Med. 2015;74:489–498.

5. Tamir JI, Uecker M, Chen W, et al. T2 shuffling: Sharp, multicontrast, volumetric fast spin-echo imaging. Magn. Reson. Med. 2017;77:180–195.

6. Sandino CM, Ong F, Iyer SS, Bush AM, Vasanawala SS. Deep subspace learning for efficient reconstruction of spatiotemporal imaging data. In: NeurIPS 2021 Workshop on Deep Learning and Inverse Problems. Virtual Meeting; 2021.

7. Arefeen Y, Xu J, Zhang M, White J, Bilgic B, Adalsteinsson E. Learning compact latent representations of signal evolution for improved shuffling reconstruction. In: International Society for Magnetic Resonance in Medicine Annual Meeting (ISMRM). London; 2022. p. 0247.

8. Blumenthal M, Wang X, Uecker M. Deep Subspace Learning for Improved T1 Mapping using Single-shot Inversion-Recovery Radial FLASH. In: International Society for Magnetic Resonance in Medicine Annual Meeting (ISMRM). London; 2022. p. 0241.

9. Iyer S, Sandino C, Yurt M, et al. SMILR - Subspace MachIne Learning Reconstruction. In: International Society for Magnetic Resonance in Medicine Annual Meeting (ISMRM). London; 2022. p. 3466.

10. Bora A, Jalal A, Price E, Dimakis AG. Compressed Sensing using Generative Models. In: Proceedings of the 34th International Conference on Machine Learning (ICML). PMLR; 2017. pp. 537–546.

11. Hand P, Voroninski V. Global Guarantees for Enforcing Deep Generative Priors by Empirical Risk. IEEE Trans. Inf. Theory 2020;66:401–418.

12. Huang W, Hand P, Heckel R, Voroninski V. A Provably Convergent Scheme for Compressive Sensing Under Random Generative Priors. J. Fourier Anal. Appl. 2021;27:19.

13. Ma F, Ayaz U, Karaman S. Invertibility of Convolutional Generative Networks from Partial Measurements. In: Advances in Neural Information Processing Systems (NeurIPS). Vol. 31; 2018.

14. Jalal A, Arvinte M, Daras G, Price E, Dimakis AG, Tamir J. Robust Compressed Sensing MRI with Deep Generative Priors. In: Advances in Neural Information Processing Systems (NeurIPS). Vol. 34; 2021. pp. 14938–14954.

15. Ulyanov D, Vedaldi A, Lempitsky V. Deep Image Prior. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 2018. pp. 9446–9454.

16. Heckel R, Hand P. Deep decoder: Concise image representations from untrained non-convolutional networks. In: International Conference on Learning Representations (ICLR) 2019.

17. Darestani MZ, Heckel R. Accelerated MRI With Un-Trained Neural Networks. IEEE Trans. Comput. Imaging 2021;7:724–733.

18. Kvernby S, Warntjes MJB, Haraldsson H, Carlhäll C-J, Engvall J, Ebbers T. Simultaneous three-dimensional myocardial T1 and T2 mapping in one breath hold with 3D-QALAS. J. Cardiovasc. Magn. Reson. 2014;16:102.

19. Kvernby S, Warntjes M, Engvall J, Carlhäll C-J, Ebbers T. Clinical feasibility of 3D-QALAS – Single breath-hold 3D myocardial T1- and T2-mapping. Magn. Reson. Imaging 2017;38:13–20.

20. Fujita S, Hagiwara A, Hori M, et al. Three-dimensional high-resolution simultaneous quantitative mapping of the whole brain with 3D-QALAS: An accuracy and repeatability study. Magn. Reson. Imaging 2019;63:235–243.

21. Zhang T, Pauly JM, Levesque IR. Accelerating parameter mapping with a locally low rank constraint. Magn. Reson. Med. 2015;73:655–661.

22. Chen C, Li Y, Huang J. Calibrationless Parallel MRI with Joint Total Variation Regularization. In: Medical Image Computing and Computer-Assisted Intervention – MICCAI 2013. Berlin, Heidelberg: Springer; 2013. pp. 106–114.

23. Wang F, Dong Z, Reese TG, et al. Echo planar time-resolved imaging (EPTI). Magn. Reson. Med. 2019;81:3599–3615.

24. Dong Z, Wang F, Reese TG, Bilgic B, Setsompop K. Echo planar time-resolved imaging with subspace reconstruction and optimized spatiotemporal encoding. Magn. Reson. Med. 2020;84:2442–2455.

Figures

Fig 1. The proposed GNN network architecture and the iterative reconstruction process. The proposed GNN is initially trained using coarse images from the initial naive reconstruction, then gradually fine-tuned using the updated images in the iterative reconstruction procedure. The generated images from GNN are exploited as the prior to the constrained reconstruction.

Fig. 2. QALAS Reconstruction from 12x-accelerated retrospective random undersampling. The five multi-echo MR images were jointly reconstructed. The methods used for comparisons were CG-SENSE (Naive SENSE), the subspace method (Subspace), the subspace method with locally low-rank constraint (Subspace + LLR), SENSE with joint total variation (Joint TV), and the proposed zero-shot deep generative prior (Generative Prior). The proposed GNN was initialized (initially-trained) using Naive SENSE. The proposed method exhibited the lowest NRMSE (marked as red).

Fig. 3. Parameter maps (T1, T2, proton density) estimated from 3D-QALAS reconstruction in Fig. 2.

Fig. 4. GE-EPTI and SE-EPTI reconstruction results. For GE-EPTI, the 40 gradient-echo images were jointly reconstructed, and six echoes were chosen to be displayed. For SE-EPTI, the 80 spin-echo images were jointly reconstructed, and six echoes were chosen to be displayed. The effective acceleration factor is R=24x. The proposed GNN was initially trained with the subspace reconstruction for each case.

Fig 5. Parameter maps (T2*, proton density, fieldmap) estimated from GE-EPTI reconstruction in Fig. 4.

Proc. Intl. Soc. Mag. Reson. Med. 31 (2023)

0828

DOI: https://doi.org/10.58530/2023/0828