0827
Accelerated MRI Reconstruction using Adaptive Diffusion Probabilistic Networks1Department of Electrical and Electronics Engineering, Bilkent University, Ankara, Turkey, 2National Magnetic Resonance Research Center (UMRAM), Bilkent University, Ankara, Turkey, 3ASELSAN Research Center, Ankara, Turkey, 4Amasya University, Amasya, Turkey, 5Neuroscience Program, Bilkent University, Ankara, Turkey
Synopsis
Keywords: Image Reconstruction, Image Reconstruction
Learning-based MRI reconstruction is commonly performed using non-adaptive models with frozen weights during inference. Non-adaptive conditional models poorly generalize across variable imaging operators, whereas non-adaptive unconditional models poorly generalize across variations in the image distribution. Here, we introduce a novel adaptive method, AdaDiff, that trains an unconditional diffusion prior for high-fidelity image generations and adapts the prior during inference for improved generalization. AdaDiff outperforms state-of-the-art baselines both visually and quantitatively.Introduction
Canonically long exam times in MRI hamper its broad spread utilization in clinical applications. A common solution relies on reconstruction methods that solve an ill-posed inverse problem to recover high-quality images from undersampled MRI acquisitions1,2,3. Deep-learning techniques have empowered leaps in reconstruction performance4,5,6,7,8,9, primarily using conditional models that are trained to de-alias undersampled data with explicit knowledge of the imaging operator4,10,11. Conditional models generalize poorly across domain shifts in the imaging operator (e.g., acceleration rate). For improved generalization, an alternative framework uses unconditional models decoupled the imaging operator to learn generative image priors12,13,14. Recent diffusion probabilistic models are particularly promising in terms of image fidelity15. However, previous methods use static diffusion priors that are frozen during inference on test data, inevitably limiting reliability against domain shifts in the MR image distribution. Here, we introduce a novel adaptive diffusion model, AdaDiff, for accelerated MRI reconstruction. AdaDiff learns an unconditional image prior for high-fidelity image generation, and adapts the prior during inference for enhanced generalization performance. Demonstrations on single- and multi-coil datasets clearly indicate that AdaDiff outperforms competing methods in terms of image quality.Methods
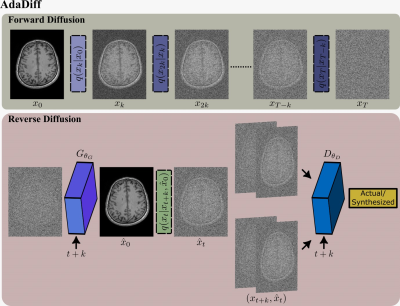
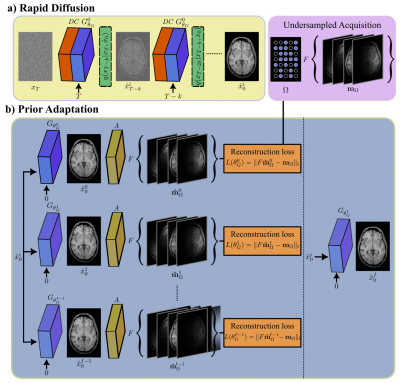
AdaDiff: The proposed model captures a generative image prior based on a rapid temporal Markov process as shown in Fig. 115. Starting with an actual image $$$x_0\approx q(x_0)$$$, each forward diffusion step adds a small amount of Gaussian noise to obtain noisy samples $$$x_{1:T}$$$, eventually converging onto a pure noise sample. Meanwhile, each reverse diffusion step removes the added noise to map the sample from time step $$$t+k$$$ to $$$t$$$. Large diffusion steps are coupled with an adversarial mapper for rapid diffusion sampling16. The adversarial mapper includes a residual convolutional generator to estimate denoised images17 and a convolutional discriminator to learn the distribution of image samples at intermediate steps16.AdaDiff employs a two-phase reconstruction given a learned diffusion prior with a trained generator $$$G_{\theta_G}(\cdot)$$$. (1) The rapid diffusion phase calculates a fast, initial solution as a compromise between consistency with the learned prior and consistency with the imaging operator. Starting with a Gaussian noise sample $$$x_T$$$, interleaved projections are performed through data-consistency (DC) blocks and reverse diffusion steps. The data consistency block solves:
$$\hat{x}_t^i=\min_{Ax_t = y}\left\|\tilde{x}^{G}_{t}-x_t\right\|_{2}^2,$$ where $$$\tilde{x}^{G}_{t}$$$ is the image generated at each step, A is the imaging operator, y are acquired data. The sample at time step 0 is taken as the initial reconstruction, $$$\hat{x}^i_0$$$. (2) The adaptation phase refines the diffusion prior per test subject to further improve the initial reconstruction. To do this, the generator parameters ($$$θ_G$$$) are iteratively optimized to minimize the data consistency loss between synthesized and acquired k-space data:
$$L(\theta_G)=\Vert\hat{m}_\Omega^i–m_\Omega\Vert_1,$$ where $$$\hat{m},m$$$ are synthetic and actual images subjected to the sampling mask $$$\Omega$$$ and $$$\hat{m}_\Omega^i$$$ corresponds to k-space representation of the image generated at step i.
Datasets: Demonstrations were performed on single-coil IXI18 and multi-coil fastMRI19 datasets. Training, validation and test sets included (21,15,30) subjects each with 100 cross-sections in IXI, and (240,60,120) subjects each with 10 cross-sections in fastMRI. Retrospective undersampling was performed with variable-density random masks1.
Modeling Procedures: Models were implemented in PyTorch, training and inference was performed via Adam optimizer. Cross-validated hyperparameters were 6x10-3 learning rate, 500 epochs, T/k=8 diffusion steps for training, 8 reverse diffusion steps for rapid diffusion, and 10-3 learning rate, 1000 iterations for prior adaptation. AdaDiff was compared against 5 state-of-the-art methods: LORAKS3, rGAN10, MoDL11, GANprior12 and DDPM15. Code for AdaDiff is available at https://github.com/icon-lab/AdaDiff.
Results
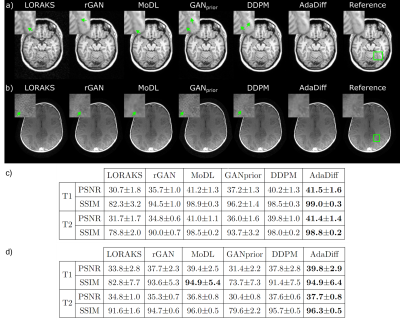
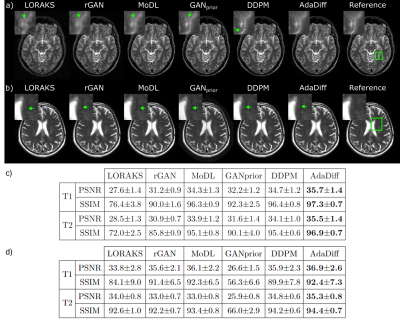
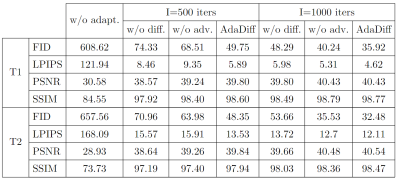
AdaDiff was demonstrated for within-domain reconstruction based on R=4x acceleration in the training-test sets, and for cross-domain reconstruction based on training at R=4x, testing at R=8x. Representative images and performance metrics are displayed for within-domain reconstruction in Fig. 3, and cross-domain reconstruction in Fig. 4. In general, AdaDiff outperforms competing methods quantitatively, and it achieves lower artifact and noise levels along with the highest similarity to the reference images. While MoDL performs competitively in within-domain cases, it suffers from visual blurring. Furthermore, the conditional MoDL method incurs a heavier performance loss in cross-domain cases compared to AdaDiff.Fig. 5 lists performance metrics in ablation studies for the main design elements. AdaDiff was compared against a variant omitting prior adaptation (w/o adapt.), a variant omitting rapid diffusion (w/o diff.), and a variant with a non-adversarial mapper (w/o adv.). AdaDiff outperforms all ablated variants in performance metrics, indicating the importance of each design element.
Discussion
Here, we introduced the first adaptive diffusion model for MRI reconstruction, AdaDiff, that trains a rapid diffusion prior base on an adversarial mapper for efficient image sampling. During inference, rapid projection through the trained diffusion followed by prior adaptation to individual test subjects provides the final reconstruction. Compared to state-of-the-art methods, AdaDiff performs yields superior or on par performance in within-domain tasks, and achieves superior performance in cross-domain tasks. Therefore, AdaDiff holds great promise for performant and generalizable MRI reconstruction.Acknowledgements
This study was supported in part by a TUBITAK BIDEB scholarship awarded to A. Gungor, by a TUBITAK BIDEB scholarship awarded to S. Ozturk, and by a TUBITAK 1001 Research Grant (121E488), a TUBA GEBIP 2015 fellowship, and a BAGEP 2017 fellowship awarded to T. Çukur.References
[1] Lustig, M., Donoho, D., Pauly, J.M., 2007. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magnetic Resonance in Medicine 58, 1182–1195.
[2] Gu, H., Yaman, B., Ugurbil, K., Moeller, S., Akçakaya, M., 2021. Compressed sensing MRI with ℓ1-wavelet reconstruction revisited using modern data science tools, in: 2021 43rd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), IEEE. pp. 3596–3.
[3] Haldar, J.P., Zhuo, J., 2016. P-LORAKS: Low-Rank Modeling of Local k-Space Neighborhoods with Parallel Imaging Data. Magnetic resonance in medicine 75, 1499.
[4] Hammernik, K., Klatzer, T., Kobler, E., Recht, M.P., Sodickson, D.K., Pock, T., Knoll, F., 2017. Learning a variational network for reconstruction of accelerated MRI data. Magnetic Resonance in Medicine 79, 3055–3071.
[5] Jalal, A., Arvinte, M., Daras, G., Price, E., Dimakis, A.G., Tamir, J., 2021. Robust compressed sensing MRI with deep generative priors, in: Advances in Neural Information Processing Systems, pp. 14938–14954.
[6] Liu, Q., Yang, Q., Cheng, H., Wang, S., Zhang, M., Liang, D., 2020. Highly undersampled magnetic resonance imaging reconstruction using autoencoding priors. Magnetic Resonance in Medicine 83, 322–336.
[7] Mardani, M., Gong, E., Cheng, J.Y., Vasanawala, S., Zaharchuk, G., Xing, L., Pauly, J.M., 2019. Deep generative adversarial neural networks for compressive sensing MRI. IEEE Transactions on Medical Imaging 38, 167–179.
[8] Luo, G., Heide, M., Uecker, M., 2022. MRI reconstruction via data driven Markov chain with joint uncertainty estimation. arXiv:2202.01479.
[9] Liang, D., Cheng, J., Ke, Z., Ying, L., 2020. Deep magnetic resonance image reconstruction: Inverse problems meet neural networks. IEEE Signal Processing Magazine 37, 141–151.
[10] Dar, S.U., Yurt, M., Shahdloo, M., Ildız, M.E., Tınaz, B., Çukur, T., 2020a. Prior-guided image reconstruction for accelerated multi-contrast MRI via generative adversarial networks. IEEE Journal of Selected Topics in Signal Processing 14, 1072–1087.
[11] Aggarwal, H.K., Mani, M.P., Jacob, M., 2019. MoDL: Model-Based deep-learning architecture for inverse problems. IEEE Transactions on Medical Imaging 38, 394–405.
[12] Narnhofer, D., Hammernik, K., Knoll, F., Pock, T., 2019. Inverse GANs for accelerated MRI reconstruction, in: Proceedings of SPIE, pp. 381 – 392.
[13] Peng, C., Guo, P., Zhou, S.K., Patel, V., Chellappa, R., 2022. Towards performant and reliable undersampled mr reconstruction via diffusion model sampling. arXiv:2203.04292.
[14] Chung, H., Sim, B., Ye, J.C., 2022. Come-closer-diffuse-faster: Accelerating conditional diffusion models for inverse problems through stochastic contraction, in: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 12413–12422.
[15] Ho, J., Jain, A., Abbeel, P., 2020. Denoising diffusion probabilistic models, in: Advances in Neural Information Processing Systems, pp. 6840–6851.
[16] Xiao, Z., Kreis, K., Vahdat, A., 2022. Tackling the generative learning trilemma with denoising diffusion GANs, in: International Conference on Learning Representations (ICLR).
[17] K. He, X. Zhang, S. Ren and J. Sun, "Deep Residual Learning for Image Recognition," 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016, pp. 770-778, doi: 10.1109/CVPR.2016.90.
[18] IXI Dataset. http://www.brain-development.org/ixi-dataset/.
[19] Knoll, F., Zbontar, J., Sriram, A., Muckley, M.J., Bruno, M., Defazio, A., Parente, M., Geras, K.J., Katsnelson, J., Chandarana, H., Zhang, Z., Drozdzalv, M., Romero, A., Rabbat, M., Vincent, P., Pinkerton, J., Wang, D., Yakubova, N., Owens, E., Zitnick, C.L., Recht, M.P., Sodickson, D.K., Lui, Y.W., 2020. fastMRI: A publicly available raw k-space and DICOM dataset of knee images for accelerated MR image reconstruction using machine learning. Radiology: Artificial Intelligence 2, e190007.
Figures