0820
IMJENSE: scan-specific IMplicit representation for Joint coil sENSitivity and image Estimation in parallel MRI1School of Biomedical Engineering, Shanghai Jiao Tong University, Shanghai, China, 2School of Information Science and Technology, ShanghaiTech University, Shanghai, China
Synopsis
Keywords: Image Reconstruction, Machine Learning/Artificial Intelligence, implicit neural representation
Current parallel imaging techniques for MRI acceleration can still not reliably reconstruct a high-quality image from highly reduced k-space measurements with fewer calibration data. In this study, we applied the new insight of implicit neural representation (INR) to parallel MRI reconstruction. The underlying MRI image and coil sensitivities were modeled as continuous functions of spatial coordinates. These functions were simultaneously learned from the sparsely-acquired k-space itself without additional training data. Thanks to the continuous representation and joint estimation scheme, the proposed method outperforms the existing scan-specific methods, demonstrating its potential for further accelerating the MRI acquisition.
Introduction
The main shortcoming of MRI is the long acquisition time. Current parallel imaging techniques for MRI acceleration still suffer from noise and artifacts at higher acceleration rates with limited auto-calibration signal (ACS) region 1-3. Although deep learning-based methods have shown impressive results, most of these studies rely on a large-scale training database with fully-sampled ground truth data, which hinders their application in practice 4-7. Recently, implicit neural representation (INR) has emerged as a new deep learning paradigm to learn the internal continuity of the desired object 8. Inspired by the new insight of INR, we proposed IMJENSE, a novel framework to jointly reconstruct the MRI image and coil sensitivity maps for parallel MRI. IMJENSE models the underlying MRI image and coil sensitivities as continuous functions of spatial coordinates. These functions were simultaneously learned from the measured k-space itself in a scan-specific fashion. We tested the proposed method on different datasets with different ACS sizes. The experimental results showed that IMJENSE achieved superior performance qualitatively and quantitatively compared with the existing scan-specific methods.Methods
To jointly estimate the MRI image and coil sensitivities, we modeled the sensitivity map as a continuous polynomial function $$$f_\varphi$$$ of the spatial coordinates $$$(x,y)$$$ to further reduce the unknowns in sensitivity maps 9. Let $$$C_j(x,y)$$$ be the value of the $$$j$$$th coil sensitivity at the coordinate $$$(x,y)$$$, then it can be expressed as: $$C_j(x,y)= \sum_{p = 0}^{N} \sum_{q =0}^{N}\varphi_{p,q,j}x^py^q, \tag{1}$$ where $$$\varphi_{p,q,j}$$$ is the unknown polynomial coefficient to be estimated, and $$$N$$$ represents the order of the polynomial. Similarly, the MRI image was also modeled as a continuous function of $$$(x,y)$$$. Since an MRI image consists of more high-frequency information, this image function was parameterized by a multilayer perceptron (MLP) as adopted in the field of INR, i.e., $$$MLP_{\theta}(x,y)$$$, where $$$\theta$$$ denotes the MLP weights to be optimized. Let $$$I(\theta)$$$ and $$$\mathbf{C}_j(\varphi)$$$ be the discretized image vector and sensitivity map matrix after sampling the $$$MLP_{\theta}$$$ and $$$f_\varphi$$$ at the center location of the pixels, respectively. Then the joint reconstruction can be formulated as the following problem that optimizes the parameters in the MLP and polynomial, instead of directly operating on the desired maps: $$\mathop{\arg\min}\limits_{\theta,\varphi}{\frac{1}{2} \sum_{j = 1}^{c} \Vert S_j-\mathbf{MF}\mathbf{C}_j(\varphi)I(\theta) \Vert_2^2 + \lambda \mathcal{R}[I(\theta)]}, \tag{2}$$ where $$$S_j$$$ is the measured k-space signal of the $$$j$$$th coil, $$$\mathbf{F}$$$ denotes the Fourier transform matrix and $$$\mathbf{M}$$$ is the diagonalized sampling mask, $$$c$$$ is the total number of receiver coils, $$$\mathcal{R}[I(\theta)]$$$ is the regularization term that imposes prior knowledge on the output image and $$$\lambda$$$ is a tunable parameter. Since both the MLP and polynomial are continuous functions, they implicitly incorporate the continuity priori on the output maps, resulting in suppressed noise and artifacts.Figure 1 illustrates the overview of IMJENSE. The spatial coordinates are fed into the MLP and polynomial to output the corresponding MRI image and coil sensitivities that are used to match the subsampled measurements in k-space via the forward physical model. The parameters in MLP and polynomial are simultaneously optimized by minimizing the data consistency loss $$$\mathcal{L}_{DC}$$$ and the total variation loss $$$\mathcal{L}_{TV}$$$. When inferring, the estimated k-space data will be replaced by the acquired measurements to enforce k-space self-consistency.
The MLP consists of 8 layers with 256 neurons in the hidden layers. The activation function is the periodic sine function, i.e., SIREN network 10, to enable the network to better learn the high-frequency information in the MRI image. A 15-channel knee dataset from the NYU fastMRI Initiative database 11,12 and a 32-channel brain dataset from the study of Arefeen et al. 13 were retrospectively undersampled to evaluate the proposed method. The GRAPPA 2 algorithm, RAKI 14, and Residual-RAKI 15 were compared.
Results
Figure 2 shows the results on the knee dataset with an acceleration rate of R=4 and 24 ACS lines. IMJENSE effectively removes the noise and aliasing artifacts that are severe on the reconstructed images by the compared methods, as illustrated by the zoomed-in images. Quantitatively, IMJENSE achieves the highest PSNR of 38.57 dB, more than 2 dB higher than Residual-RAKI, and the highest SSIM of 0.9365.Figure 3 shows the results on the human brain dataset with only 8 ACS lines at R=5. IMJENSE significantly improves the quality of reconstructed images. Quantitatively, IMJENSE achieves the highest PSNR of 32.46 dB and the highest SSIM of 0.9731. Figure 4 plots the PSNR variations of these methods as a function of the number of ACS lines. IMJENSE is more robust to the ACS size.
Discussion
IMJENSE can effectively suppress the noise and artifacts in the reconstructed MRI image and is more robust to the ACS size. These superior results can be attributed to the synergy of the internal continuous representation of an image offered by INR and the external regularization term (i.e., the total variation in our study) in the loss function. Additionally, the joint estimation of MRI image and coil sensitivities enables IMJENSE to correct potential inaccuracies in sensitivity maps, thus leading to improved image reconstruction results, especially when the ACS size is extremely small.Conclusion
The high-quality results and the scan-specific characteristic make the proposed method potential for further speeding up the MRI data acquisition.Acknowledgements
This study is supported by the National Natural Science Foundation of China (61901256, 91949120).
References
1. Pruessmann KP, Weiger M, Scheidegger MB, et al. SENSE: Sensitivity encoding for fast MRI. Magnetic Resonance in Medicine. 1999;42(5):952-962.
2. Griswold MA, Jakob PM, Heidemann RM, et al. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magnetic Resonance in Medicine. 2002;47(6):1202-1210.
3. Pruessmann KP, Weiger M, Börnert P, et al. Advances in sensitivity encoding with arbitrary k‐space trajectories. Magnetic Resonance in Medicine. 2001;46(4):638-651.
4. Hammernik K, Klatzer T, Kobler E, et al. Learning a variational network for reconstruction of accelerated MRI data. Magnetic Resonance in Medicine. 2018;79(6):3055-3071.
5. Aggarwal HK, Mani MP, Jacob M. MoDL: Model-based deep learning architecture for inverse problems. IEEE transactions on medical imaging. 2018;38(2):394-405.
6. Kwon K, Kim D, Park H. A parallel MR imaging method using multilayer perceptron. Medical physics. 2017;44(12):6209-6224.
7. Bao L, Ye F, Cai C, et al. Undersampled MR image reconstruction using an enhanced recursive residual network. Journal of Magnetic Resonance. 2019;305:232-246.
8. Mildenhall B, Srinivasan PP, Tancik M, et al. Nerf: Representing scenes as neural radiance fields for view synthesis. Communications of the ACM. 2021;65(1):99-106.
9. Ying L, Sheng J. Joint image reconstruction and sensitivity estimation in SENSE (JSENSE). Magnetic Resonance in Medicine. 2007;57(6):1196-1202.
10. Sitzmann V, Martel J, Bergman A, et al. Implicit neural representations with periodic activation functions. Advances in Neural Information Processing Systems. 2020;33:7462-7473.
11. Knoll F, Zbontar J, Sriram A, et al. fastMRI: A Publicly Available Raw k-Space and DICOM Dataset of Knee Images for Accelerated MR Image Reconstruction Using Machine Learning. Radiology: Artificial Intelligence. 2020;2(1):e190007.
12. Zbontar J, Knoll F, Sriram A, et al. fastMRI: An open dataset and benchmarks for accelerated MRI. arXiv preprint arXiv:181108839. 2018;
13. Arefeen Y, Beker O, Cho J, et al. Scan‐specific artifact reduction in k‐space (SPARK) neural networks synergize with physics‐based reconstruction to accelerate MRI. Magnetic Resonance in Medicine. 2022;87(2):764-780.
14. Akçakaya M, Moeller S, Weingärtner S, et al. Scan-specific robust artificial-neural-networks for k-space interpolation (RAKI) reconstruction: Database-free deep learning for fast imaging. Magnetic Resonance in Medicine. 2019;81(1):439-453.
15. Zhang C, Moeller S, Demirel OB, et al. Residual RAKI: A hybrid linear and non-linear approach for scan-specific k-space deep learning. NeuroImage. 2022;256:119248.
Figures
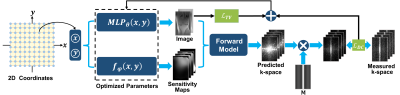
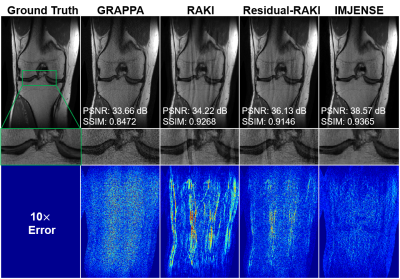
Figure 2. Comparisons of GRAPPA, RAKI, Residual-RAKI, and IMJENSE on the 15-channel knee dataset with 24 ACS lines at R=4. The zoomed-in images show that IMJENSE successfully removes the noise and artifacts. Quantitative evaluation metrics are reported below each image. IMJENSE achieves the highest PSNR and SSIM.
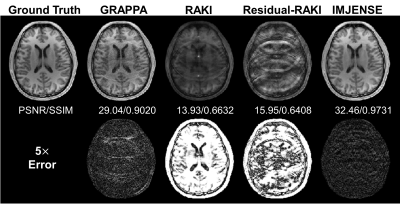
Figure 3. Comparisons of GRAPPA, RAKI, Residual-RAKI, and IMJENSE on the 32-channel human brain dataset with 8 ACS lines at R=5. Quantitative evaluation metrics are reported below each image. IMJENSE achieves the highest PSNR and SSIM.
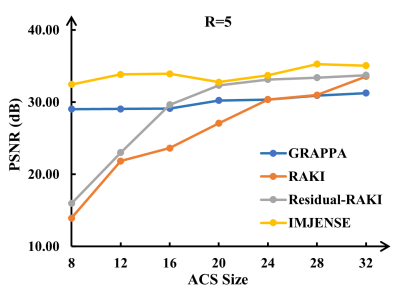
Figure 4. Performance variations of GRAPPA, RAKI, Residual-RAKI, and IMJENSE on the brain dataset as a function of ACS sizes at R=5.