Synopsis

Keywords: Image Reconstruction, Machine Learning/Artificial Intelligence, Image Reconstruction, Heart

Cardiac CINE MR imaging requires long acquisitions under multiple breath-holds. With the development of deep learning-based reconstruction methods, the acceleration rate and reconstructed image quality have been increased. However, existing methods face several shortcomings, such as limited information-sharing across domains and generalizability which may restrict their clinical adoption. To address these issues, we propose A-LIKNet which incorporates attention mechanisms and maximizes information sharing between low-rank, image, and k-space in an interleaved architecture. Results indicate that the proposed A-LIKNet outperforms other methods for up to 24x accelerated acquisitions within a single breath-hold.

Introduction

Cardiac CINE MR imaging allows for accurate and reproducible measurement of cardiac function. Conventionally, multi-slice 2D CINE images are acquired under multiple breath-holds leading to patient discomfort and imprecise assessment. With the development of deep learning-based reconstruction methods, the acceleration rate and reconstructed image quality have been increased.

However, we observe following challenges for learning-based methods:
1. Operation on single domain: image enhancement^1-3, low-rank^4,5, and k-space learning^6,7 focus on reconstruction either in the image or k-space. Although physics-based unrolled networks^8-11 leverage k-space information in the data consistency (DC) layer, k-space information is not learned specifically.
2. Focus on single-domain regularization: most image-based networks^1-3,8-11 ignore the inherent low-rank property of dynamic imaging¹² which can be leveraged^4,5.
3. Equal feature contribution: features along coils or time are treated equally, impairing the representation ability. Attention mechanisms were studied^13-15, but focused on spatial or network-channel-wise attention.
These challenges may limit the full potential of deep learning physics-based reconstruction. Thus we hypothesize that the reachable acceleration rate and reconstructed image quality still have room for improvement.

In this work, we incorporate attention mechanisms in a physics-based unrolled reconstruction network that leverages low-rank, image and k-space information, named A-LIKNet. We maximize the information sharing between domains by parallel k-space and image branches in an interleaved architecture with learnable information-sharing layer (ISL). As dynamic CINE images have a strong low-rank property, both sparse and low-rank priors are learned. Furthermore, attention along time is applied in the image domain to improve dynamic delineation, and attention along coils learns to weigh the coils in k-space domain. Experiments show that the proposed A-LIKNet can effectively reconstruct up to 24x accelerated cardiac CINE images, enabling single breath-hold imaging.

Methods

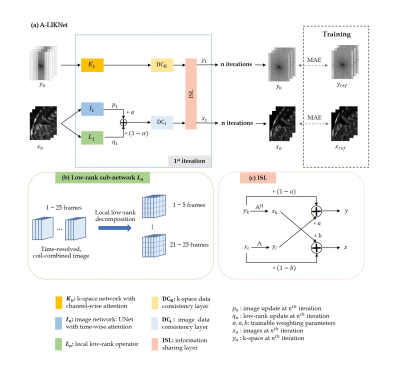
The overall structure of the proposed network is depicted in Fig.1(a), consisting of a k-space branch, an image branch, and ISL.

The network is trained to solve the following problem: $$\mathbf{x}=\arg\,\underset{\mathbf{x}}{\min}\ \frac{1}{2}\parallel\mathbf{Ax}-\mathbf{y}\parallel_{2}^{2}+\lambda_{1}R_{1}\left(\mathbf{x}\right)+\lambda_{2}R_{2}\left(\mathbf{x}\right)$$ which incorporates a sparse $$$R_{1}()$$$ and a low-rank $$$R_{2}()$$$ regularization with weightings $$$\lambda_{1}$$$ and $$$\lambda_{2}$$$ to reconstruct the image $$$\mathbf{x}$$$ from the acquired k-space $$$\mathbf{y}$$$. The encoding operator $$$\mathbf{A}$$$ is composed of the Fourier transformation, undersampling trajectory and coil sensitivities.

The problem is reformulated using variable splitting with auxiliary variables $$$\mathbf{p}$$$ and $$$\mathbf{q}$$$ into the unconstrained Lagrangian function: $$\textit{L}_{\mu_{1},\mu_{2}}(\mathbf{x},\mathbf{p},\mathbf{q})=\frac{1}{2}\parallel\mathbf{Ax}-\mathbf{y}\parallel_{2}^{2}+\lambda_{1}R_{1}\left(\mathbf{p}\right)+\lambda_{2}R_{2}\left(\mathbf{q}\right)+\frac{\mu_{1}}{2}\left\|\mathbf{p}-\mathbf{x}\right\|^{2}_2+\frac{\mu_{2}}{2}\left\|\mathbf{q}-\mathbf{x}\right\|^{2}_2$$ which can be solved iteratively: $$\left\{\begin{matrix}\mathbf{p}_{n+1}={\arg}\,\underset{\mathbf{p}}{\min}\,\frac{\mu_{1}}{2}\left\|\mathbf{p}-\mathbf{x}_{n}\right\|^{2}_2+\lambda_{1}R_{1}\left(\mathbf{p}\right)\\\mathbf{q}_{n+1}={\arg}\,\underset{\mathbf{q}}{\min}\,\frac{\mu_{2}}{2}\left\|\mathbf{q}-\mathbf{x}_{n}\right\|^{2}_2+\lambda_{2}R_{2}\left(\mathbf{q}\right)\\\mathbf{x}_{n+1}={\arg}\,\underset{\mathbf{x}}{\min}\,\frac{1}{2}\left||\mathbf{Ax}-\mathbf{y}\right\|_{2}^{2}+\frac{\mu_{1}}{2}\left\|\mathbf{p}_{n+1}-\mathbf{x}\right\|^{2}+\frac{\mu_{2}}{2}\left\|\mathbf{q}_{n+1}-\mathbf{x}\right\|^{2}\end{matrix}\right.$$ with the sub-problems being formulated as learnable regularizers: $$\left\{\begin{matrix}\mathbf{p}_{n+1}=\textbf{I}_{n+1}(\mathbf{x}_{n})\\\mathbf{q}_{n+1}=\textbf{L}_{n+1}(\mathbf{x}_{n})\\\mathbf{x}_{n+1}=\textbf{DC}_\text{I}(\alpha\cdot\mathbf{p}_{n+1}+(1-\alpha)\cdot\mathbf{q}_{n+1},\mathbf{A},\mathbf{y})\end{matrix}\right.$$ for an image sub-network $$$\textbf{I}_n$$$, low-rank sub-network $$$\textbf{L}_n$$$ weighted by a trainable parameter $$$\alpha=\frac{\mu_{1}}{\mu_{1}+\mu_{2}}$$$ (initialized at 0.5) in a data consistency layer $$$\textbf{DC}_\text{I}$$$ (gradient descent) in image domain.

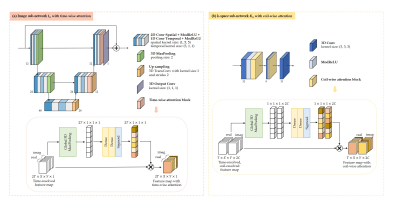
The image sub-network $$$\textbf{I}_{n}$$$ (Fig.2(a)) is expressed as a complex-valued residual 2D+t UNet with attention blocks along time in the decoder. Specifically, time-resolved and spatial-channel-squeezed information is extracted and encoded by one 3D pooling and two fully-connected layers to generate the attention map which will excite the decoder features.

The low-rank sub-network $$$\textbf{L}_{n}$$$ (Fig.1(b)) learns singular value thresholds $$$\lambda_{i}$$$ for local spatial-temporal patches of 4x4 neighbourhood in 5 frames, following¹³: $$\textbf{L}(\mathbf{x}_{n})=\mathbf{U}\cdot\operatorname{diag}\left(\max\left(\operatorname{sigmoid}\left(\lambda_{i}\right)\ast\max\left(\sigma_{in}\right),\sigma_{in}\right)\right)\cdot\mathbf{V}^{H}$$ with singular values of $$$i^{th}$$$ patch $$$\sigma_{in}\,(1\le n\le \operatorname{rank}\left(\mathbf{x}_{i}\right)$$$) to update the whole time sequence $$$\mathbf{q}$$$ which is merged with the image update $$$\mathbf{p}$$$ by $$$\alpha$$$. $$$\textbf{DC}_\text{I}$$$ performs gradient descent data consistency on this combined output to update the image branch.

The k-space sub-network (Fig.2(b)) uses attention along coils in a three-layer architecture with 3D complex-valued convolutions along spatial-temporal dimensions and a null-space projection in k-space $$$\mathbf{DC}_\text{K}$$$.

While local information is captured by the image branch, feature information on a global scale and across coils is captured in the k-space branch. Outputs of the k-space and image branch (after data consistency) are combined in an information sharing layer (Fig.1(c)). Data cross-over between domains is encoded via the respective forward and adjoint encoding operators and weighted by a trainable parameter.

Investigations are carried out on 2D cardiac CINE (bSSFP, TE/TR=1.06/2.12ms, $$$\alpha$$$=52°, resolution=1.9x1.9mm², slice thickness=8mm) acquired on a 1.5T MRI in 129 subjects (38 healthy subjects and 91 patients). Data were split into 115 training and 14 unique test subjects. VISTA¹⁶ undersampling with random acceleration factors 2x to 24x is used. The proposed network was trained with Adam (learning rate=$$$10^{-4}$$$, batch size=1). The proposed method is compared to compressed sensing ($$$l_{1}$$$-wavelet regularization)¹⁷ and MoDL⁹. Furthermore, the effect of the k-space branch is investigated in the A-LINet, i.e. representing the network without k-space branch.

Results and Discussion

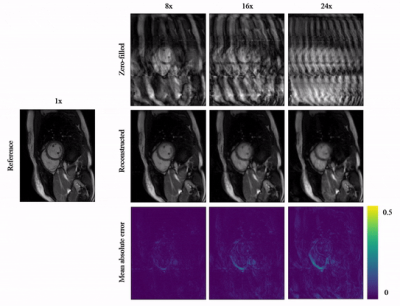
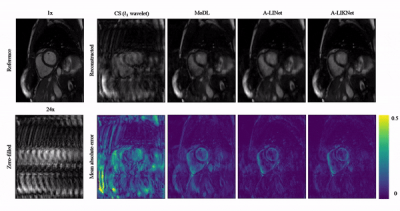
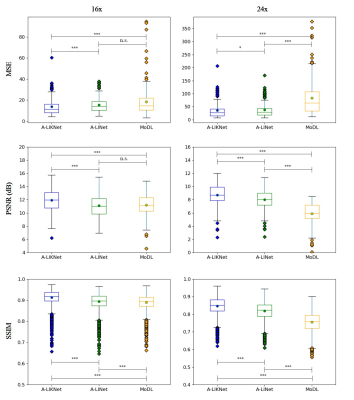
Animated Fig.3 shows reconstructions with the proposed A-LIKNet for 8x, 16x and 24x undersampled 2D cardiac CINE of one patient with active myocarditis, respectively. We can observe stable and effective reconstruction under different accelerations.

A comparison to other methods and the ablated A-LINet is shown in Fig.4 for 24x acceleration. CS can hardly reconstruct images under this high acceleration rate. A-LIKNet shows less error than MoDL, and presents sharper details with improved contrast compared to A-LINet. Fig.5 evaluates the quantitative assessment (MSE, PSNR, SSIM) for MoDL, A-LINet, and A-LIKNet over all test subjects under 16x and 24x acceleration. The proposed A-LIKNet outperforms other networks regarding all metrics.

Conclusion

The proposed A-LIKNet with attention mechanism and ISL maximizes the information sharing between both image/k-space and spatial-temporal domains. As a result, A-LIKNet can efficiently reconstruct 2D cardiac CINE under high acceleration that would enable single breath-hold imaging.

Acknowledgements

S.G. and T.K. contributed equally.