0810
Exploiting the inter-rater disagreement to improve probabilistic segmentation1Faculty of Computer Science, Otto von Guericke University Magdeburg, Magdeburg, Germany, 2Data and Knowledge Engineering Group, Otto von Guericke University Magdeburg, Magdeburg, Germany, 3Department of Biomedical Magnetic Resonance, Otto von Guericke University Magdeburg, Magdeburg, Germany, 4Laboratory of Fluid Dynamics and Technical Flows, Otto von Guericke University Magdeburg, Magdeburg, Germany, 5MedDigit, Department of Neurology, Medical Faculty, University Hospital Magdeburg, Magdeburg, Germany, 6German Center for Neurodegenerative Disease, Magdeburg, Germany, 7Center for Behavioral Brain Sciences, Magdeburg, Germany, 8School of Mathematics & Statistics, University of New South Wales, Sydney, Australia
Synopsis
Keywords: Segmentation, Brain
Disagreements among the experts while segmenting a certain region can be observed for complex segmentation tasks. Deep learning based solution Probabilistic UNet is one of the possible solutions that can learn from a given set of labels for each individual input image and then can produce multiple segmentations for each. But, this does not incorporate the knowledge about the segmentation distribution explicitly. This research extends the idea by incorporating the distribution of the plausible labels as a loss term. The proposed method could reduce the GED by 47% and 63% for multiple sclerosis and vessel segmentation tasks.Introduction
Segmentation of magnetic resonance images can aid in different downstream tasks, like disease progression evaluation, treatment planning, and data assimilation. Manual segmentation can be very time-consuming and can also be ambiguous at times – especially for problems like small vessel segmentation1. Semi-automatic segmentation might achieve good performance but typically require extensive manual fine-tuning. Automatic segmentation using a deep learning model learnt from an expert-annotated dataset can be a suitable solution for segmenting the MRIs without any manual interventions. However, there can also be disagreements among the experts while segmenting a certain region - a problem often seen in tasks like multiple sclerosis2 or locus coeruleus3 segmentations. Probabilistic UNet4 is one of the possible solutions that can learn from a given set of labels for each individual input image and then can produce multiple segmentations for each. In this manner, multiple plausible segmentations can be generated from the same model. However, this does not incorporate the knowledge about the segmentation distribution explicitly that might improve the performance. This research extends the idea of Probabilistic UNet by incorporating the distribution of the interrater disagreement as a loss term.Methods
The probabilistic UNet framework4,5 comprises a segmentation model, in this case, UNet, coupled with a prior encoder net and a posterior encoder net. The input image is supplied to all three models. Additionally, the ground truth is also supplied to the posterior net. Both prior and posterior nets generate respective latent spaces consisting of mean and standard deviation for each. These latent spaces are compared using the Kullback–Leibler divergence6. The posterior net is sampled and supplied into the UNet model to generate a prediction from the input image. This prediction is then compared against a randomly chosen label from the available set of annotations using a loss function, like cross-entropy loss. In the proposed approach, instead of generating one prediction and comparing it against a randomly chosen label, the posterior is sampled n times to generate n segmentations from the UNet, and they are compared against all the n available labels using a distribution distance function. Three different distance functions were evaluated as part of this research - Fréchet inception distance7,8, weighted Hausdorff distance9, and Sinkhorn divergence10.Two datasets for two different tasks were used in this research – vessel segmentation from 7T MRA-ToF – from the StudyForrest dataset11 and multiple sclerosis (MS) segmentation from 3T FLAIR from the MICCAI 2016 challenge dataset2. For the vessel segmentation task, 9, 2, and 4 subjects were used for training, validation, and testing. 10 plausible segmentations for each of the volumes were created in a semi-automatic fashion by manipulating the parameters of the Frangi filter. On the other hand, 32, 7, and 14 subjects were used for training, validation, and testing for the task of MS segmentation, where each volume was annotated by 7 experts. For evaluating the results, the distance between the distribution of the prediction and the ground-truth labels was calculated using generalised energy distance (GED).
Results and Discussion
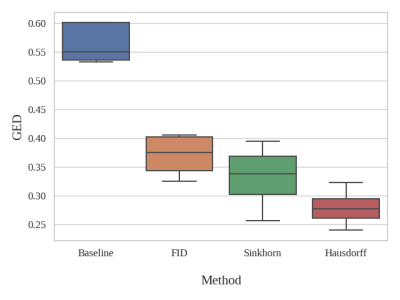
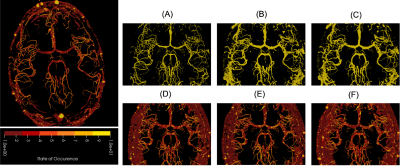
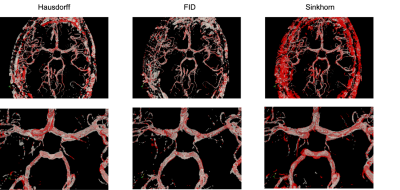
Fig. 1 shows the resultant GEDs for the baselines and the proposed methods for the task of vessel segmentation. The original probabilistic UNet resulted in an average GED of 0.7176. All three abovementioned loss distance losses resulted in lower GED than that, while the best-performing weighted Hausdorff distance resulted in GEDs of 0.2688 – an improvement of nearly 63%. Fig. 2 shows the rate of occurrence of every voxel as a vessel. It can be said that there is only minimal variance in the baseline methods, but the proposed methods’ variance matches the one from the Frangi filter-generated plausible segmentations – the ground-truth in this case. Fig. 3 overlays the two most diverging segmentations as outputs from the proposed methods with different loss functions. In general, for the task of vessel segmentation, it can be said that the proposed methods are able to model the distribution of the plausible labels far better than the baseline probabilistic UNet. For the MS segmentation task, the baseline model resulted in an average GED of 0.8721, while the best-performing proposed method (with weighted Hausdorff distance) resulted in 0.4677 – an improvement of nearly 46%. Fig 4 and 5 show a comparison of the expert annotations and the best-performing proposed method.Conclusion
This research presents a novel method to improve the segmentation quality probabilistic UNet by proposing a distribution-based loss term. During training, the model is sampled n times to generate n outputs, which are then compared against the n available annotations with the help of three different distribution distance functions. The original probabilistic UNet resulted in average GEDs of 0.7176 and 0.87209, respectively, for the tasks of the vessel and multiple sclerosis segmentation. All three proposed loss functions resulted in lower GED than that, while the best-performing weighted Hausdorff distance resulted in GEDs of 0.2688 and 0.46767, respectively. Hence, it can be concluded that distribution distance-based loss functions can help improve the probabilistic segmentation of MRIs with inter-rater disagreements. Further in-depth analyses of the results and applicability to other tasks will be performed in the near future.Acknowledgements
This work was conducted within the context of the International Graduate School MEMoRIAL at Otto von Guericke University (OVGU) Magdeburg, Germany, kindly supported by the European Structural and Investment Funds (ESF) under the programme ”Sachsen-Anhalt WISSENSCHAFT Internationalisierung” (project no. ZS/2016/08/80646) was supported by the federal state of Saxony-Anhalt (“I 88”).References
[1] S. Chatterjee et al., ‘DS6, Deformation-Aware Semi-Supervised Learning: Application to Small Vessel Segmentation with Noisy Training Data’, J. Imaging, vol. 8, no. 10, p. 259, Sep. 2022, doi: 10.3390/jimaging8100259.
[2] O. Commowick et al., ‘Multiple sclerosis lesions segmentation from multiple experts: The MICCAI 2016 challenge dataset’, NeuroImage, vol. 244, p. 118589, Dec. 2021, doi: 10.1016/j.neuroimage.2021.118589.
[3] M. Dünnwald, P. Ernst, E. Düzel, K. Tönnies, M. J. Betts, and S. Oeltze-Jafra, ‘Fully automated deep learning-based localization and segmentation of the locus coeruleus in aging and Parkinson’s disease using neuromelanin-sensitive MRI’, Int. J. Comput. Assist. Radiol. Surg., vol. 16, no. 12, pp. 2129–2135, Dec. 2021, doi: 10.1007/s11548-021-02528-5.
[4] S. Kohl et al., ‘A probabilistic u-net for segmentation of ambiguous images’, Adv. Neural Inf. Process. Syst., vol. 31, 2018.
[5] J. Petersen et al., ‘Deep Probabilistic Modeling of Glioma Growth’, in Medical Image Computing and Computer Assisted Intervention – MICCAI 2019, vol. 11765, D. Shen, T. Liu, T. M. Peters, L. H. Staib, C. Essert, S. Zhou, P.-T. Yap, and A. Khan, Eds. Cham: Springer International Publishing, 2019, pp. 806–814. doi: 10.1007/978-3-030-32245-8_89.
[6] S. Kullback and R. A. Leibler, ‘On Information and Sufficiency’, Ann. Math. Stat., vol. 22, no. 1, pp. 79–86, Mar. 1951, doi: 10.1214/aoms/1177729694.
[7] M. Heusel, H. Ramsauer, T. Unterthiner, B. Nessler, and S. Hochreiter, ‘GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium’, in Advances in Neural Information Processing Systems, 2017, vol. 30.
[8] A. Mathiasen and F. Hvilshøj, ‘Backpropagating through Fr\’echet Inception Distance’. arXiv, Apr. 14, 2021. Accessed: Nov. 09, 2022. [Online]. Available: http://arxiv.org/abs/2009.14075
[9] Yue Lu, Chew Lim Tan, Weihua Huang, and Liying Fan, ‘An approach to word image matching based on weighted Hausdorff distance’, in Proceedings of Sixth International Conference on Document Analysis and Recognition, Seattle, WA, USA, 2001, pp. 921–925. doi: 10.1109/ICDAR.2001.953920.
[10] J. Feydy, T. Séjourné, F.-X. Vialard, S. Amari, A. Trouvé, and G. Peyré, ‘Interpolating between optimal transport and mmd using sinkhorn divergences’, in The 22nd International Conference on Artificial Intelligence and Statistics, 2019, pp. 2681–2690.
[11] M. Hanke et al., ‘A high-resolution 7-Tesla fMRI dataset from complex natural stimulation with an audio movie’, Sci. Data, vol. 1, no. 1, p. 140003, Dec. 2014, doi: 10.1038/sdata.2014.3.
Figures