0772
Two-voxel MRS with B0 correction using a model-based reconstruction
Adam Berrington1 and Olivier Mougin1
1Sir Peter Mansfield Imaging Centre, School of Physics and Astronomy, University of Nottingham, Nottingham, United Kingdom
1Sir Peter Mansfield Imaging Centre, School of Physics and Astronomy, University of Nottingham, Nottingham, United Kingdom
Synopsis
Keywords: Signal Modeling, Spectroscopy
Performing simultaneous MRS from two-regions is often desirable in spectroscopy studies. However, achieving an optimal B0 shim in two regions is difficult, leading to poor data quality. We investigate a model-based reconstruction for two-voxel MRS, incorporating B0 information, to reconstruct data with reduced T2* decay. We test this approach using least squares and regularization approaches for Hadamard encoding in simulations and phantom. Despite a noise penalty for B0-correction (2-4)-fold, FIDs from two voxels better matched un-broadened spectra under conditions of sufficient SNR. Regularization also produced time-domain reconstructions with less noise than a least-squares approach.Introduction
High-quality MRS data are often desired from two regions of interest simultaneously, e.g. as a control region or in functional MRS studies of metabolite response. Using multi-band excitation, simultaneous two-voxel MRS can be achieved with the addition of spatial encoding methods such as Hadamard1, PRIAM2 or recently vGRAPPA3. However, obtaining optimal static shims of the B0 field is difficult across regions4, which limits data quality. To account for B0-induced effects, knowledge of B0 inhomogeneity has previously been incorporated to recover ‘natural linewidth’ spectra in MRSI5. Furthermore, modelling the effect of B0 led to improved reconstruction of SLIM spectra6. In this work, we propose a model-based approach which incorporates the measured B0 inhomogeneity in each region to improve reconstruction of two-voxel Hadamard-encoded MRS data.Theory
To account for the effect of B0 field inhomogeneity, the two-voxel MRS experiment is formulated as a model-based reconstruction. The measured signal, $$$s_{n}(t)$$$, following the $$$n$$$th encode, is a weighted sum of the desired signal, $$$x_{m}(t)$$$, from each voxel, $$$m$$$, such that, $$ s_n(t) = \sum_{m=1}^{2}H_{m,n}x_{m}(t)\int_{R_m}e^{-i[\phi(R) + 2\pi\Delta f(R) t]}dR $$ where $$$H_{m,n}$$$ is the Hadamard encoding applied to the signal in the $$$m$$$th voxel during the $$$n$$$th encode. The time-dependent complex exponential factor accounts for B0-field inhomogeneity through off-resonance, $$$\Delta f(R)$$$, within the spatial region bound by each MRS voxel, $$$R_{m}$$$. Spatial inhomogeneity in the RF transmit phase, $$$\phi(R)$$$, is also included.The acquired signals are concatenated over the two encodings, $$$\textbf{s} = [s_1(t), s_2(t)]^T$$$, and the signal model is reformulated as a matrix equation, such that, $$ \mathbf{s}(t) = \mathbf{G}(t)\mathbf{x}(t) $$ where $$$\mathbf{G}(t)$$$ is the ‘geometry’ matrix containing the Hadamard and time-dependent B0-terms for each voxel and encoding step. This equation can be solved by least squares for each time point in the FID. Additionally, we also investigate a Tikhonov regularization, similar to a previous approach5, such that, $$ \mathbf{x}(t) = \left\| \mathbf{G}(t)\mathbf{x}(t) - \mathbf{s}(t)\right\| + \lambda_t \left\| \mathbf{x}(t)\right\| $$ where $$$\lambda_t$$$ is a regularization parameter and $$$\left\| \cdot \right\|$$$ is the L2 norm.
Methods
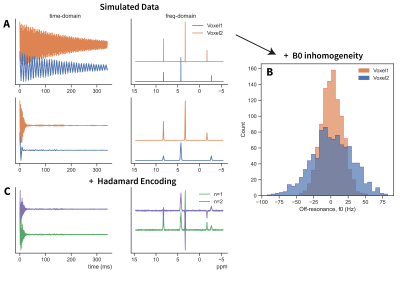
SimulationsSimulations of two-voxel acquisition with 4 different reconstruction approaches were performed considering (i) separate acquisition (SEP), (ii) standard Hadamard reconstruction (H), (iii) a time-dependent least squares solution (B0-LS) and (iv) the regularized approach (B0-REG) (Eq. 3). FIDs from two voxels (V1, V2) were simulated containing different amplitudes and chemical shifts (Fig. 1A). Each voxel comprised of 1000 isochromats with random frequency offsets, $$$\Delta f$$$, drawn from a normal distribution ($$$\sigma_{V1}$$$ = 30 Hz, $$$\sigma_{V2}$$$ = 15 Hz). Complex noise was added over 8 artificial receive channels by sampling from a multivariate normal distribution. Monte-Carlo simulations were performed by incrementing simulated SNR exponentially from 1 to 256 and repeating 10 times. The RMSE of the initial 20% of the reconstructed FIDs were compared to ground-truth (GT) spectra without B0-inhomogeneity. In simulations, the optimal regularization parameter was chosen automatically using the L-curve method7.
Phantom
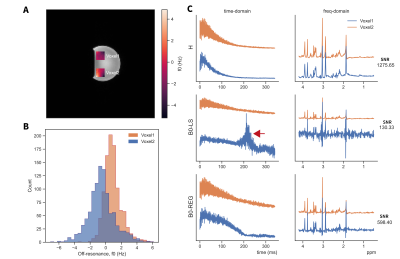
Two-voxel data were also acquired from a homogeneous phantom using a semi-LASER sequence (20x20x20mm3, TE/TR=28ms/6s, NSA=32) on a Philips 7 T MR system (32-channel receive coil) with dual-band RF excitation for Hadamard encoding. Raw data were loaded using NIFTI-MRS8, before being reconstructed using methods (ii-iv) and coil-combined and eddy current corrected9. B0 shimming was performed over the region spanning both voxels and shims were fixed during a subsequent 3D B0-mapping scan (2mm isotropic, delta TE/TR=1/20ms), giving 1000 $$$\Delta f$$$ values per voxel.
Results
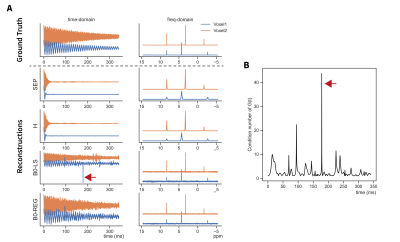
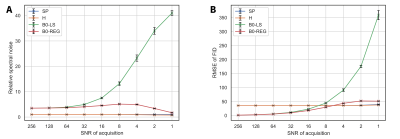
Simulated data were successfully reconstructed from both voxels (Fig 2A). The time-domain reconstruction methods (B0-LS and B0-REG) resulted in visibly reduced B0-induced T2* decay; returning the natural linewidth of the ground truth spectra. At certain time-points, the reconstruction was poorly conditioned (Fig 2B, red arrow), which led to noise amplification using least-squares (B0-LS) but not with the regularized approach (B0-REG). Over all simulated SNR values (Fig 3A), B0-LS reconstruction resulted in a large increase in noise 15x (p<10-18), which was lower for B0-REG 3.8x (p=<10-18). Owing to the absence of T2* decay in the FID, RMSE of B0-REG reconstruction from ground truth spectra was lower than for standard Hadamard reconstruction for SNR values >16 (Fig. 3B).Figure 4 shows the reconstructed phantom data. Despite the fact that each voxel had narrow frequency distribution (2.4 Hz and 4 Hz) (Fig 4B) the reconstructed spectra using B0-REG resulted in visibly narrower linewidths with a noise increase of 2.1x for B0-REG. B0-LS also led to amplification of spurious signal in the middle of the FID.
Discussion & Conclusion
We have demonstrated a model-based approach to account for the effects of B0 inhomogeneity on signals acquired simultaneously using two-voxel MRS. Incorporating knowledge of B0 led to spectra with reduced B0-induced T2* decay, similar to previous work5. The regularized approach resulted in less noise than least-squares reconstruction in simulation (Fig. 2B) and phantom. Despite this, a noise penalty (3-4x in phantom) was still introduced relative to standard reconstruction. Experimental data and simulations (Fig. 3) indicate the method works when SNR is sufficient, however, further work is required to investigate the trade-off between linewidth improvement and noise amplification. B0 inhomogeneity could also be incorporated during spectral fitting and this approach could be applied to other multi-band MRS approaches (SENSE, vGRAPPA) and over multiple regions.Acknowledgements
AB would like to acknowledge the support of the Royal Academy of Engineering.References
[1] M. Dehghani, R. A. E. Edden, and J. Near, “Hadamard-encoded dual-voxel SPECIAL: Short-TE MRS acquired in two brain regions simultaneously using Hadamard encoding,” Magn Reson Med, vol. 87, no. 4, pp. 1649–1660, Apr. 2022, doi: 10.1002/MRM.29129.
[2] V. O. Boer, D. W. J. Klomp, J. Laterra, and P. B. Barker,
“Parallel reconstruction in accelerated multivoxel MR spectroscopy,” Magn
Reson Med, vol. 74, no. 3, pp. 599–606, 2015, doi: 10.1002/mrm.25718.
[3] L. T. Riemann et al., “Fourier-based decomposition
for simultaneous 2-voxel MRS acquisition with 2SPECIAL,” Magn Reson Med,
vol. 88, no. 5, pp. 1978–1993, Nov. 2022, doi: 10.1002/MRM.29369.
[4] V. O. Boer, M. Andersen, A. Lind, N. G. Lee, A. Marsman, and E. T. Petersen, “MR spectroscopy using static higher order shimming with dynamic linear terms (HOS-DLT) for improved water suppression, interleaved MRS-fMRI, and navigator-based motion correction at 7T,” Magn Reson Med, vol. 84, no. 3, pp. 1101–1112, 2020, doi: 10.1002/mrm.28202.
[5] A. Bashir and D. A. Yablonskiy, “Natural linewidth chemical
shift imaging (NL-CSI),” Magn Reson Med, vol. 56, no. 1, pp. 7–18,
2006, doi: 10.1002/mrm.20917.
[6] P. Adany, I. Y. Choi, and P. Lee, “B0-adjusted and
sensitivity-encoded spectral localization by imaging (BASE-SLIM) in the human
brain in vivo,” Neuroimage, vol. 134, pp. 355–364, 2016, doi:
10.1016/j.neuroimage.2016.04.016.
[7] A. Cultrera and L. Callegaro, “A simple algorithm to find
the L-curve corner in the regularisation of ill-posed inverse problems,” IOP
SciNotes, vol. 1, no. 2, p. 025004, Aug. 2020, doi:
10.1088/2633-1357/ABAD0D.
[8] W. T. Clarke et al., “NIfTI-MRS: A standard data
format for magnetic resonance spectroscopy,” Magn Reson Med, Dec. 2022,
doi: 10.1002/MRM.29418.
[9] W. T. Clarke, C. J. Stagg, and S. Jbabdi, “FSL‐MRS: An
end‐to‐end spectroscopy analysis package,” Magn Reson Med, vol. 85, no.
6, pp. 2950–2964, Jun. 2021, doi: 10.1002/mrm.28630.
Figures
Figure 1:
Simulations for two-voxel MRS with Hadamard encoding including the effect of B0
inhomogeneity. Spectra from two regions were simulated (A) and modulated with off-resonance from B0 inhomogeneity (B) drawn from a normal distribution
with standard deviation of 15Hz and 30Hz for Voxel1 and Voxel 2, respectively.
White noise was added and two acquisitions were created to generate a Hadamard
encoding scheme (C).
Figure 2: (A) Example FIDs reconstructed using methods (i-iv) and ground truth data without B0
inhomogeneity (for SNR=50). SEP = separate reconstruction, H = Hadamard reconstruction,
B0-LS = Time-domain least squares with B0 model, B0-REG = Regularized
reconstruction. (B) Plot of the
condition number of the geometry matrix, $$$\mathbf{G}(t)$$$ as a function of time. Red arrow indicates poor conditioning of reconstruction leading to a noisier final spectrum for B0-LS.
Figure 3: Monte Carlo simulations
of reconstruction approaches over different simulated SNR values. (A) Noise in spectral domain (relative to
separate acquisitions) and (B) mean RMSE
between the reconstructed FIDs and ground truth data (over first 20% of time
points). Data were averaged over 10 repetitions for each noise value. Separate
acquisitions (SEP) are shown as if 2 averages were acquired and are similar to Hadamard acquisition. H = Hadamard
reconstruction, B0-LS = Time-domain least squares with B0 model, B0-REG =
Regularized reconstruction.
Figure 4: Two-voxel data acquired from a homogeneous metabolite phantom (A) with 40 mm separation (NSA=32, semi-LASER, TE/TR=28ms/6s, 7T). (B) Histogram of frequency offsets measured in each voxel (orange and blue, FWHM = 2.6 Hz and 4.0 Hz). (C) Reconstruction of data using Hadamard (H), including B0 effects (B0+LS) and the regularised approach (B0-REG) with λ=0.1 (manually chosen). B0-LS lead to amplification of spurious echoes in latter part of FID (red arrow). Average SNR of both spectra are provided.
DOI: https://doi.org/10.58530/2023/0772