Introduction

Quantitative MRI provides parametrical information of biophysical tissue types and microstructural processes. Deep neural networks (DNNs) have shown to be a promising alternative to conventional least squares (LSQ) approaches for this purpose. A common approach is to train these DNNs in a voxelwise-manner^1,2, but does not incorporate spatial information. Traditional fitting methods could promote spatial homogeneity by adding regularization that penalizes differences with neighboring voxels. However, this approach does not consider local structure; hence it may perform poorly wherever there is genuine heterogeneity.

Incorporating spatial homogeneity in the supervision of DNNs is challenging, particularly because LSQ approaches are highly sensitive to noise, and therefore not reliable as ground truth for training. Simulating training data is beneficial in that any possible MRI signal can be generated, and correlations between neighbors can be synthetically introduced in a realistic fashion. In this work, we provide a demonstration of synthetic training data which incorporates spatial information for the intravoxel incoherent motion (IVIM)³ model for diffusion-weighted imaging (DWI). We hypothesize that DNNs can improve IVIM fitting by training on all plausible combinations of correlations with direct neighbors.

Methods

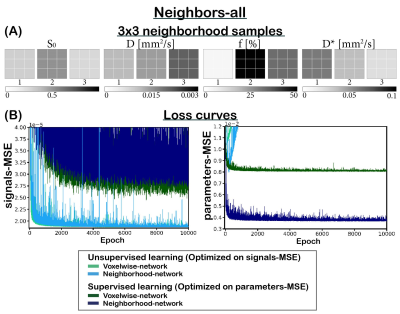
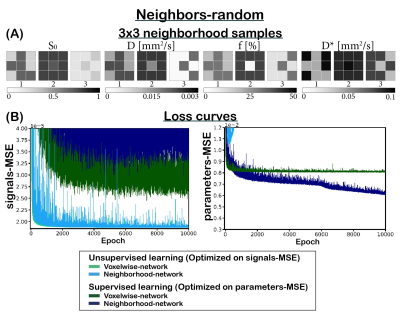
We implemented two multi-layer perceptrons (MLPs; 5 hidden-layers, 256 units). The first (voxelwise) network is a classical MLP, and the second (neighborhood) network takes a 2D-convolution with kernel size 3 in its first layer. The networks input consisted of the DWI signal, and the output consisted of the three IVIM parameters (‘D’ diffusion coefficient, ‘D*’ pseudo-diffusion coefficient, and ‘f’ perfusion fraction) plus S₀. The networks were trained unsupervised or supervised. The unsupervised networks were trained using a loss equal to the mean-squared error (MSE) between the input and estimated IVIM signal (“signals-MSE”). The supervised networks were trained on the MSE between the input and estimated parameters (“parameters-MSE”).

We considered two training sets. (1) IVIM signals were simulated by uniformly sampling 3x3 neighborhoods of parameters between: 0≤S₀≤1, 0×10^-3≤D≤3×10^-3 mm²/s, 0≤F≤50%, and 3×10^-3≤D*≤100×10^-3 mm²/s, considering 16 b values⁴. The parameters of each neighbor of the center pixel were chosen such that a specific number (X) of neighbors had parameters identical to its center (neighbors-X, Figure 3). (2) To simulate a more realistic approach, 3x3 neighborhoods were simulated similar to (1) but each neighborhood consisted of a random number of neighbors correlated to its center (neighbors-random, Figure 2A). Both test sets consisted of 100,000 IVIM signals. Training was performed with learning rate 1×10^-4 for 35,000 epochs. Rician noise was added to the signals, where S₀=1 equates to SNR=200.

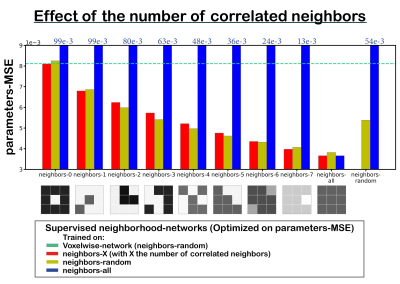
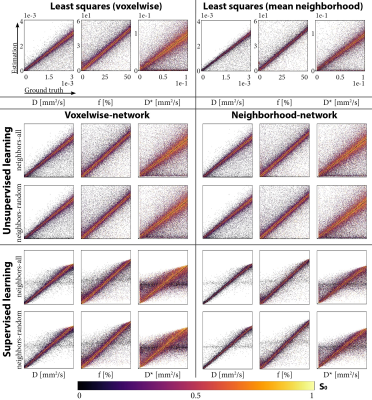
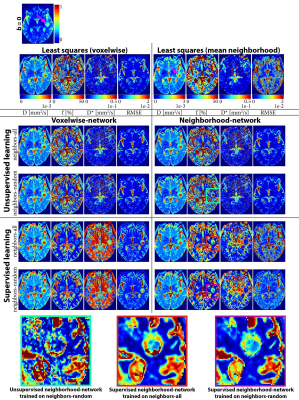
Four networks were evaluated on test sets with all (neighbors-all) or a random number (neighbors-random) of neighbors correlated, trained unsupervised or supervised, and using the voxelwise or neighborhood-network. For each network, we computed the overall signals-MSE and parameters-MSE, and evaluated predictions for individual data points on the neighbors-all test set. Further qualitative assessment was performed on a single IVIM scan of a glioma patient⁴. We also performed a LSQ fit and a LSQ fit on the mean of each 3x3 neighborhood (LSQ-mean). In addition, we evaluated the supervised networks for each number of correlated neighbors individually. As a baseline for what performance can be optimally achieved with the added spatial information, we also trained networks specifically for each number of neighbors.

Results

Incorporating spatial information showed no benefit for unsupervised learning, whereas for supervised learning it resulted in a lower loss and improved precision, particularly for the ideal situation where all neighbors were correlated (Figure 1), but also for the more realistic situation with a random number of correlated neighbors (Figure 2). The networks trained on neighbors-all demonstrated poor generalizability when fewer neighbors were correlated, whereas the network trained on neighbors-random demonstrated results comparable to the baseline optima (Figure 3). Figure 4 further shows that for all unsupervised networks, parameter estimates displayed variability similar to LSQ estimates. Conversely, for supervised learning, incorporating spatial information resulted in comparable performance to LSQ-mean. Although a bias towards the mean of the training distribution persists, it is reduced compared to the voxelwise-networks. Figure 5 qualitatively shows improved performance for the supervised neighborhood-networks in an in vivo scan, where the network trained on neighbors-random preserves edge-like structures better than trained on neighbors-all, while improving RMSE.

Discussion

Incorporating spatial information in deep learning parameter estimation can enhance IVIM fitting, yet only for supervised learning. In this work, we showed that incorporating spatial information for unsupervised learning shows no improvement, which originates from the loss function that minimizes the error on the noisy signal of one single voxel, which essentially mimics LSQ. It remains a question whether performance of unsupervised learning can actually be improved with more advanced architectures⁵. We showed that by generating synthetic data with spatial correlations, we can improve the performance of supervised learning, by detecting relevant neighboring signals and effectively denoising the DWI data while preserving edge-like structures. Training on all plausible combinations of neighboring correlations efficiently utilizes correlations when present, whereas traditional regularization treats all neighbors equally, regardless of similarity to the center voxel. Therefore, synthetic data is a powerful tool to capture spatial information in supervised deep learning. Still, homogeneity between microstructures is expected, and learning such additional relationships from actual images could enhance our approach.

Acknowledgements

This work was supported by the Research Council of Norway (FRIPRO Researcher Project 302624). The second and last authors contributed equally to this work. We gratefully thank Christian Federau for providing the in vivo glioma patient data used in this abstract.