Synopsis

Keywords: Image Reconstruction, Heart, Self-supervised Learning

Physics-guided self-supervised learning (PG-SSL) of MRI reconstruction may provide high spatiotemporal fidelity and fast reconstruction of highly accelerated first-pass myocardial perfusion MRI without ground truth. We sought to develop a SSL model with self-supervised regularization (SSR) using Siamese architecture with stop gradient and re-undersampling block to generate physics-based data augmentation and regularization. PG unrolled network was used as the sub-network in Siamese structure. Self-supervised learning with self-supervised regularization (SSLR) outperformed low rank plus sparse on retrospective rate-8 undersampling single-band data and showed improved SNR and temporal fidelity on prospective multiband whole-heart coverage high resolution perfusion imaging.

Introduction

Highly accelerated first-pass myocardial perfusion MRI is useful for improving assessment of coronary artery disease; however, a tradeoff exists among SNR, spatial and temporal resolution, slice coverage and spatiotemporal fidelity [1] for parallel imaging and compressed sensing. Self-supervised learning (SSL) of MRI reconstruction [2,3,4] has high potential to improve spatiotemporal fidelity without fully-sampled k-space as reference [2,3,4]. However, SSL of physics-guided network (PG-SSL) [5] is challenged by noise amplification [4] using one unrolled network and collapsing [3] using a Siamese structure. Data-splitting based self-supervised reconstruction network has shown the power of physics-guided self-supervised learning in MRI reconstruction. However, data-splitting based method could not utilize all acquired k-space data in the loss function and is restricted to the size of data-splitting mask [5]. We sought to develop a PG-SSL method with self-supervised regularization (SSLR) using a Siamese structure, re-undersampling block and consistency of PG networks. Multiband (MB) technique increases the slice coverage and spatial resolution of myocardial perfusion imaging, but highly accelerated perfusion imaging suffers from low SNR, suboptimal spatiotemporal fidelity and low computation speed. Here we propose SSLR for reconstruction of accelerated single-band (SB) and MB perfusion data. Fast computation, improved SNR and high spatiotemporal fidelity of SSLR may benefit highly accelerated and high-resolution myocardial perfusion imaging.

Methods

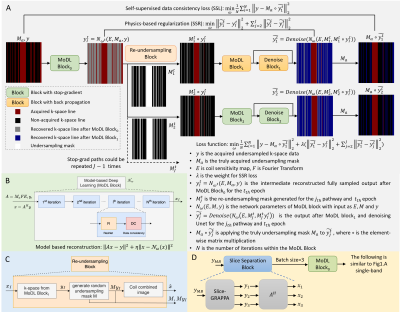
Datasets: Image datasets were acquired on a 1.5T system (Aera, Siemens) using 20-34 RF receiver channels. Twenty-two SB datasets (2640 images) with 2.25mm×2.25mm resolution were acquired using routine saturation-recovery gradient-echo sequence with rate-2 undersampling and reconstructed using GRAPPA. Seven MB datasets (2240 images) were prospectively acquired with 1.5mm×1.5mm resolution. Retrospective rate-8 undersampling data were generated with a 24 lines calibration region. Ten datasets, two datasets and ten datasets were used as training, validation, and testing datasets for SB SSLR. Retrospective rate-8 k-t undersampled datasets were generated and reconstructed using ESPIRiT and L+S methods [1]. Four MB datasets, 4 datasets were used in training and 3 datasets were tested.
Network: SSLR (Fig. 1A) is designed based on 2D Siamese networks, which is composed of two or more identical sub-networks with shared weights. Only one of the sub-networks will update weights during backpropagation, with other networks using stop-gradient. Model-based deep learning block (MoDL) is physics-based unrolled networks with N iterations to reconstruct undersampled images and act as the sub-network structure in Siamese architecture (Fig. 1B). An intermediate reconstructed fully-sampled data was reconstructed after MoDL block₀. A new random re-undersampling mask generated by the Re-undersampling Block in each epoch t (Fig. 1C) was applied to produce augmented undersampled data. An additional Unet was used after MoDL block₁ to control the noise of images reconstructed using re-undersampled data. The loss function was composed of two parts: self-supervised data consistency term between the acquired data and the final output , and the physics-based regularization term among the outputs of the Siamese networks. The first term enables all acquired data being utilized in both of loss function and DC blocks inside the network by means of Re-undersamping Block and stop-gradient. The second term enforces the consistency among physics-guided networks based on coil information. One additional stop-grad path with another re-undersampling mask was used to stabilize the Denoise block. More stop-grad paths could be added to further regularize and stabilize the network consistency. For MB data, slice separation block by slice-GRAPPA was added (Fig. 1D) and the slice dimension was permuted into batch dimension. Phase modulation was used in the MB loss function (Fig.1D).
Assessment: Rate-8 ESPIRiT, L+S and SSLR were compared to rate-2 GRAPPA reconstructed images using normalized RMSE, SSIM of the images, and nRMSE of time curves to quantify spatiotemporal fidelity. MB=3 and R=3 prospectively acquired data were reconstructed using slice-GRAPPA, slice-L+S and slice-SSLR. Both images and temporal time curves were compared.

Results

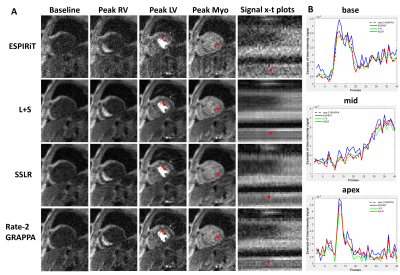
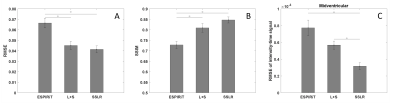
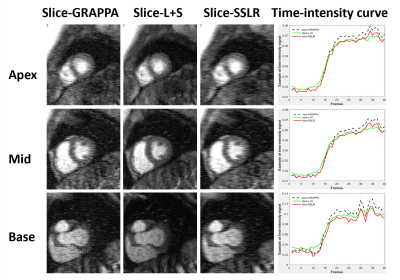
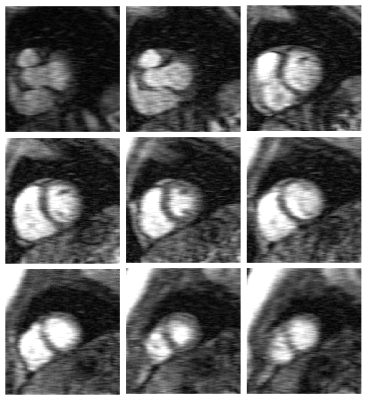
Figure 2 illustrates example images at different time points and signal x-t plots from one patient, where rate-8 ESPIRiT, L+S, SSLR and reference rate-2 GRAPPA images at the mid-ventricular location are shown. SSLR shows higher image quality and has more similar temporal fidelity to reference images than ESPIRiT and L+S (Fig. 2A, B). Quantification of RMSE and SSIM are shown in Figure 3 for all 10 testing datasets. RMSE values were 0.067±0.015, 0.045±0.012 and 0.041±0.010. SSIM values were 0.73±0.05, 0.81±0.07 and 0.85±0.05. RMSE of intensity-time signal were 0.98±0.51, 0.75±0.35 and 0.47±0.28 (*1e-3). Compared with rate-2 GRAPPA images, SSLR shows significantly higher temporal fidelity with the lowest RMSE of time signal (*P<0.05, ANONA), and slightly higher image quality with highest SSIM and lowest RMSE (*P<0.05, ANONA). Figure 4 shows the comparison of slice-GRAPPA, slice-L+S and slice-SSLR for simultaneously acquired three slices. SSLR shows lower noise level, more similar dynamic curve and ~×20 faster computation time than slice-L+S. Nine slices in MB acquisition are reconstructed using SSLR and show good image quality (Figure 5).

Discussion and Conclusions

The proposed SSLR outperformed ESPIRiT and L+S methods in SB reconstruction, and shows high computational efficiency for MB reconstruction, and is a promising method for improving spatiotemporal fidelity, slice coverage and spatial resolution of highly accelerated first-pass perfusion MRI without fully-sampled k-space.

Acknowledgements

We acknowledge the gracious support from UVA team, especially Dr. Frederick Epstein and Dr. Christopher Kramer.