0689
Measuring time-dependent diffusion on a high-performance head-only gradient system at 3T: influence and correction of gradient nonlinearity1Department of Radiology, Stanford University, Stanford, CA, United States, 2GE Research, Niskayuna, NY, United States, 3Department of Electrical Engineering, Stanford University, Stanford, CA, United States, 4Department of Radiology and Imaging, Hospital For Special Surgery, New York, NY, United States
Synopsis
Keywords: Microstructure, Diffusion/other diffusion imaging techniques
Oscillating gradient spin echo (OGSE) sequence is an effective approach to measure time-dependent diffusion processes at short diffusion times. High-performance, head-only gradient systems open new opportunities for using OGSE to study time-dependent diffusion with both high b-values and oscillating frequencies, such as diffusion kurtosis imaging (DKI). One source of error that can be more problematic for the head-only gradients is gradient nonlinearity (GNL). Here, we measure the time dependence of diffusion tensor imaging (DTI)/DKI in human brains with OGSE on a head-only MAGNUS gradient and investigate the influence of GNL on the time dependence measures of diffusivity/kurtosis.
Purpose
Measuring the time/frequency dependence of diffusion MRI at different diffusion length scales is valuable to disentangle the effects of different tissue microenvironments. Oscillating gradient spin echo (OGSE) is an effective approach to measure the time-dependent diffusion process at short diffusion times (Δeff<20 ms) 1, compared with pulsed-gradient spin echo and stimulated echo sequences 2,3. Compared with diffusion tensor imaging (DTI), diffusion kurtosis imaging (DKI) is potentially more sensitive to microstructure changes 4, but measuring time-dependent kurtosis with OGSE requires both high b-values and high encoding frequencies. To meet these requirements, high gradient amplitudes, slew rates, and PNS thresholds are needed, which are difficult to achieve with conventional whole-body gradient systems. Recent developments in high-performance, head-only gradient systems provide new opportunities to study the time-dependent DKI with OGSE 5,6. One source of error that can be more problematic for the smaller inner-diameter head-only gradients compared with the larger inner-diameter whole-body system is gradient nonlinearity (GNL) 7-9. In this study, we (1) measure the time/frequency dependence of diffusivity (Df) with both DTI and DKI models and kurtosis (Kf ) in human subjects in a high-performance, head-only gradient system 10, with a combination of b values, oscillating frequencies, and TE that have not been achieved before; (2) investigate the influence of GNL and GNL correction on diffusivity, kurtosis, and their time dependence measures.Methods
Data Acquisition. Six subjects were scanned on a 3.0 T whole-body magnet (MR750, GE Healthcare) equipped with a head-only MAGNUS gradient (Gmax=200 mT/m, SRmax=500 T/m/s) 11,12 and a 32-channel Nova receive coil. A custom cosine-modulated trapezoid OGSE sequence was used to maximize achievable b-values while maintaining sharp spectral profiles 13. Scans were performed at four frequencies (f=0, 20.9, 35.7, and 47.7 Hz) (effective diffusion times Δeff=14.2, 7.5, 5.2, and 4.0 ms). Detailed imaging parameters are listed in Table 1.Diffusion Analysis. The susceptibility and eddy-current-induced distortion artifacts were first corrected using FSL TOPUP14 and EDDY 15. For each frequency, DTI (with b=1000 s/mm2) and DKI fitting (with b=1000 and 2000 s/mm2) were conducted using the DESIGNER toolbox 16. All diffusion parameter maps were aligned to the f=0 diffusion space using ANTs 17.
GNC. The nominally single b-value and diffusion encoding direction (“b tensor”) were converted to voxel-wise b-value and tensor maps using vendor-provided basis function coefficients 18. The generated voxel-wise b-value and tensor maps were used for DTI and DKI fitting with a custom script based on the DESIGNER toolbox 16.
ROI extraction. Two cortical (pre- and postcentral cortex) and one deep (Thalamus) GM ROIs were segmented with the T1w MPRAGE image (Figure 1A) using FreeSurfer 19 and then co-registered to the f=0 diffusion space using ANTs 17. To avoid partial volume effects, fractional anisotropy (FA) thresholds were imposed on the segmented ROIs (cortex: FA<0.3; deep GM: FA<0.4). The relationships between mean diffusivity (MD) and kurtosis (MK) and frequencies were investigated across different GM ROIs, with and without GNC.
Power-law fitting. At each frequency, the diffusivity/kurtosis values were calculated by first taking the median values in each ROI and then averaging them across all subjects. To determine the relationship between the diffusivity/kurtosis and frequencies, the diffusivity/kurtosis parameters were fitted to the power-law equations 20,
and
$$K=K_{f=0}+\Lambda _{K}f^{\vartheta _{K}},$$
where Df=0/Kf=0 is the diffusivity/kurtosis values at f=0.
Results
An example b=2000 s/mm2 b value map, three diffusion maps (MDDTI, MDDKI, and MK) with and without GNC at f=0 are shown in Figure 1B to 1D. The relative changes (e.g., (MDwGNC- MDwoGNC)/ MDwoGNC×100%) are shown in Figure 1E. The nominal b-value is significantly smaller than the actual values in outer regions (far away from the gradient isocenter), resulting in over-estimated MD values without GNC, as expected. The influence of GNL on MK is much weaker.Table 2 lists the MDDTI, MDDKI, and MK values in three selected GM ROIs (Figure 1A) with and without GNC at different frequencies for a single subject. Consistent with Figure 1, without GNC, MDDTI and MDDKI are over-estimated at all frequencies for pre- and post-central cortex (outer brain), while they are slightly under-estimated in Thalamus (closer to gradient isocenter and thus less GNL effects). No obvious changes are observed for MK for all three ROIs.
Figure 2 plots the MD and MK measures (averaged across different subjects) and power-law fitting curves, with and without GNC. MD and MK show different trends over different frequencies. Table 3 summarizes the power-law fitting results, with and without GNC. Consistent with Table 2, the influence of GNL is severer for MD measurements particularly in outer brain regions (i.e., MDDTI and MDDKI in pre- and post-central cortex).
Discussion & Conclusion
We successfully measured the time dependence of DKI at short diffusion times using OGSE on MAGNUS. The negative correlations between kurtosis and f (or equivalently, positive correlations between kurtosis and Δeff) at short Δeff were captured, consistent with previous simulation and animal studies 3,21. The GNL can affect diffusivity and corresponding time dependence measures significantly, which should be carefully corrected, particularly for outer brain regions (e.g., cortex) in small diameter gradient coils. The influence of GNL on kurtosis measures is less significant partially because of the scaling effects (K~MD2/D2).Acknowledgements
We thank the support from GE Healthcare and the funding from Congressional Directed Medical Research Programs (CDMRP) W81XWH-16-2-0054.
References
1. Does MD, Parsons EC, Gore JC. Oscillating gradient measurements of water diffusion in normal and globally ischemic rat brain. Magn Reson Med 2003;49:206-215.
2. Fieremans E, Burcaw LM, Lee HH, et al. In vivo observation and biophysical interpretation of time-dependent diffusion in human white matter. Neuroimage 2016;129:414-427.
3. Lee HH, Papaioannou A, Novikov DS, Fieremans E. In vivo observation and biophysical interpretation of time-dependent diffusion in human cortical gray matter. Neuroimage 2020;222117054.
4. Jensen JH, Helpern JA, Ramani A, Lu H, Kaczynski K. Diffusional kurtosis imaging: the quantification of non-gaussian water diffusion by means of magnetic resonance imaging. Magn Reson Med 2005;53:1432-1440.
5. Tan ET, Shih RY, Mitra J, et al. Oscillating diffusion-encoding with a high gradient-amplitude and high slew-rate head-only gradient for human brain imaging. Magn Reson Med 2020;84:950-965.
6. Hennel F, Michael ES, Pruessmann KP. Improved gradient waveforms for oscillating gradient spin-echo (OGSE) diffusion tensor imaging. NMR Biomed 2021;34e4434.
7. Newitt DC, Tan ET, Wilmes LJ, et al. Gradient nonlinearity correction to improve apparent diffusion coefficient accuracy and standardization in the american college of radiology imaging network 6698 breast cancer trial. J Magn Reson Imaging 2015;42:908-919.
8. Tao S, Trzasko JD, Gunter JL, et al. Gradient nonlinearity calibration and correction for a compact, asymmetric magnetic resonance imaging gradient system. Phys Med Biol 2017;62:N18-N31.
9. Tao AT, Shu Y, Tan ET, et al. Improving apparent diffusion coefficient accuracy on a compact 3T MRI scanner using gradient nonlinearity correction. J Magn Reson Imaging 2018;48:1498-1507.
10. Foo TKF, Laskaris E, Vermilyea M, et al. Lightweight, compact, and high-performance 3T MR system for imaging the brain and extremities. Magn Reson Med 2018.
11. Foo TKF, Laskaris E, Vermilyea M, et al. Lightweight, compact, and high-performance 3T MR system for imaging the brain and extremities. Magn Reson Med 2018;80:2232-2245.
12. Foo TKF, Tan ET, Vermilyea ME, et al. Highly efficient head-only magnetic field insert gradient coil for achieving simultaneous high gradient amplitude and slew rate at 3.0T (MAGNUS) for brain microstructure imaging. Magn Reson Med 2020;83:2356-2369.
13. Yang GK, Tan ET, Fiveland E, Foo T, McNab JA. Measuring time-dependent diffusion kurtosis using the MAGNUS high-performance head gradient. In Proceedings of the 28th Annual Meeting of ISMRM, Virtual Meeting, 2020. Abstract 0962.
14. Andersson JLR, Skare S, Ashburner J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. NeuroImage 2003;20:870-888.
15. Andersson JLR, Sotiropoulos SN. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. NeuroImage 2016;125:1063-1078.
16. Ades-Aron B, Veraart J, Kochunov P, et al. Evaluation of the accuracy and precision of the diffusion parameter EStImation with Gibbs and NoisE removal pipeline. Neuroimage 2018;183:532-543.
17. Avants BB, Tustison N, Song G. Advanced normalization tools (ANTS). Insight j 2009;2:1-35.
18. Tan ET, Marinelli L, Slavens ZW, King KF, Hardy CJ. Improved correction for gradient nonlinearity effects in diffusion-weighted imaging. J Magn Reson Imaging 2013;38:448-453.
19. Fischl B. FreeSurfer. Neuroimage 2012;62:774-781.
20. Novikov DS, Jensen JH, Helpern JA, Fieremans E. Revealing mesoscopic structural universality with diffusion. Proc Natl Acad Sci U S A 2014;111:5088-5093.
21. Aggarwal M, Smith MD, Calabresi PA. Diffusion-time dependence of diffusional kurtosis in the mouse brain. Magn Reson Med 2020;84:1564-1578.
Figures

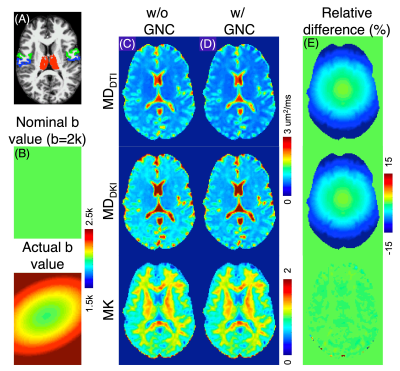
Figure 1. (A) Example GM ROIs (red: thalamus; green: precentral cortex; blue: postcentral cortex). (B) Example b value (nominal b=2000 s/mm2) with and without GNC. Diffusion measure maps (MDDTI, MDDKI, and MK) without and with GNC at f=0 are shown in (C) and (D), respectively. The relative MD (MK) difference maps (%) with and without GNC are displayed in (E).
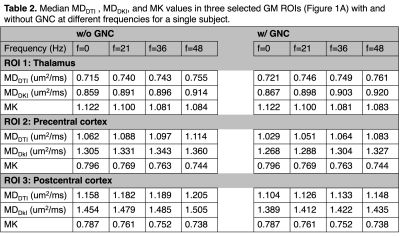
Table 2. Median MDDTI, MDDKI, and MK values in three selected GM ROIs (Figure 1A) with and without GNC at different frequencies for a single subject.
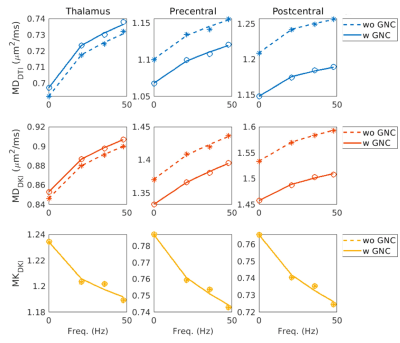
Figure 2. MD and MK measures (averaged across different subjects) and power-law fitting curves, with (solid lines and circles) and without (dashed lines and asterisks) GNC.
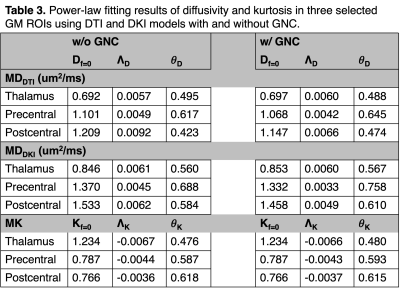
Table 3. Power-law fitting results of diffusivity and kurtosis in three selected GM ROIs using DTI and DKI models with and without GNC.