0684
Exchange between structurally-disordered compartments1Radiology, NYU School of Medicine, New York, NY, United States
Synopsis
Keywords: Microstructure, Modelling, exchange, diffusion, structural disorder
Which signatures of the diffusion signal are responsible for non-Gaussian diffusion inside cells or extra-cellular space, and which ones are the hallmark of the exchange between compartments? Answering this unresolved question is vital for mapping tissue microstructure in brain (especially in gray matter) and body. Here we employ the effective medium formalism to extend the multi-site exchange approach onto the case when diffusion in each tissue compartment is arbitrarily complex. We find the time-dependent diffusivity and kurtosis of a general system of exchanging non-Gaussian compartments for all times, validate with Monte Carlo simulations, and discuss practical implications.Introduction
Measuring water exchange has been a canonical NMR setup1–5, with recent applications in dMRI of tumors6–8 and in neuronal tissue9–16. The ion-channel component of transmembrane exchange10,11 enables mapping of metabolic activity in vivo. However, the widely ranging exchange time values in neurons, from a few ms to few hundred ms9,12,15–17, have stimulated an on-going discussion13,18 about the adequacy of the underlying site-exchange paradigm — based on coupled rate equations (the Karger model1, or KM) — for structurally complex tissues.The limitations of the KM are:
(i) The exchange must be barrier-limited, rather than diffusion-limited1,19;
(ii) KM is inapplicable for short diffusion times $$$t$$$, and only applies for sufficiently long $$$t$$$, when diffusion in each compartment becomes Gaussian19;
(iii) KM can become confounded by the slowly-decaying non-Gaussian effects, such as power-law tails in time-dependent diffusivity $$$D(t)$$$ and kurtosis $$$K(t)$$$, due to the structural disorder.20,21
Limitation (ii) is most pronounced for fully-confining cells (e.g., tumors), while limitation (iii) is especially relevant for recent dMRI measurements in gray matter13,15,16 in the cumulant regime, initiating the debate13,15,16,18 whether either exchange or structural disorder contributes most to time-dependent $$$D(t)$$$ and $$$K(t)$$$.
Here, under assumption (i), we offer an effective medium theory22 (EMT)-based extension of KM, that successfully resolves limitations (ii) and (iii) for any non-Gaussian compartments. Our theoretical expressions are validated with Monte-Carlo (MC) simulations of $$$D(t)$$$ and $$$K(t)$$$ in randomly-packed fiber geometry for all $$$t$$$, short and long, and provide for the first time an explicit interplay between the disorder-induced power-law tails and the site-exchange phenomena.
Theory
KM is a system of coupled rate equations $$\frac{\partial}{\partial t}\begin{pmatrix}m_1\\m_2\end{pmatrix}=-\left[\begin{pmatrix}D_1q^2&0\\0&D_2q^2\end{pmatrix}+\mathcal{R}\right]\begin{pmatrix}m_1\\m_2\end{pmatrix}+\begin{pmatrix}p_1\\p_2\end{pmatrix}\delta(t)\qquad(1)$$ where the elements of the rate matrix $$$\mathcal{R}=\begin{pmatrix}r_1&-r_2\\-r_1&r_2\end{pmatrix}$$$ are bound by the detailed-balance $$$p_1r_1=p_2r_2$$$, and compartment populations are normalized to $$$p_1+p_2=1$$$. The exchange rate $$r_\mathrm{ex}=r_1+r_2\equiv1/\tau_\mathrm{ex}$$ defines the mixing (exchange) time $$$\tau_\mathrm{ex}$$$.Known extensions5 of system (1) have assumed the lack of memory: the right-hand side does not contain information about system for times before $$$t$$$. Such framework is too restrictive to include effects of structural disorder13,20–22 that break the central limit theorem (CLT) and modify Fick’s law via a memory kernel22.
EMT+KM: Our idea is to represent any non-Gaussian diffusion in each compartment via the EMT form in the frequency representation, $$$\partial/\partial t\mapsto-i\omega$$$ and $$$\delta(t)\mapsto1$$$:
$$-i\omega\begin{pmatrix}m_1\\m_2\end{pmatrix}=-\left[\begin{pmatrix}D_1q^2-\Sigma_1(\omega,q)&0\\0&D_2q^2-\Sigma_2(\omega,q)\end{pmatrix}+\mathcal{R}\right]\begin{pmatrix}m_1\\m_2\end{pmatrix}+\begin{pmatrix}p_1\\p_2\end{pmatrix}\qquad(2)$$ where compartment signals have the EMT form (when $$$\mathcal{R}\equiv0$$$)
$$m_\alpha(\omega,q)=\frac{p_\alpha}{-i\omega+D_\alpha q^2-\Sigma_\alpha(\omega,q)}\,,\quad\alpha=1,2\,.\qquad(3)$$ The self-energy parts $$$\Sigma_\alpha(\omega,q)$$$ contain all non-Gaussian effects. Their Taylor expansions $$\Sigma_\alpha(\omega,q)=\Sigma_\alpha^{(2)}(\omega)q^2+\Sigma_\alpha^{(4)}(\omega)q^4+\dots\qquad(4)$$ define the dispersive (OGSE-measured) diffusivities $$$\mathcal{D}_\alpha(\omega)=D_\alpha-\Sigma_\alpha^{(2)}(\omega)$$$; the dispersive kinetic coefficients $$$\Sigma_\alpha^{(2),(4),\dots}(\omega)$$$ embrace the non-CLT (memory) effects (via convolutions in the time-domain), and yield time-dependent cumulants such as $$c^{(2)}_\alpha(t)=\langle x_\alpha^2(t)\rangle\equiv2tD_\alpha(t)\,,\quad c^{(4)}_\alpha(t)=\langle x_\alpha^4(t)\rangle-3\langle x_\alpha^2(t)\rangle^2,\quad\alpha=1,2\,,\qquad(5)$$ where $$$c^{(2)}_\alpha(t)$$$ is given by the Fourier integral that only involves $$$\Sigma_\alpha^{(2)}(\omega)$$$, and $$$c^{(4)}_\alpha(t)$$$ involves both $$$\Sigma_\alpha^{(2)}(\omega)$$$ and $$$\Sigma_\alpha^{(4)}(\omega)$$$, ref.22.
Exact solution of EMT+KM: The exchange matrix $$$\mathcal{R}$$$ mixes the compartments. The result of this mixing can be found algebraically and exactly for any $$$\Sigma_{1,2}(\omega,q)$$$ from Eq.(2) without solving any differential equations. The overall signal $$S(\omega,q)=m_1+m_2\equiv\frac1{-i\omega+\overline{D}q^2-\Sigma(\omega,q)}\qquad(6)$$ can be represented in the EMT form (3), where $$$\overline{D}=p_1D_1+p_2D_2$$$ and $$\Sigma(\omega,q)=\overline{\Sigma}(\omega,q)+\frac{p_1p_2[D_1q^2-D_2q^2-\Sigma_1(\omega,q)+\Sigma_2(\omega,q)]^2}{-i\omega+(D_1+D_2-\overline{D})q^2-[\Sigma_1(\omega,q)+\Sigma_2(\omega,q)-\overline{\Sigma}(\omega,q)]+r_\mathrm{ex}}\,,\qquad(7)$$ where $$$\overline{\Sigma}(\omega,q)=p_1\Sigma_1(\omega,q)+p_2\Sigma_2(\omega,q)$$$.
Note that we have not specified anything about diffusion in either compartment. The only barrier-limited diffusion assumption (i) ensures that the compartments are well-defined, such that EMT signal form in one compartment is not destroyed by the exchange with another.
Using expansion (4) up to $$$O(q^2)$$$, we find that the overall diffusivity $$\mathcal{D}(\omega)=p_1\mathcal{D}_1(\omega)+p_2\mathcal{D}_2(\omega)\qquad(8)$$ is weighted-average, independent of exchange $$$r_\mathrm{ex}$$$, extending this KM property onto time-dependent diffusivities: $$D(t)=p_1D_1(t)+p_2D_2(t)\,.\qquad(9)$$
Kurtosis requires expansion up to $$$O(q^4)$$$; the corresponding overall 4th-order term $$\Sigma^{(4)}(\omega)=p_1\Sigma_1^{(4)}(\omega)+p_2\Sigma_2^{(4)}(\omega)+\frac{p_1p_2[\mathcal{D}_1(\omega)-\mathcal{D}_2(\omega)]^2}{-i\omega+r_\mathrm{ex}}$$ in combination with the overall $$$\mathcal{D}(\omega)$$$ yields $$$K(t)=c^{(4)}(t)/[2tD(t)]^2$$$, where the overall 4th-order cumulant $$c^{(4)}(t)=c^{(4)}_{r_\mathrm{ex}=0}(t)+\delta c^{(4)}_{r_\mathrm{ex}}(t)\,,\qquad(10)$$ and $$c^{(4)}_{r=0}(t)=p_1c^{(4)}_1(t)+p_2c^{(4)}_2(t)+12t^2 p_1p_2[D_1(t)-D_2(t)]^2\qquad(11)$$is the exact 4th-order cumulant without exchange. The nontrivial result is the exchange contribution $$\delta c^{(4)}_{r_\mathrm{ex}}(t)=-4!\cdot r_\mathrm{ex}\,p_1p_2\left[f(t)-r_\mathrm{ex}\int_0^t\!d\tau\,e^{-r_\mathrm{ex}(t-\tau)}f(\tau)\right]\leq0\,,\qquad(12)$$ where $$f(t)=\frac14\int_0^t\!d\tau\,\Delta c^{(2)}(t-\tau)\Delta c^{(2)}(\tau)\,,\quad\Delta c^{(2)}(t)=c^{(2)}_1(t)-c^{(2)}_2(t)=2t[D_1(t)-D_2(t)]\,.\qquad(13)$$
For Gaussian compartments, $$$c^{(4)}_{1,2}\equiv0$$$, and $$$\Delta\,c^{(2)}(t)=2(D_1-D_2)t$$$ yields $$c^{(4)}_\mathrm{KM}(t)=4!\cdot p_1p_2(D_1-D_2)^2\,\frac{e^{-r_\mathrm{ex}t}-1+r_\mathrm{ex}t}{r_\mathrm{ex}^2}\qquad(14)$$ corresponding to KM kurtosis19 $$$K_\mathrm{KM}(t)=c^{(4)}_\mathrm{KM}(t)/(2\overline{D}t)^2$$$.
Structural disorder contributes to non-exchanging component $$$c^{(4)}_{r_\mathrm{ex}=0}(t)$$$ via nontrivial $$$c^{(4)}_\alpha(t)$$$ and $$$[D_1(t)-D_2(t)]^2$$$ in Eq.(11). Equation (12) provides the desired interplay between exchange and structural disorder contributing to overall kurtosis.
Validation
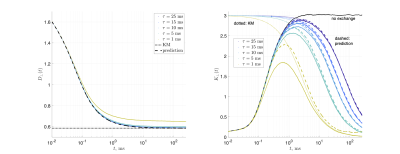
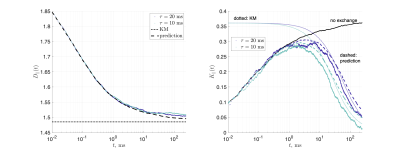
Substrates: Two geometries of randomly packed parallel cylinders were generated with fraction $$$p_1=0.5$$$ and diameter $$$a=$$$1μm (Fig.1). The 2d substrate had 14325 cylinders, and size $$$150\times150$$$μm2. The 3d substrate had 673 cylinders and size 32.5×32.5×32.5μm3; 30 barriers were placed randomly inside each cylinder, with average separation of $$$\bar a=1.084$$$μm.MC simulations were performed in RMS28 with 106 spins, $$$D_0=D(t)|_{t=0}=$$$2ms/μm2, and $$$t\leq\,250$$$ms. For 2d, $$$dt=10^{-4}$$$ms. Simulations were performed on each compartment separately, and then with permeable membranes such that $$$\tau_\mathrm{ex}=a/2\kappa=1,5,10,15,25$$$ms, resulting in $$$D_\perp(t)$$$ and $$$K_\perp(t)$$$.
For the 3d geometry, $$$dt=2\cdot10^{-4}$$$ms and $$$\tau_\mathrm{ex}=10, 20$$$ms, yielding $$$D_\parallel(t)$$$ and $$$K_\parallel(t)$$$ along cylinders. Permeability $$$\kappa_\mathrm{in}$$$ for the barriers inside the cylinders corresponded to a strength of restrictions $$$\zeta=D_0/\kappa_\mathrm{in}\bar a=1$$$, such that $$$D_{\infty,1}=D_0/(1+\zeta)$$$ and $$$D_{\infty,2}=D_0$$$.
Results and Discussion
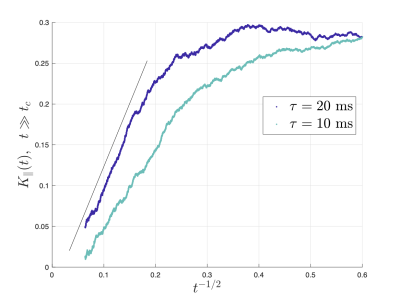
Figs.2,3 show the predicted $$$D(t)$$$ and $$$K(t)$$$, based on non-exchanging simulated compartmental cumulants $$$c^{(2)}_\alpha(t)$$$ and $$$c^{(4)}_\alpha(t)$$$. Accuracy in Fig.2 reaches a few percent when exchange becomes barrier-limited.The power-law tails13 in overall $$c^{(4)}(t)=p_1c^{(4)}_1(t)+p_2c^{(4)}_2(t)+c^{(4)}_\mathrm{KM}(t)-4!\cdot p_1p_2(D_{\infty,1}-D_{\infty,2})\left(\frac{\vartheta_1A_1t^{2-\vartheta_1}}{(2-\vartheta_1)(1-\vartheta_1)}-\frac{\vartheta_2A_2t^{2-\vartheta_2}}{(2-\vartheta_2)(1-\vartheta_2)}\right)+\dots\qquad(15)$$ decay slower than KM kurtosis for $$$\vartheta_\alpha\leq1$$$ (Fig.4).
Conclusions and Outlook
EMT+KM is a model-independent framework to “mix” compartments with arbitrarily complex diffusion. It enables assembling the signal from “building blocks” based on compartment models,13,20,21,23 MC simulations,24–28 or perhaps even rescaled measurements of compartment-specific metabolites.24,29,30Acknowledgements
We thank Hong-Hsi Lee for useful discussions. This work was supported by NIH under NINDS award R01 NS088040 and NIBIB awards R01 EB027075, and was performed under the rubric of the Center for Advanced Imaging Innovation and Research (CAI2R, https://www. cai2r.net), a NIBIB Biomedical Technology Resource Center (NIH P41- EB017183).References
1 Jorg Karger, “NMR self-diffusion studies in heterogeneous systems,” Advances in Colloid and Interface Science 23, 129–148 (1985).
2 P W Kuchel, A Coy, and P Stilbs, “NMR ”diffusion-diffraction” of water revealing alignment of erythrocytes in a magnetic field and their dimensions and membrane transport characteristics.” Magnenetic Resonance in Medicine 37, 637–643 (1997).
3 Christian Meier, Wolfgang Dreher, and Dieter Leibfritz, “Diffusion in compartmental systems. I. A comparison of an analytical model with simulations,” Magnetic Resonance in Medicine 50, 500–509 (2003).
4 Ingrid Aslund, Agnieszka Nowacka, Markus Nilsson, and Daniel Topgaard, “Filter-exchange PGSE NMR determination of cell membrane permeability,” J. Magn. Reson. 200, 291–295 (2009).
5 Nicolas Moutal, Markus Nilsson, Daniel Topgaard, and Denis Grebenkov, “The Karger vs bi-exponential model: Theoretical insights and experimental validations,” Journal of Magnetic Resonance 296, 72–78 (2018).
6 Olivier Reynaud, “Time-Dependent Diffusion MRI in Cancer: Tissue Modeling and Applications,” Frontiers in Physics 5, 1–16 (2017).
7 Xiaoyu Jiang, Hua Li, Jingping Xie, Eliot T Mckinley, Ping Zhao, John C Gore, and Junzhong Xu, “In Vivo Imaging of Cancer Cell Size and Cellularity Using Temporal Diffusion Spectroscopy,” Magnenetic Resonance in Medicine 164, 156–164 (2017).
8 Junzhong Xu, Xiaoyu Jiang, Hua Li, Lori R. Arlinghaus, Eliot T. McKinley, Sean P. Devan, Benjamin M. Hardy, Jingping Xie, Hakmook Kang, A. Bapsi Chakravarthy, and John C. Gore, “Magnetic resonance imaging of mean cell size in human breast tumors,” Magnetic Resonance in Medicine 83, 2002–2014 (2020), 1905.07818.
9 Markus Nilsson, Jimmy Latt, Danielle Van Westen, Sara Brockstedt, Samo Lasic, Freddy Stahlberg, and Daniel Topgaard, “Noninvasive mapping of water diffusional exchange in the human brain using filter-exchange imaging,” Magnetic Resonance in Medicine 69, 1573–1581 (2013).
10 Ruiliang Bai, Charles S. Springer, Dietmar Plenz, and Peter J. Basser, “Fast, Na+/K+ pump driven, steady-state transcytolemmal water exchange in neuronal tissue: A study of rat brain cortical cultures,” Magnetic Resonance in Medicine 79, 3207–3217 (2018).
11 Ruiliang Bai, Zhaoqing Li, Chaoliang Sun, Yi Cheng Hsu, Hui Liang, and Peter Basser, “Feasibility of filter-exchange imaging (FEXI) in measuring different exchange processes in human brain,” NeuroImage 219, 117039 (2020).
12 Nathan H. Williamson, Rea Ravin, Dan Benjamini, Hellmut Merkle, Melanie Falgairolle, Michael J. O’donovan, Dvir Blivis, Dave Ide, Teddy X. Cai, Nima S. Ghorashi, Ruiliang Bai, and Peter J. Basser, “Magnetic resonance measurements of cellular and sub-cellular membrane structures in live and fixed neural tissue,” eLife 8 (2019), 10.7554/eLife.51101.
13 Hong-Hsi Lee, Antonios Papaioannou, Dmitry S. Novikov, and Els Fieremans, “In vivo observation and biophysical interpretation of time-dependent diffusion in human cortical gray matter,” NeuroImage 222, 117054 (2020).
14 Nathan H. Williamson, Rea Ravin, Teddy X. Cai, Dan Benjamini, Melanie Falgairolle, Michael J. O’Donovan, and Peter J. Basser, “Real- time measurement of diffusion exchange rate in biological tissue,” Journal of Magnetic Resonance 317, 106782 (2020).
15 Ileana O. Jelescu, Alexandre de Skowronski, Franc ̧oise Geffroy, Marco Palombo, and Dmitry S. Novikov, “Neurite Exchange Imaging (NEXI): A minimal model of diffusion in gray matter with inter-compartment water exchange,” NeuroImage 256, 119277 (2022).
16 Jonas L. Olesen, Leif Ostergaard, Noam Shemesh, and Sune N. Jespersen, “Diffusion time dependence, power-law scaling, and exchange in gray matter,” NeuroImage 251, 118976 (2022).
17 Donghan M. Yang, James E. Huettner, G. Larry Bretthorst, Jeffrey J. Neil, Joel R. Garbow, and Joseph J.H. Ackerman, “Intracellular water preexchange lifetime in neurons and astrocytes,” Magnetic Resonance in Medicine 79, 1616–1627 (2018).
18 Mohammad Khateri, Marco Reisert, Alejandra Sierra, Jussi Tohka, and Valerij G. Kiselev, “What does FEXI measure?” NMR in Biomedicine (2022), 10.1002/nbm.4804.
19 E Fieremans, Dmitry S Novikov, J H Jensen, and J A Helpern, “Monte Carlo study of a two-compartment exchange model of diffusion,” NMR in Biomedicine 23, 711–724 (2010).
20 Dmitry S Novikov, Jens H Jensen, Joseph A Helpern, and Els Fieremans, “Revealing mesoscopic structural universality with diffusion.” Proceedings of the National Academy of Sciences of the United States of America 111, 5088–93 (2014).
21 Lauren M Burcaw, Els Fieremans, and Dmitry S Novikov, “Mesoscopic structure of neuronal tracts from time-dependent diffusion,” NeuroImage 114, 18–37 (2015).
22 Dmitry S. Novikov and Valerij G Kiselev, “Effective medium theory of a diffusion-weighted signal,” NMR Biomed 23, 682–697 (2010).
23 Paul T Callaghan, “Pulsed-gradient spin-echo nmr for planar, cylindrical, and spherical pores under conditions of wall relaxation,” Journal of Magnetic Resonance, Series A 113, 53–59 (1995).
24 Marco Palombo, Cle ́mence Ligneul, Chloe ́ Najac, Juliette Le Douce, Julien Flament, Carole Escartin, Philippe Hantraye, Emmanuel Brouil- let, Gilles Bonvento, and Julien Valette, “New paradigm to assess brain cell morphology by diffusion-weighted MR spectroscopy in vivo,” Proceedings of the National Academy of Sciences 113, 201504327 (2016).
25 Marco Palombo, Clemence Ligneul, Edwin Hernandez-Garzon, and Julien Valette, “Can we detect the effect of spines and leaflets on the diffusion of brain intracellular metabolites?” NeuroImage 182, 283–293 (2018).
26 Kevin Ginsburger, Fabrice Poupon, Justine Beaujoin, Delphine Estournet, Felix Matuschke, Jean-Franc ̧ois Mangin, Markus Axer, and Cyril Poupon, “Improving the Realism of White Matter Numerical Phantoms: A Step toward a Better Understanding of the Influence of Structural Disorders in Diffusion MRI,” Frontiers in Physics 6, 12 (2018).
27 Hong Hsi Lee, Antonios Papaioannou, Sung Lyoung Kim, Dmitry S. Novikov, and Els Fieremans, “A time-dependent diffusion MRI signature of axon caliber variations and beading,” Communications Biology 3, 354 (2020).
28 Hong-Hsi Lee, Els Fieremans, and Dmitry S Novikov, “Realistic Microstructure Simulator (RMS): Monte Carlo simulations of diffusion in three-dimensional cell segmentations of microscopy images,” Journal of Neuroscience Methods (2020).
29 Joseph J H Ackerman and Jeffrey J Neil, “The use of MR-detectable reporter molecules and ions to evaluate diffusion in normal and ischemic brain,” NMR Biomed 23, 725–733 (2010).
30 Cle ́mence Ligneul, Marco Palombo, Edwin Herna ́ndez-Garzo ́n, Mar ́ıa Angeles Carrillo-de Sauvage, Julien Flament, Philippe Hantraye, Emmanuel Brouillet, Gilles Bonvento, Carole Escartin, and Julien Valette, “Diffusion-weighted magnetic resonance spectroscopy enables cell-specific monitoring of astrocyte reactivity in vivo,” NeuroImage 191, 457–469 (2019).
Figures