0681
Localization Regime of Diffusion (LoRD) in mouse and pig cortical gray matter and its sensitivity to soma size
Hong-Hsi Lee1,2, Nian Wang3,4, Els Fieremans5, Susie Y Huang1,2, and Dmitry S Novikov5
1Radiology, Athinoula A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Charlestown, MA, United States, 2Radiology, Harvard Medical School, Boston, MA, United States, 3Radiology and Imaging Sciences, Indiana University School of Medicine, Indianapolis, IN, United States, 4Stark Neurosciences Research Institute, Indianapolis, IN, United States, 5Center for Advanced Imaging Innovation and Research, New York University School of Medicine, New York, NY, United States
1Radiology, Athinoula A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Charlestown, MA, United States, 2Radiology, Harvard Medical School, Boston, MA, United States, 3Radiology and Imaging Sciences, Indiana University School of Medicine, Indianapolis, IN, United States, 4Stark Neurosciences Research Institute, Indianapolis, IN, United States, 5Center for Advanced Imaging Innovation and Research, New York University School of Medicine, New York, NY, United States
Synopsis
Keywords: Microstructure, Gray Matter
It is non-trivial to decompose the diffusion MRI signal, as conventionally measured using relatively weak gradients, into contributions from multiple compartments and estimate the cell sizes. Instead, using strong diffusion gradients, a universal compartment-independent localization regime emerges, as they saturate all magnetization except that near cell membranes. The signal sensitivity to the membrane and its surface-to-volume ratio enables the soma size estimation without modeling multiple compartments. Here, we observed the unique functional form of localization regime and estimate the soma size in mouse and pig brains cortical gray matter on a Bruker CryoProbe system.Introduction
Cell size estimation using diffusion MRI requires biophysical modeling of multiple compartments, such as intra- and extra-cellular spaces, whose signals are described by cumulant expansion using relatively low gradients or b-values [1]. However, it is non-trivial to decompose signal contributions from each compartment due to limited amount of data and the degeneracy of models in this regime [2]. Instead, at high diffusion gradients $$$G$$$ (Larmor gradient $$$g=\gamma G$$$), the cumulant expansion is invalid, and a universal compartment-independent localization regime emerges [3,4]: The strong diffusion gradient saturates all magnetization except that near cell walls, within a thickness of localization length $$$l_g\propto g^{-1/3}$$$ . This signal sensitivity to the membrane and its surface-to-volume ratio provides sensitivity to soma size. Here, we observe the localization regime of diffusion and estimate the soma size in the cortical gray matter (GM) on a Bruker scanner using strong gradients $$$G$$$ up to 660 mT/m in mouse (ex vivo/in vivo) and pig (ex vivo) brains.Theory
In the localization regime, the dMRI signal measured by applying strong gradients decays as $$$-\ln S\sim(bD_0)^{1/3}\propto g^{2/3}$$$, where $$$D_0$$$ is the intrinsic diffusivity. Due to strong gradients, magnetization far from the membranes vanishes, and only spins within a layer of $$$l_g\equiv(D_0/g)^{1/3}$$$ close to the membrane contribute to the signal (Fig. 1a) [3]. The localization regime emerges when the localization length is smaller than both the cell size and the diffusion length $$$l_\delta=\sqrt{D_0\delta}$$$ , where the pulse width $$$\delta\propto\Delta$$$ is comparable to diffusion time in a pulsed-gradient sequence. For diffusion in a medium of spheres with radius $$$R$$$, the dMRI signal $$$S$$$ in localization regime is given by [3,4]$$S/S_0\simeq(1-f_\text{im})\cdot\frac{S_++S_-}{2}+f_\text{im}\,,$$
where $$$f_\text{im}$$$ is the signal fraction of immobile water (ex vivo scan) or the noise floor (in vivo scan), and $$$S_\pm$$$ are signals inside and outside spheres [4,5]:
$$S_\pm(g,\delta)\simeq C_\pm\left(\frac{l_g}{R}\right)^{5/2}\cdot\exp\left(-a_1\frac{l_\delta^2}{l_g^2}-2\frac{l_\delta^2}{R^{1/2}l_g^{3/2}}\pm\sqrt{3}\frac{l_\delta^2}{a_1Rl_g}\right)$$
with $$$a_1$$$=1.02, and constants $$$C_\pm$$$ related to the diffusion eigenmodes. Empirically, $$$C_+\approx13$$$ is estimated based on diffusion simulations in spheres (Fig. 1b) [5]. For simplicity, we take $$$C_-=C_+$$$ to estimate the soma radius $$$R$$$.
Methods
MRIAnimal experiments were carried out in compliance with the local Institutional Animal Care and Use Committee. Two wild-type adult C57BL/6 mice (Jackson Laboratory, Bar Harbor, ME) were chosen for dMRI imaging: one for ex vivo scans and another for in vivo scans. In addition, we performed ex vivo dMRI in a pig brain. MR images of mouse and pig brains were acquired on a 30-cm bore 9.4T magnet (Bruker BioSpec 94/30, Billerica, MA). A high-sensitivity cryogenic RF surface receive-only coil was used for signal reception (Bruker CryoProbe). Other parameters are given below:
Ex vivo MRI (mouse) 3D-EPI, room temperature, (200 µm)3 voxel size, pulse duration = 12 ms, pulse separation = 17 ms, TE = 35.5 ms, TR = 208 ms, 6 b=0 images + 15 b-values = 1-50 ms/µm2, 46 directions/b-shell.
In vivo MRI (mouse) 2D-EPI, 37˚C, 400 x 400 x 1600 µm3 voxel size, pulse duration = 5.6 ms, pulse seperation = 14 ms, TE = 25 ms, TR = 1500 ms, 8 b=0 images + 11 b-values = 0.5-10 ms/µm2, 28 directions/b-shell.
Ex vivo MRI (pig) 3D-EPI, room temperature, (600 μm)3 voxel size, pulse duration = 12 ms, pulse separation = 17 ms, TE = 36.8 ms, TR = 208 ms, 6 b=0 images + 15 b-values = 1-50 ms/µm2, 17 directions/b-shell.
Model fitting
Diffusion-weighted-images (DWIs) were averaged over directions for each b-shell (spherical mean signal). We fitted the above signal model of the localization regime to the spherical mean signal of $$$G$$$ > 400 mT/m in a cortical gray matter ROI. The intrinsic diffusivity $$$D_0$$$, soma radius $$$R$$$, and immobile water fraction $$$f_\text{im}$$$ were the fitted parameters for the ex vivo scan. The noise floor fraction $$$f_\text{im}$$$ was fixed at the value $$$\sigma_n/S_0$$$ for the in vivo scan, where $$$\sigma_n$$$ was the noise level in the ROI, estimated by MPPCA denoising [6].
Results
In the cortical GM ROI, the signal is consistent with the functional form of localization regime, especially when $$$G$$$ > 300 mT/m (Figs. 2 and 3). In the ex vivo scan, the signal roughly scales as $$$-\ln(S/S_0-f_\text{im})\sim b^{1/3}$$$ at high $$$b$$$ after subtracting the immobile water fraction (Figs. 2a and 3 inset), revealing the unique functional form of signal decay in the localization regime. The estimated soma radius is 3.9 µm (ex vivo mouse), 5.1 µm (in vivo mouse), and 4.1 μm (ex vivo pig), and the estimated intrinsic diffusivity is 0.8 µm2/ms (ex vivo mouse), 2.4 µm2/ms (in vivo mouse), and 1.4 μm2/ms (ex vivo pig), consistent with values in previous studies [7-9].Discussion and Conclusions
We demonstrated the localization regime of diffusion at strong gradients via in vivo (mouse) and ex vivo (mouse, pig) dMRI in cortical brain gray matter. At strong gradients $$$G$$$ > 300 mT/m, localization length $$$l_g$$$ < 2.2 µm (ex vivo mouse), < 3.1 µm (in vivo mouse), and < 2.6 μm (ex vivo pig) is smaller (although not by a lot) than the estimated soma size and diffusion length, satisfying the conditions for localization regime onset. In conclusion, dMRI measurements in the localization regime using strong gradients enable estimation of soma size without the need of modeling multiple compartments.Acknowledgements
This study is support by NIH under the award number: DP5OD031854, R01NS125020, P41EB015896, P41EB030006, U01EB026996, R01NS118187, R21NS081230, R01NS088040, P41EB017183.References
- Kiselev, V. G. (2010). The cumulant expansion: an overarching mathematical framework for understanding diffusion NMR. Diffusion MRI, 152-168.
- Jelescu, I. O., Veraart, J., Fieremans, E., & Novikov, D. S. (2016). Degeneracy in model parameter estimation for multi‐compartmental diffusion in neuronal tissue. NMR in Biomedicine, 29(1), 33-47.
- Stoller, S. D., Happer, W., & Dyson, F. J. (1991). Transverse spin relaxation in inhomogeneous magnetic fields. Physical Review A, 44(11), 7459.
- Moutal, N., Demberg, K., Grebenkov, D. S., & Kuder, T. A. (2019). Localization regime in diffusion NMR: theory and experiments. Journal of Magnetic Resonance, 305, 162-174.
- Lee et al., ISMRM 2021, 29, 0639.
- Veraart, J., Novikov, D. S., Christiaens, D., Ades-Aron, B., Sijbers, J., & Fieremans, E. (2016). Denoising of diffusion MRI using random matrix theory. Neuroimage, 142, 394-406.
- Dhital, B., Reisert, M., Kellner, E., & Kiselev, V. G. (2019). Intra-axonal diffusivity in brain white matter. NeuroImage, 189, 543-550.
- Zhang, J., Jones, M. V., McMahon, M. T., Mori, S., & Calabresi, P. A. (2012). In vivo and ex vivo diffusion tensor imaging of cuprizone‐induced demyelination in the mouse corpus callosum. Magnetic resonance in medicine, 67(3), 750-759.
- http://neuromorpho.org
Figures
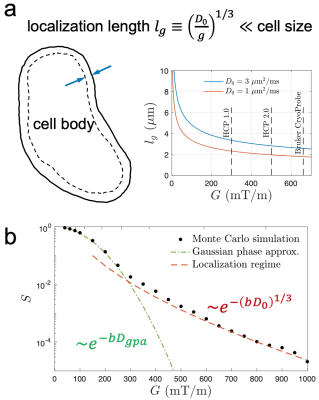
Fig. 1. (a) At high diffusion gradient G (Larmor gradient g=γG), all magnetization saturates except that near cell membranes within a thickness of localization length lg ~g -1/3. On a Bruker scanner with CryoProbe, localization length is 2-3 μm in biological tissues at G=660 mT/m. (b) The signal decay in localization regime (red) is much slower than that of Gaussian phase approximation (green).
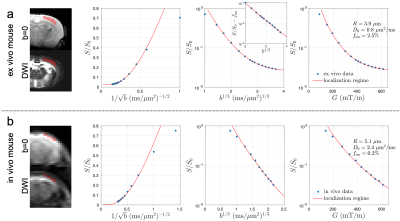
Fig. 2. In the mouse brain cortical GM ROI, the dMRI signal is consistent with the functional form of localization regime at G > 300 mT/m. (a) In the ex vivo scan, the signal scales as ~exp[-(bD0)1/3] at high b after subtracting the immobile water fraction (inset), indicating the unique functional form of localization regime. (a-b) The estimated soma radius and intrinsic diffusivity based on localization regime in mouse brains are consistent with values in previous studies [7-9].
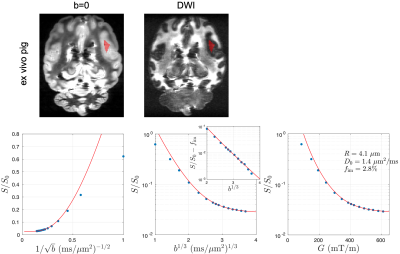
Fig. 3. In the pig brain cortical GM ROI, the dMRI signal is consistent with the functional form of localization regime at G > 300 mT/m. In the ex vivo scan, the signal scales as ~exp[-(bD0)1/3] at high b after subtracting the immobile water fraction (inset), indicating the unique functional form of localization regime. The estimated soma radius and intrinsic diffusivity based on localization regime in pig brain are consistent with values in previous studies [7-9].
DOI: https://doi.org/10.58530/2023/0681