0671
Improved T1 and T2 mapping in 3D-QALAS using temporal subspaces and Cramer-Rao-bound flip angle optimization enabled by auto-differentiation1Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA, United States, 2Department of Radiology, Martinos Center for Biomedical Imaging, Charlestown, MA, United States, 3Department of Radiology, Harvard Medical School, Boston, MA, United States, 4Department of Radiology, Boston Children's Hospital, Boston, MA, United States, 5Harvard-MIT Health Sciences and Technology, Massachusetts Institute of Technology, Cambridge, MA, United States, 6Institute for Medical Engineering and Science, Massachusetts Institute of Technology, Cambridge, MA, United States
Synopsis
Keywords: Quantitative Imaging, Pulse Sequence Design
3D-QALAS utilizes an interleaved Look-Locker acquisition with T2-preparation pulses for full brain quantification of T1 and T2. The sequence applies constant flip-angles and suffers from blurring due to k-space modulation from signal evolution during the lengthy echo-train. This abstract improves 3D-QALAS by (1) resolving the full temporal signal with subspace reconstructions to eliminate blurring, (2) optimizing acquisition flip angles with the Cramer-Rao-Bound using simulations compatible with auto-differentiation, and (3) decreasing the number of acquisitions within a repetition time, which could enable up to 40% reduced scan time. Simulation, phantom, and in-vivo results demonstrate the efficacy of the proposed sequence improvements.Introduction
T2 and T1 estimation improves characterization of various pathologies [1-6], but lengthy scan-times preclude widespread application of quantitative MRI (qMRI), so sequences have been developed for efficient 3D acquisitions [7–9]. For example, 3D-QALAS [10,11] utilizes an interleaved Look-Locker acquisition with a T2-preparation pulse for full brain quantification of T1 and T2. However, 3D-QALAS applies constant flip angles and reconstructs images at 5 time-points that suffer from blurring due to signal evolution during the acquisition echo-train.We propose improving quantitative mapping with 3D-QALAS by:
- Incorporating subspace-based reconstruction that resolves complete temporal dynamics to eliminate blurring.
- Optimizing acquisition flip angles with the Cramer-Rao-Bound (CRB) using signal simulation code compatible with auto-differentiation.
- Decreasing the number of total acquisitions per repetition time (TR) for reduced scan-time.
Methods
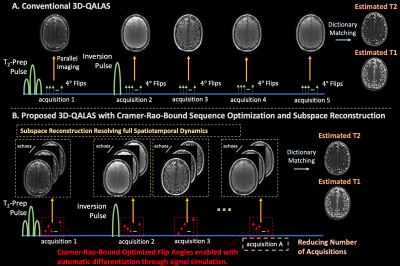
Figure 1(A) displays the conventional 3D-QALAS sequence with T2-prep, inversion, and 5 acquisitions which each utilize an echo-train of 4-degree flips. Parallel imaging reconstructs a 3D-volume for each acquisition, and a matching procedure [12] compares the 5 volumes to a pre-computed dictionary to estimate T1 and T2 maps. However, the flip-angle-trains are heuristically chosen for quantitative mapping, and signal evolution during the echo-trains modulates k-space, resulting in blurring and reduced model accuracy [13,14].Figure 1(B) and the text below describes our proposed improvements.
(1) Subspace Reconstruction: Let $$$E$$$ be the number of echoes in one of the $$$A$$$ acquisitions in a 3D-QALAS TR (typically $$$A = 5$$$, $$$E \approx 120 \rightarrow 120 \times 5 \approx 600$$$ echoes/TR). Rather than reconstructing 5 volumes with k-space aggregation, let $$$x \in \mathbb{C}^{M \times N \times P \times T}$$$ be volumes at each echo, where $$$T=A \times E$$$. Subspace techniques simulate a dictionary of signal evolution and generate a singular-value-decomposition derived linear basis, $$$\Phi \in \mathbb{C}^{T \times B}$$$, to produce a traceable reconstruction problem:
$$argmin_{\alpha} ||y - A \Phi \alpha|| + R(\alpha)$$
where $$$A$$$ represents the Fourier, coil, and sampling operators, and $$$\alpha \in \mathbb{C}^{M \times N \times P \times B}$$$ represents the low-dimensional subspace coefficients ($$$B << T$$$). To estimate quantitative maps, we set $$$x = \Phi \alpha$$$ and utilize dictionary matching with $$$T$$$ echoes. By resolving full spatial temporal dynamics, we aim to reconstruct sharper quantitative maps [13,15].
(2) CRB Flip-Angle Optimization: Previous work uses the CRB, the minimum achievable variance of an unbiased estimator, for sequence optimization [16,17]. Let $$$CRB(\theta,FA)$$$ represent the CRB of 3D-QALAS for parameters $$$\theta=[T_2, T_1, M_0]$$$ and flip angles $$$FA$$$. We implemented auto-differentiation compatible signal simulation [17] for 3D-QALAS, enabling computation of gradients to $$$minimize_{FA} CRB(\theta,FA)$$$, yielding optimized flip angles for parameter estimation.
(3) We designed flip angles for 3D-QALAS sequences with a reduced number of acquisitions, thereby reducing the TR to enable faster mapping with similar accuracy.
Experiments
All experiments Fourier transformed the fully-sampled read-out dimension to analyze a single slice and utilized BART [18] for subspace reconstructions.Conventional vs. Subspace: We acquired conventional 3D-QALAS data in-vivo with 1.23x1.23x1.23 mm3 resolution and compared T2 and T1 estimates with conventional and proposed subspace (B=3) reconstructions.
Flip-Angle Optimization: Next, we optimized the flip angles in 3D-QALAS by minimizing CRB with auto-differentiation in two regimes: (1) optimizing one flip angle per echo-train (2) optimizing all flip angles in every echo-train. We initialized both optimizations with the conventional 4-degree flip angles, utilized representative tissue parameters $$$\theta^1=[T_2=70ms,T_1=700ms,M_0=1]$$$ and $$$\theta^2=[T_2=80ms,T_1=1300ms,M_0=1]$$$, and minimized the CRB-based cost function with the ADAM [19] optimizer in Pytorch. Finally, we designed optimized sequences with $$$A={5,4,3}$$$ acquisitions by removing acquisitions from the end of the TR, thus reducing scan time.
Simulation Experiments: Using T1, T2, and M0 estimates from the aforementioned in-vivo dataset, we simulated multi-channel 3D-QALAS k-space (with added noise) using constant, optimized per echo-train, and all optimized flip angles with $$$A={3,4,5}$$$ acquisitions. Quantitative maps were estimated with subspace reconstructions ($$$B=3$$$) and dictionary matching.
Phantom and In-vivo Experiment: We implemented the optimized-per-echo-train 3D-QALAS sequence on the scanner and acquired data using the conventional constant and optimized flip angle sequences on the Mini System Phantom, Model #136 (CaliberMRI, Boulder, CO, USA) and a human subject (under IRB approval) with 3 and 5 acquisitions (1x1x1 mm3 resolution, R=2). We compared quantitative maps estimated with subspace reconstructions and dictionary matching ($$$B=3$$$).
Results
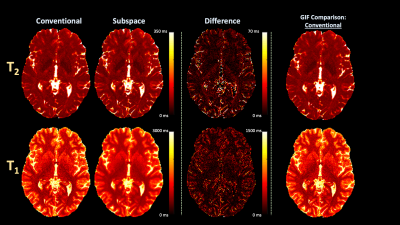
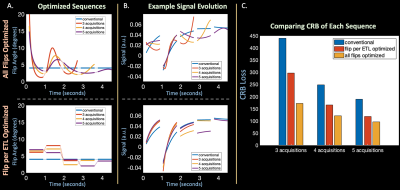
Figure 2 (A) and (B) compares estimated quantitative maps from in-vivo data with and without subspace reconstruction and (C) toggles between the two demonstrating reduced blurring in T2 and noise in T1 using subspaces.Figure 3 (A) plots optimized flip angles, (B) corresponding signal evolution, and (C) resultant CRB, where optimized flip angles improve or match conventional CRB based on acquisition number.
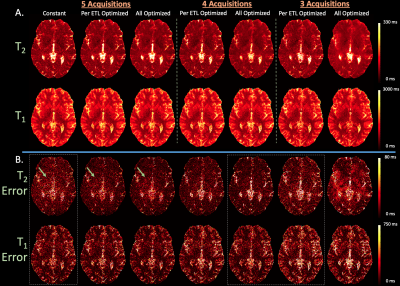
Figure 4 (A) and (B) compares reconstructed maps and corresponding errors from simulated data where the optimized sequences with 5 acquisitions achieves best estimation, while optimized sequences with fewer acquisitions match the conventional sequence with 5 acquisitions.
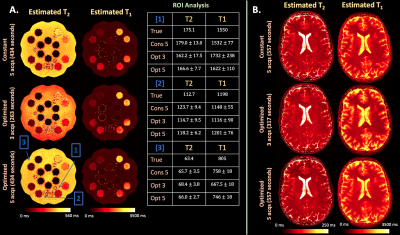
Figure 5 (A) and (B) display estimated maps from phantom and in-vivo data where the per-ETL-flip-angle-optimized sequences with $$$A=3,5$$$ acquisitions matches constant flip angle parameter estimation.
Example Code: https://anonymous.4open.science/r/ismrm2023_qalas_optimized-13C8/
Conclusion
Future work will implement the all-flip-angle-optimized sequence to address some of the T1-bias in the prospective experiments. Combining subspace reconstruction with auto-differentiation enabled flip-angle optimization yields improved 3D-QALAS sequences with up to 40% reduced scan-time and sharper quantitative maps.Acknowledgements
This work was supported in part by research grants NIH R01 EB032708, R01HD100009, R01 EB028797, U01 EB025162, P41 EB030006, U01 EB026996, R03EB031175, R01EB032378 and the NVidia Corporation for computing support. This research was also supported by the National Institute of Biomedical Imaging and Bioengineering (NIBIB), of the National Institutes of Health under award number 5T32EB1680. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.References
[1] MacKay, A. L. et al. MR relaxation in multiple sclerosis. Neuroimaging Clin. N. Am. 19, 1–26 (2009).
[2] Liao, C. et al. Detection of Lesions in Mesial Temporal Lobe Epilepsy by Using MR Fingerprinting. Radiology 288, 804–812 (2018).
[3] Ma, D. et al. Development of high-resolution 3D MR fingerprinting for detection and characterization of epileptic lesions. J. Magn. Reson. Imaging 49, 1333–1346 (2019).
[4] Stevenson, V. L. et al. Variations in T1 and T2 relaxation times of normal appearing white matter and lesions in multiple sclerosis. J. Neurol. Sci. 178, 81–87 (2000).
[5] Parry, A. et al. White matter and lesion T1 relaxation times increase in parallel and correlate with disability in multiple sclerosis. J. Neurol. 249, 1279–1286 (2002).
[6] Reitz, S. C. et al. Multi-parametric quantitative MRI of normal appearing white matter in multiple sclerosis, and the effect of disease activity on T2. Brain Imaging Behav. 11, 744–753 (2017).
[7] Liao, C. et al. 3D MR fingerprinting with accelerated stack-of-spirals and hybrid sliding-window and GRAPPA reconstruction. Neuroimage 162, 13–22 (2017).
[8] Wang, F. et al. 3D Echo Planar Time-resolved Imaging (3D-EPTI) for ultrafast multi-parametric quantitative MRI. Neuroimage 250, 118963 (2022).
[9] Cao, X. et al. Optimized multi-axis spiral projection MR fingerprinting with subspace reconstruction for rapid whole-brain high-isotropic-resolution quantitative imaging. Magn. Reson. Med. 88, 133–150 (2022).
[10] Kvernby, S. et al. Simultaneous three-dimensional myocardial T1 and T2 mapping in one breath hold with 3D-QALAS. J. Cardiovasc. Magn. Reson. 16, 102 (2014).
[11] Fujita, S. et al. Accelerated Isotropic Multiparametric Imaging by High Spatial Resolution 3D-QALAS With Compressed Sensing. Investigative Radiology vol. 56 292–300 (2021).
[12] Ma, D. et al. Magnetic resonance fingerprinting. Nature 495, 187–192 (2013).
[13] Tamir, J. I. et al. T2 shuffling: Sharp, multicontrast, volumetric fast spin-echo imaging. Magn. Reson. Med. 77, 180–195 (2017).
[14] Iyer, S. et al. Wave-encoding and Shuffling Enables Rapid Time Resolved Structural Imaging. arXiv [physics.med-ph] (2021).
[15] Tamir, J. I. et al. Targeted rapid knee MRI exam using T2 shuffling. J. Magn. Reson. Imaging (2019) doi:10.1002/jmri.26600.
[16] Zhao, B. et al. Optimal Experiment Design for Magnetic Resonance Fingerprinting: Cramér-Rao Bound Meets Spin Dynamics. IEEE Trans. Med. Imaging 38, 844–861 (2019).
[17] Lee, P. K., Watkins, L. E., Anderson, T. I., Buonincontri, G. & Hargreaves, B. A. Flexible and efficient optimization of quantitative sequences using automatic differentiation of Bloch simulations. Magn. Reson. Med. 82, 1438–1451 (2019).
[18] Tamir, J. I., Ong, F., Cheng, J. Y., Uecker, M. & Lustig, M. Generalized magnetic resonance image reconstruction using the Berkeley Advanced Reconstruction Toolbox. in ISMRM Workshop on Data Sampling & Image Reconstruction, Sedona, AZ (2016).
[19] Kingma, D. P. & Ba, J. Adam: A Method for Stochastic Optimization. arXiv [cs.LG] (2014).
Figures