0553
Deep kernel method for free-breathing and ungated cardiac MRI reconstruction
Qing Zou1, Sanja Dzelebdzic1, and Tarique Hussain1
1University of Texas Southwestern Medical Center, Dallas, TX, United States
1University of Texas Southwestern Medical Center, Dallas, TX, United States
Synopsis
Keywords: Heart, Machine Learning/Artificial Intelligence, Reconstruction
We introduce a deep kernel model for the recovery of free-breathing and ungated cardiac MRI from highly undersampled measurements. The proposed scheme uses the cascade of two deep convolutional neural networks for the kernel representation of images. The parameters of the two CNNs in the proposed method are learned from the undersampled measurements directly in this work and hence the framework is unsupervised. The main benefits of the proposed scheme are (a) the elimination of the empirical choice of the feature map and kernel function in the kernel method, and (b) the unsupervised nature of the proposed framework.Background
In this work, we are interested in the reconstruction of free-breathing and ungated cardiac MRI. In this work, we propose an unsupervised deep learning-based reconstruction method for free-breathing and ungated cardiac MRI from the highly undersampled k-t space data, which is acquired using spiral k-space trajectories. Specifically, we propose a deep kernel representation method for reconstructing the real-time free-breathing and ungated cardiac MRI. We show that the kernel representation for images can be implemented by the cascade of two CNNs. The parameters in the CNNs can be learned directly from the undersampled data; hence, no fully sampled training data is needed. This helps remove the barrier to using the deep-learning-based reconstruction method for situations where fully sampled training data is not accessible. Another advantage of the proposed method is that the feature maps and the kernel functions are realized by CNNs and hence are learnable from the data. This avoids the manual selection of the feature maps and the kernel functions as well as the parameters in the functions, and hence the proposed method offers improved reconstruction performance compared to the classical kernel methods [1,2].Methods
The focus of this work is to reconstruct the free-breathing and ungated cardiac MR images in the time series from highly undersampled k-t space measurements. In this work, we will use the kernel method for image reconstruction. This means that we represent the images using kernel representation [3]. Specifically, for the image frame $$$\mathbf{x}_i$$$ in the time series, the intensity at location $$$m$$$ can be represented as: $$ x_m = \sum_{n\in N_m} \alpha_n\mathcal{K}(x_m,x_n), $$ where $$$$N_m$$$ is a user-predefined neighborhood of $$$m$$$. $$$\mathcal{K}(x_m,x_n)$$$, which is defined by the inner product of the features $$$\varphi_m$$$ and $$$\varphi_n$$$, is the kernel function.In this work, we propose to implement the feature map as a deep CNN. The feature map $$$\Phi$$$ is applied to the prior images to get the feature vector $$$\varphi$$$ with pre-determined length $$$\ell$$$ for each pixel location. We then implement $$$\Phi_{\theta}$$$ using a U-net, as illustrated in Fig. 1 (a). The learnable parameters in the CNN are denoted by $$$\theta$$$. We implement the feature extraction operator as a deep CNN here because it has been shown that CNN provides better performances for automatic feature extraction. Once the feature operators are defined, a well-defined kernel is then needed for the kernel methods. We implement the kernel function as a convolutional layer in this work. We define $$ \mathcal{K}_{m,n} = \varphi_m * \tilde{\varphi_n},$$ where $$$\tilde{\varphi_n}$$$ is the intrinsic features in the convolutional layer. $$$\tilde{\varphi_n}$$$ is learned directly from the data. The kernel matrix $$$\mathbf{K} = [\mathcal{K}_{m,n}]$$$ and we have the following image representation: $$\mathbf{x}_i = \mathbf{K}\alpha_i,\quad i=1,\cdots,M.$$ The multiplication $$$\mathbf{K}\alpha_i$$$ can be implemented by a fully-connected layer so that $$$\alpha_i,\,\, i=1,\cdots,M$$$ can be learned from the data. The full illustration of this deep kernel representation can be seen in Fig. 1.
We now have the following deep kernel representation for the free-breathing and ungated cardiac MRI representation: $$\mathbf{x}_i = \left(\Phi_{\theta}(\mathcal{A}^H\mathbf{b})*\tilde{\varphi}\right)\alpha_i,\quad i=1,\cdots,M.$$ The parameters $$$\theta, \tilde{\varphi}, \alpha_i$$$ can be learned from only the undersampled measurements based on the following cost function: $$ \mathcal{C}(\theta, \tilde{\varphi}, \alpha) = \sum_{i=1}^M\left(\underbrace{||\mathcal{A}_i\left[(\Phi_{\theta}(\mathcal{A}^H\mathbf{b})*\tilde{\varphi})\alpha_i\right] - \mathbf{b}_i||^2}_{\scriptsize \mbox{data term}} + \underbrace{\lambda\cdot TV[(\Phi_{\theta}(\mathcal{A}^H\mathbf{b})*\tilde{\varphi})\alpha_i]}_{\scriptsize \mbox{image regularization}}\right).$$ Here $$$TV$$$ denotes the total variation regularization and $$$\lambda$$$ is chosen to be $$$0.01$$$ in this work. All the parameters are initialized as random and ADAM optimization is used for updating the parameters.
Results
We first show the ability of the deep kernel method to reconstruct free-breathing and ungated cardiac MRI. We also show the comparison between the reconstructed free-breathing (FB) images and the fully-sampled breath-held (BH) images. In Fig. 2, we show the end-diastolic phase and the end-systolic phase of one slice reconstructed using the deep kernel method. The reconstructed FB images are compared with the fully sampled BH images acquired using the bSSFP sequence and FGRE sequence. We also showed the image quality assessment done in a blinded fashion by two medical experts in Fig. 3. Image quality assessment is based on the scoring criteria scales from 1 to 4 (1 -- non-diagnosable; 2 -- diagnosable with average image quality; 3 -- diagnosable with adequate image quality; 4 -- excellent image quality).For the reconstruction of the free-breathing and ungated cardiac MRI, we also compare the proposed deep kernel method with a state-of-the-art kernel reconstruction method "SToRM", which was proposed in [4]. Fig.4 showed the visual comparison and quantitative comparison of the reconstructed images using the two methods. The end-diastolic and the end-systolic phases from one slice was shown in the figure.
Conclusion
In this work, we introduced a deep kernel method for the reconstruction of free-breathing and ungated cardiac MRI from highly undersampled measurements. In the proposed deep kernel method, we used a CNN for the implementation of the feature extraction operator, and a one-layer CNN is used for the kernel matrix calculation. One benefit of the deep kernel method is the elimination of the manual choices for the feature map and the kernel function. Besides, the deep kernel method avoids the manual tuning of the parameters in the kernel functions. This results in the improved performance of the deep kernel method.Acknowledgements
No acknowledgement found.References
[1] U. Nakarmi et. al., "A kernel-based low-rank (KLR) model for low-dimensional manifold recovery in highly accelerated dynamic MRI", IEEE TMI, 2017.
[2] O. Arif et. al., "Accelerated dynamic MRI using kernel-based low rank constraint", J. Med. Syst, 2019.
[3] B. Schölkopf et. al., "Learning with kernels: support vector machines, regularization, optimization, and beyond", MIT press, 2002.
[4] A. H. Ahmed et. al., "Free-breathing and ungated dynamic mri using navigator-less spiral storm", IEEE TMI, 2020.
Figures

Fig. 1. Illustration
of the proposed deep kernel method for free-breathing and ungated cardiac MRI
reconstruction. (a) shows the structure of the feature extraction network. (b)
is the proposed deep kernel representation.

Fig. 2. Visual
comparison between the FB images and BH images. The three columns are the BH
images acquired using the bSSFP sequence, reconstructed FB images, and BH
images acquired using the FGRE sequence.
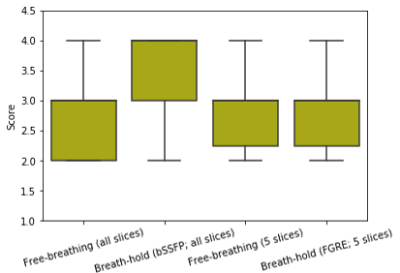
Fig. 3. We reconstructed all the
short-axis slices acquired using the GRE sequence from 5 subjects.
Fully-sampled BH images for all the slices using the bSSFP sequence were also
acquired and one middle slice using the product FGRE sequence
was also collected. The FB images from all the slices received an average score
of 2.7 and the fully-sampled images using the bSSFP sequence got an
average score of 3.6. The fully-sampled BH images using the FGRE
sequence received an average score of 2.9, and the FB images corresponding to
these 5 slices got an average score of 2.8.
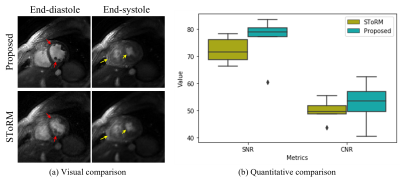
Fig. 4. Comparisons
with state-of-the-art kernel method. (a) shows the visual comparison between
the proposed method and the SToRM method. From the images, we can see that the
proposed reconstruction scheme can provide images with sharper edges and the
papillary muscles are more visible (illustrated by the red arrows in the
images). Furthermore, we can see that the
proposed scheme provides reduced motion artifacts and the RV free-wall is more
clear (illustrated by the yellow arrows in the images). The improved image quality
is also confirmed by the quantitative results, as shown in (b).
DOI: https://doi.org/10.58530/2023/0553