Synopsis

Keywords: Heart, Heart

Real-time cine CMR is an ECG-free free-breathing alternative for functionally assessing the heart. To achieve sufficient spatio-temporal resolutions, these require rapid imaging, e.g. compressed sensing (CS) with radial trajectories. However, at high accelerations, CS may suffer from residual aliasing and temporal blurring. Recently, deep learning (DL) reconstruction has gained immense interest for fast MRI. Yet, for free-breathing real-time cine, where subjects have different breathing and cardiac motion patterns, database learning of spatiotemporal correlations has been difficult. Here, we propose a physics-guided DL reconstruction trained in a subject-specific manner. Proposed method improves image quality compared to database-trained DL and conventional methods.

INTRODUCTION

Real-time cine CMR is an ECG-free free-breathing alternative to the clinical gold-standard ECG-gated, breath-hold cine MRI for evaluating cardiac function¹. It is primarily used in patients who cannot hold their breaths or with arrhythmias, or during exercise stress^2,3. In order to achieve high spatio-temporal resolution in real-time cine CMR, accelerated imaging, such as compressed sensing (CS), is often required, typically in conjunction with radial trajectories that exhibit incoherent artifacts, and flexibility with retrospectively adjusting temporal resolution^4,5,6. Cartesian acquisitions with uniform undersampling are also used clinically, albeit at lower spatio-temporal resolutions^7,8. Furthermore, CS reconstruction may suffer from residual aliasing and blurring at higher acceleration rates. Recently, deep learning (DL) reconstruction has shown promising results for highly-accelerated MRI, improving on parallel imaging and CS^9,10. Yet, learning a spatiotemporally-regularized reconstruction for free-breathing real-time cine CMR, where subjects exhibit varying breathing and cardiac motion patterns, has been difficult. In this work, we use subject-specific zero-shot¹¹ physics-guided DL (PG-DL) without a training database or ground-truth data to improve highly accelerated real-time cine CMR. Results on retrospectively 7.2-fold accelerated data show substantially improvement compared to existing methods.

METHODS

Subject-Specific PG-DL Reconstruction:

Regularized MRI reconstruction is formulated as:

$$\mathbf{x}=\arg \min _{\mathbf{x}}\left\|\mathbf{y}_{\Omega}-\mathbf{E}_{\Omega} \mathbf{x}\right\|_2^2+{\mathscr R}(\mathbf{x}), \quad\quad\quad (1)$$

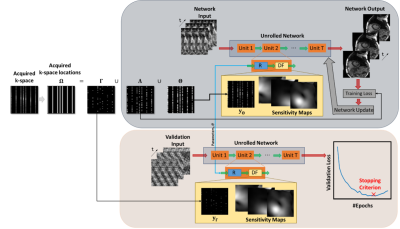
where $$$\mathbf{y}_{\Omega}$$$ is the acquired multi-coil k-space, Ω is the undersampling pattern,$$$\mathbf{E}_{\Omega}$$$ is the multi-coil encoding operator, $$$\mathbf{x}$$$ is the underlying image and $$${\mathscr R}$$$ is a regularizer. PG-DL methods solve this via algorithm unrolling¹², alternating between conventional data-fidelity and a proximal operator, implicitly implemented via neural networks. While supervised learning with a fully-sampled reference is commonly used, recently self‐supervised learning, e.g. SSDU¹², which does not require fully-sampled training data has been proposed. SSDU splits Ω into two disjoint sets $$$\Theta$$$ and $$$\Lambda$$$, where $$$\Theta$$$ enforces data-fidelity in the PG-DL network, while $$$\Lambda$$$ is used to define k-space loss. More recently, zero-shot self-supervised learning (ZS-SSDU)¹¹ has been proposed for training a PG-DL network on a single undersampled dataset. In this approach, Ω is split into three disjoint sets as $$$\Omega = \Theta \cup \Lambda \cup \Gamma$$$ where $$$\Gamma$$$ is an additional set for defining a k-space self-validation loss for early stopping to avoid overfitting (Fig. 1)¹¹. Using multi-mask data-augmentation¹³ that partitions $$$\Omega$$$ \ $$$\Gamma$$$ into K disjoint pairs $$$( \Omega_k,\Gamma_k)$$$, ZS-SSDU loss is given as:
$$\min _{\boldsymbol{\theta}} \frac{1}{K} \sum_{\mathrm{k}=1}^K {\mathscr L}\left(\mathbf{y}_{\Lambda_{\mathrm{k}^{\prime}}}, \mathbf{E}_{\Lambda_{\mathrm{k}}}\left({\mathscr f}\left(\mathrm{y}_{\Theta_{\mathrm{k}^{\prime}}} \mathbf{E}_{\Theta_{\mathrm{k}}} ; \boldsymbol{\theta}\right)\right)\right), \quad\quad\quad (2)$$

where $$$\boldsymbol{\theta}$$$ denotes the network parameters, $$${\mathscr f}(\cdot,\cdot)$$$ denotes the PG-DL network output and $$${\mathscr L}(\cdot,\cdot)$$$ is the training loss. This is supplemented with a self-validation loss on $$$\Gamma$$$ which is calculated at each epoch j from the current network weights specified by $$$\boldsymbol{\theta}^{(j)}$$$ as follows:

$${\mathscr L}\left(\mathbf{y}_{\Gamma}, \mathbf{E}_{\Gamma}\left({\mathscr f}\left(\mathbf{y}_{\Omega \backslash \Gamma}, \mathbf{E}_{\Omega \backslash \Gamma} ; \boldsymbol{\theta}^{(j)}\right)\right)\right). \quad\quad\quad (3)$$

When training on a single dataset, training loss in Eq. (2) keeps decreasing, and training is stopped once self-validation loss in Eq. (3) starts increasing to avoid overfitting¹¹.

Imaging Experiments:

Real-time imaging datasets were acquired at 1.5T on 11 subjects with time-interleaved Cartesian acquisitions at acceleration R=4 using a bSSFP sequence. Relevant imaging parameters: resolution=2.25×2.93mm², FOV=360×270mm², temporal resolution=39ms and slice-thickness=8mm (12 slices). Real-time data were further retrospectively undersampled to R=7.2 by sampling every 8^th line, while keeping the closest k_y line to central k-space for each time-frame for a total of 10 lines per time-frame.

PG-DL Implementation Details:

Subject-specific regularization across all time-frames was performed using ZS-SSDU¹¹ (Fig. 1) on a test subject. A 3D PG-DL network unrolled ADMM algorithm for 10 iterations. A 3D ResNet¹⁴ was used for the regularizer, with 50 time-frames in its input and 128 channels in hidden layers. Conjugate gradient was used for data fidelity¹⁵. Adam optimizer was used with LR=$$$2\cdot10^{-4}$$$ and mixed normalized $$$\ell_1-\ell_2$$$ loss¹² were used. R adjacent frames were used to generate calibration data in a sliding-window manner^16,17, on which coil sensitivity maps were generated¹⁸. 20% of $$$\Omega$$$ was uniformly randomly selected for $$$\Gamma$$$.

For R=7.2 data, comparisons were made to TGRAPPA¹⁵, locally-low-rank (LLR) regularized reconstruction¹⁹ and database-trained (10 subjects for training, 1 unseen subject for testing) SSDU¹². TGRAPPA¹⁵ at standard acceleration R=4 was used for visual image quality comparisons.

RESULTS

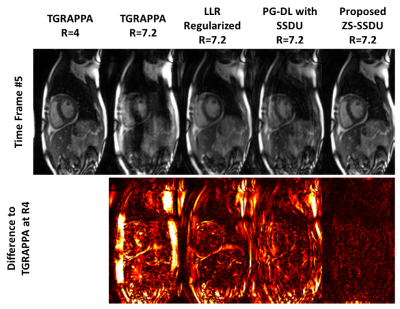
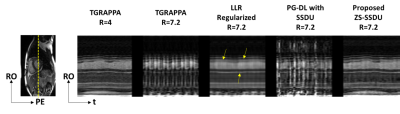
Fig. 2 shows an example time-frame reconstructed with different techniques. TGRAPPA and database-trained SSDU show substantial residual aliasing, former due to the high in-plane acceleration, and latter due to varying spatio-temporal correlations among subjects in the database. LLR-regularized reconstruction reduces residual aliasing albeit with temporal blurring. Proposed approach improves upon all methods and successfully suppresses aliasing. Difference images to TGRAPPA at R=4 show that proposed method only exhibits noise-like differences, whereas all other methods reveal structural differences.

Fig. 3 depicts representative temporal intensity profiles. Temporal variations due to cardiac and respiratory motion are not preserved in TGRAPPA and SSDU, while LLR-regularized reconstruction exhibits temporal blurring. Proposed technique closely matches the R=4 data in terms of temporal intensity profiles.

DISCUSSION AND CONCLUSIONS

In this study, we proposed a subject-specific zero-shot PG-DL approach that does not require a training database or reference data for highly-accelerated real-time cine CMR, improving on existing methods. Use of zero-shot training enables regularization over spatio-temporal domain, where subject-specific breathing and cardiac motions are reliably learned without temporal blurring. Further studies with prospective higher accelerations at improved spatio-temporal resolutions are warranted.

Acknowledgements

Funding: Grant support: NIH R01HL153146, NIH P41EB027061, NIH R21EB028369, NSF CCF-1651825.