0542
Multiband T-Hex spirals for rapid and SNR-efficient diffusion-weighted MRI1Cardiff University Brain Research Imaging Centre (CUBRIC), Cardiff University, Cardiff, United Kingdom, 2Leeds Institute of Cardiovascular and Metabolic Medicine, University of Leeds, Leeds, United Kingdom
Synopsis
Keywords: New Trajectories & Spatial Encoding Methods, New Trajectories & Spatial Encoding Methods
Diffusion weighted imaging (DWI) for advanced modelling of tissue microstructure is notoriously short in SNR and requires long scan times. In this work we boost the SNR of DWI by combining highly efficient T-Hex sampling with multiband imaging and spiral readout schemes. This allows for an unprecedented SNR efficiency and holds promise for advanced microstructural scans especially in clinical populations.Introduction
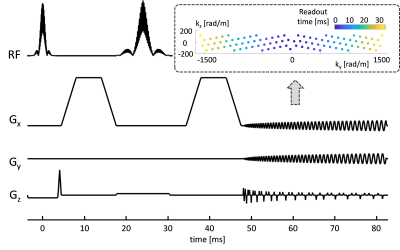
The current trend towards ever more intricate models of brain tissue microstructure calls for cumbersome and often lengthy diffusion MRI (dMRI) experiments. For such extensive data acquisition schemes, efficient spatial encoding is vital to mitigate adverse effects from patient motion. Furthermore, short echo-times (TE) can help to mitigate the otherwise low SNR in dMRI experiments (1–3). Spiral k-space trajectories achieve the shortest possible TEs by acquiring the k-space centre in the beginning of the readout, and offer efficient k-space sampling by making very good use of the gradient system. Leveraging additionally the encoding capabilities of the receive coils in the 3rd dimension calls for 3D or Multiband (MB) imaging. Recently, tilting of the hexagonal grid (T-Hex) underlying 3D k-space for stacked trajectories has enabled particularly time-efficient acquisition of 3D images (4). However, except for very low spatial resolutions, 3D imaging requires multiple shots to acquire the entire k-space, which is unfavourable for dMRI, where shot-to-shot motion can lead to severe image artifacts and steady-state conditions favour longer repetition times. Here, for the first time, we combine a single-shot T-Hex spiral readout with MB pulses, and, on top, utilize a strong gradient system for ultra-efficient dMRI.Methods
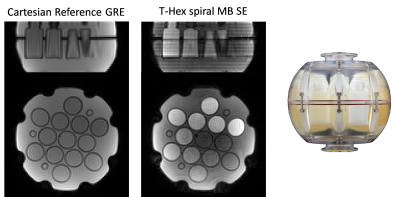
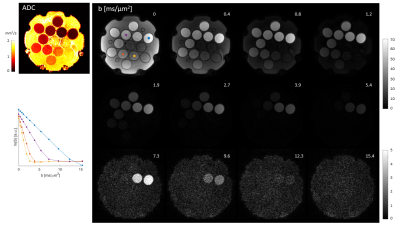
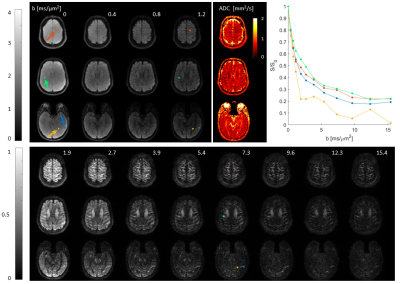
Scans of a diffusion phantom (CaliberMRI, Boulder, USA) and of a healthy volunteer (male, age 28) were performed on a 3T Connectom scanner (Siemens Healthcare GmbH, Erlangen, Germany) using a 32-channel receive array. Sequence parameters (Fig. 1): phase-optimized excitation and refocusing pulses (5–7), Stejskal-Tanner Diffusion encoding (8), T-Hex spiral readouts (generating vector v = [2,1]), b = 0, 0.385, 0.771, 1.156, 1.927, 2.697, 3.854, 5.395, 7.322, 9.634, 12.331, 15.414 ms/μm2 in the LR direction, TE = 48 ms, TR = 1 s, 3 simultaneously excited slices, 30 slices in total, 3 mm slice thickness, no slice gap, 2 mm in-plane resolution, 22 cm in-plane FOV, overall undersampling factor R = 4.6, 34 ms readout duration, 3 initial dummy scans, total acquistion time = 15 s. Field dynamics were measured with a dedicated camera (Skope Magnetic Resonance Technologies, Zurich, Switzerland) and incorporated up to 3rd order in the image reconstruction, which was based on a cg-SENSE (9) algorithm including off-resonance correction (4,10) (skope-i). Coil sensitivity and B0 maps were computed from a Cartesian multi-echo gradient echo (GRE) prescan. ADC maps were computed from the three diffusion weightings < 1 ms/μm2. Signal decay curves were studied for four manually drawn ROIs in the diffusion phantom, each covering one vial, and for four single voxels in-vivo.Results
The resulting images (Fig. 2-4) exhibit an overall high visual fidelity. Spatial deformation can be seen on both the reference and T-Hex spiral scan (Fig. 2). This stems from gradient-non-linearities that are a known feature of the Connectom scanner (11) and can readily be corrected in the post-processing of the data (12). Slight slice-to-slice intensity variations in the T-Hex spiral MB Spin-echo (SE) are probably due to too few initial dummy scans so that a steady state is not yet reached. Ringing artefacts occur only in places of steep off-resonance changes (e.g. near the nasal cavities in the lowermost slice shown in Fig. 4). Notably the SNR suffices to see remaining signal (e.g in the corpus callosum) and clearly discernible WM/GM boundaries up to the higest b-value without averaging.Discussion
We successfully demonstrated for the first time MB spiral imgaging, enhanced by a T-Hex sampling scheme. We showed its application in dMRI where it substantially enhances imaging speed and SNR efficiency. A comparable 2D spiral sequence would require an acquisition time 2.3 times longer. And previous work on the same gradient system utilizing Multiband imaging reported for example 143 resolved kilo-Voxel/second (kVox/s) for b = 10 ms/μm2 (13), 214 kVox/s for b = 10 ms/μm2 (14) or 300 kVox/s for b = 10.5 ms/μm2 (15), whereas in this work, we achieve 363 kVox/s for b = 15.4 ms/μm2.The key feature of the T-Hex scheme is to allow as much k-space volume to be sampled per shot as possible to minimize the number of shots needed. This feature is particularly relevant for dMRI with high b-values and long diffusion times, since that implies large time overheads per shot (4). However, T-Hex dMRI becomes only feasible with the MB single-shot version of T-Hex presented in this work. Nevertheless, the MB single-shot version of T-Hex can likewise be applied to other contrasts such as BOLD fMRI (16). There, it might facilitate slice-timing correction (17,18). However, compared to the 3D version of T-Hex, this comes at the expense of increased SAR levels due to the more challenging RF pulses and it should be noted that regarding the spatial encoding, the feasible acceleration for 3D T-Hex and for MB T-Hex is the same. Hence, the MB approach is preferable to regular 3D imaging only when shot-to-shot inconsistencies favor single-shot acquisition or steady-state considerations favor longer TR.
Future work should investigate the integration with more time-efficient (7,19) and yet off-resonance-robust MB pulses and subsequently examine the performance of the new method in expansive dMRI experiments.
Acknowledgements
The data were acquired at the UK National Facility for In Vivo MR Imaging of Human Tissue Microstructure funded by the EPSRC (grant EP/M029778/1), and The Wolfson Foundation, and supported by a Wellcome Trust Investigator Award (096646/Z/11/Z) and a Wellcome Trust Strategic Award (104943/Z/14/Z)References
1. Wilm BJ, Hennel F, Roesler MB, Weiger M, Pruessmann KP. Minimizing the echo time in diffusion imaging using spiral readouts and a head gradient system. Magn. Reson. Med. 2020;84:3117–3127 doi: 10.1002/mrm.28346.
2. Lee Y, Wilm BJ, Brunner DO, et al. On the signal-to-noise ratio benefit of spiral acquisition in diffusion MRI. Magn. Reson. Med. 2021;85:1924–1937 doi: 10.1002/mrm.28554.
3. Mueller L, Rudrapatna SU, Tax CMW, Wise RG, Jones DK. Diffusion MRI with b=1000 s/mm2 at TE < 22 ms using single-shot spiral readout and ultra-strong gradients: Implications for microstructure imaging. In: Proc. Intl. Soc. Mag. Reson. Med. 27. ; 2019. p. 0766.
4. Engel M, Kasper L, Wilm B, et al. T-Hex: Tilted hexagonal grids for rapid 3D imaging. Magn. Reson. Med. 2021;85:2507–2523 doi: 10.1002/mrm.28600.
5. Hennig J. Chemical shift imaging with phase-encoding RF pulses. Magn. Reson. Med. 1992;25:289–298 doi: 10.1002/mrm.1910250207.
6. Wong E. Optimized phase schedules for minimizing peak RF power in simultaneous multi‐slice RF excitation pulses. In: 2012 ISMRM Annual Meeting Proceedings. Melbourne, Australia; 2012. p. 2209.
7. Abo Seada S, Price AN, Schneider T, Hajnal JV, Malik SJ. Multiband RF pulse design for realistic gradient performance. Magn. Reson. Med. 2019;81:362–376 doi: 10.1002/mrm.27411.
8. Stejskal EO, Tanner JE. Spin Diffusion Measurements: Spin Echoes in the Presence of a Time‐Dependent Field Gradient. J. Chem. Phys. 1965;42:288–292 doi: 10.1063/1.1695690.
9. Pruessmann KP, Weiger M, Börnert P, Boesiger P. Advances in sensitivity encoding with arbitrary k-space trajectories. Magn. Reson. Med. 2001;46:638–651 doi: 10.1002/mrm.1241.
10. Wilm BJ, Barmet C, Pavan M, Pruessmann KP. Higher order reconstruction for MRI in the presence of spatiotemporal field perturbations. Magn. Reson. Med. 2011;65:1690–1701 doi: 10.1002/mrm.22767.
11. Rudrapatna U, Parker GD, Roberts J, Jones DK. A comparative study of gradient nonlinearity correction strategies for processing diffusion data obtained with ultra‐strong gradient MRI scanners. Magn. Reson. Med. 2021;85:1104–1113 doi: 10.1002/mrm.28464.
12. Doran SJ, Charles-Edwards L, Reinsberg SA, Leach MO. A complete distortion correction for MR images: I. Gradient warp correction. Phys. Med. Biol. 2005;50:1343–1361 doi: 10.1088/0031-9155/50/7/001.
13. Setsompop K, Kimmlingen R, Eberlein E, et al. Pushing the limits of in vivo diffusion MRI for the Human Connectome Project. NeuroImage 2013;80:220–233 doi: 10.1016/j.neuroimage.2013.05.078.
14. Fan Q, Witzel T, Nummenmaa A, et al. MGH–USC Human Connectome Project datasets with ultra-high b-value diffusion MRI. NeuroImage 2016;124:1108–1114 doi: 10.1016/j.neuroimage.2015.08.075.
15. Setsompop K, Cohen-Adad J, Gagoski BA, et al. Improving diffusion MRI using simultaneous multi-slice echo planar imaging. NeuroImage 2012;63:569–580 doi: 10.1016/j.neuroimage.2012.06.033.
16. Zahneisen B, Poser BA, Ernst T, Stenger VA. Simultaneous Multi-Slice fMRI using Spiral Trajectories. NeuroImage 2014;92:8–18 doi: 10.1016/j.neuroimage.2014.01.056.
17. Henson R, Rugg MD, Friston KJ. The choice of basis functions in event-related fMRI. NeuroImage 2001;13:149 doi: 10.1016/S1053-8119(01)91492-2.
18. Bianchi S, Heinzle J, Engel M, Kasper L, Pruessmann KP. Reconstruction of 3D EPI timeseries including a correction of different acquisition times. In: Proceedings of the Joint Annual Meeting ISMRM-ESMRMB. London, United Kingdom; 2022. p. 2341.
19. Hargreaves BA, Cunningham CH, Nishimura DG, Conolly SM. Variable-rate selective excitation for rapid MRI sequences. Magn. Reson. Med. 2004;52:590–597 doi: 10.1002/mrm.20168
Figures