Synopsis

Keywords: Data Acquisition, Data Acquisition, Non-Cartesian; SPARKLING

Non-Cartesian sampling patterns allow for highly accelerated MRI exams at the cost of exacerbated and more complex artifacts, each impacting image quality in unique ways. Patient-induced B0 field inhomogeneities can notably cause distortions and blurring, but some trajectories are by design more robust to them. We propose to retrospectively benchmark 16 different non-Cartesian sampling patterns with high acceleration factor (AF=20) and realistic off-resonance artifacts over 9 volumes acquired at 3T with 0.6 mm isotropic spatial resolution. SPARKLING and spiral-based trajectories achieve higher image quality scores, but only the former shows robustness to off-resonance effects through the MORE-SPARKLING extension.

Introduction

Cartesian sampling patterns are widely used in research and clinical settings because of their simplicity, associated with the uncontested efficiency of parallel imaging reconstruction methods such as GRAPPA and CAIPIRINHA. However, further undersampling the k-space using higher acceleration factors (AF) requires more degrees of freedom, as provided by non-Cartesian¹ patterns. Such trajectories, already used in Sodium and cardiac imaging^2,3, or recently for SWI, FLAIR, SPACE⁴ and other MR sequences, rely on magnetic gradients played in multiple directions during readouts. This principle allows for more arbitrary trajectories and longer observation windows, both reducing the amount of total shots needed. But it also exacerbates various artifacts and in more complex ways as compared to Cartesian trajectories. Besides undersampling artifacts, off-resonance effects commonly induced by air/tissue magnetic susceptibility gaps in the human brain can impact significantly image quality with signal loss, geometric distortions and blurring. This impact changes depending on the sampling pattern, and therefore we propose to retrospectively observe and benchmark 16 different non-Cartesian trajectories, picked or generalized from existing literature, with high acceleration factor (AF=20) and realistic off-resonance artifacts.

Materials and methods

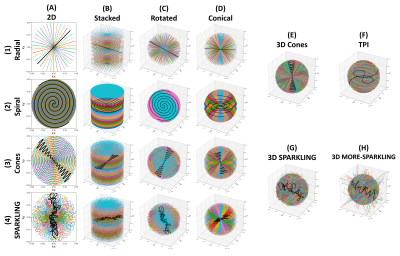
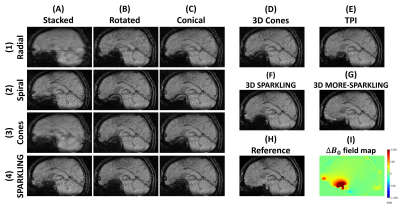
Retrospective results are obtained by projecting reference images onto arbitrary trajectories with a non-uniform fast Fourier transform to simulate raw data, assuming images with sufficiently high quality and low artifacts. A total of 9 volumes were acquired for reference at 3T on different healthy volunteers with a Cartesian 3D GRE sequence and the following parameters: acquisition time (TA): 15min13s (iPAT4), resolution: 0.6mm isotropic, matrix size: 384x384x208, TE/T_obs/TR: 20/20/37ms. An additional B₀ map was acquired with the following parameters: TA: 2min43s, resolution: 2mm isotropic, same FOV, TE1/TE2: 4.92/7.38ms.

Different in-out 3D trajectories were generated to match an AF=20 (approx. 384x208/20 shots) with N_s=2048 samples per shot while respecting the following scanner constraints: raster time: 10µs, maximum gradient amplitude: 40mT/m and slew rate: 100T/m/s. Most trajectories were obtained by expanding 2D patterns composed of N_c/p shots into 3D patterns of N_p planes, as represented in Fig.1 (A-D): radial, spiral, cones and 2D SPARKLING⁵ planes were stacked (N_p=208, N_c/p=19), rotated (N_p=189, N_c/p=21) or reshaped into cones (N_p=189, N_c/p=21). Several spirals have been considered (based on the polar equation r=a+bxθ1/c) to finally retain the Archimedean spiral (c=1) with a maximized number of revolutions (n_r=3) per shot. Similarly, 2D cones were parameterized to maximize the number of zigzags per shot (n_z=7) with some overlap between shots (n_o=2). Additionally, native 3D trajectories were studied (Fig.1 (E-H)): 3D cones (n_z=15, n_o=2), TPI² (30% radial center), SPARKLING⁶ and MORE-SPARKLING⁷ (both with densities optimized⁵ with τ=0.67 and d=2).

Image reconstructions were performed iteratively using the pysap-mri^8,9 package with the FISTA algorithm and a soft thresholding regularization in the wavelet domain (Symlet8, λ=1e-1, 20 iterations). The pseudo-Fourier operator introduced in [10] was used with the acquired B0 maps and a pre-computed density compensation¹¹ to produce the off-resonance artifacts from the reference images.

Results

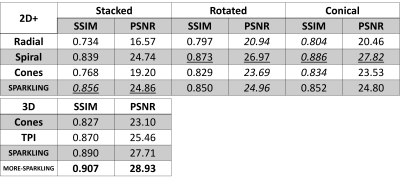
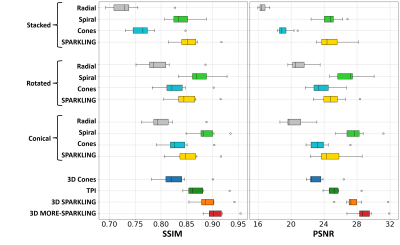
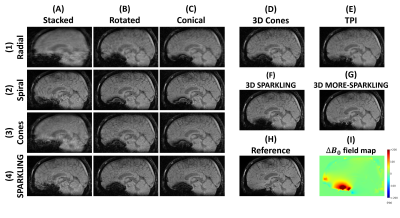
The SSIM and PSNR scores are given in Figs.2-3 and images in Figs.4-5 for different volunteers. MORE-SPARKLING provides the highest scores with margin (+0.017 SSIM; +1.11 PSNR compared to following competitors), followed by 3D SPARKLING and conical spirals. Several observations could be reported: Firstly, stacked implementations generally perform worse than other setups. It might be explained by the different sampling densities and sub-optimal cylindrical coverage. Note however that GRAPPA could be applied to improve performances, but only to stacked versions. Secondly, and despite the previous observation, 2D SPARKLING achieves similar scores with all extensions. It is again expected to come from the density, optimized for stacks in that case. Fine-tuned versions were not proposed as the 3D SPARKLING version was already assumed to outperform them. Finally, based on Figs.4-5, only MORE-SPARKLING (F) and more lightly TPI (E) show robustness toward signal loss caused by off-resonance. Additionally, some spirals (B2, C2) appear to have more spatially restricted artifacts as compared to other 2D+ patterns, and overall rotated and conical implementations show close artifacts.

Conclusion

Geometric sampling patterns have been proposed for decades with increasingly subtle designs, and many such as spiral-based trajectories were shown to still be competitive today. However, automatically-designed sampling patterns like SPARKLING are unique in their capability to explicitly account for specific criteria as demonstrated for off-resonance robustness with MORE-SPARKLING. Nonetheless, the copious amount of literature that proposed comparable methods over time makes it more urgent and significant to provide regular benchmarks against common baselines. Additional effects like bulk motion are similarly being considered, with new perspectives on time-varying k-space coverage.

Acknowledgements

The concepts and information presented in this abstract are based on research results that are not commercially available. Future availability cannot be guaranteed.