Synopsis

Keywords: Data Acquisition, Pulse Sequence Design, Inhomogeneous field

3D Fast spin echo (FSE) with frequency-modulated (FM) pulses has been introduced for MRI in highly inhomogeneous fields. B₁ dependent phase in FM pulse excitation and refocus was adjusted in the FM-FSE pulse sequence. Refocus flip angles in FM-FSE were determined with prospective extended phase graph (EPG). Proposed flip angle and phase in FM-FSE were validated in EPG simulation and experiments at 3T by introducing a linear inhomogeneous field. Finally, in vivo human brain imaging with T₁- and T₂-weighting was performed using the proposed 3D FM-FSE sequence.

Introduction

Frequency-modulated (FM) pulses can achieve broadband excitation with long pulse width, while amplitude-modulated pulses (e.g. hard, sinc and gaussian) require very short pulse width for broadband excitation. FM pulses have recently been implemented in 3D MP-SSFP for MRI in highly inhomogeneous fields to cover the broad frequencies distributed by the field inhomogeneity¹. Spin echo (SE) is also a well-known sequence for its immunity to the field inhomogeneity. Adiabatic double spin echo, which is the most common SE based technique with FM pulses, requires a pair of adiabatic/FM pulses to rewind the quadratic phase². Therefore, when FM pulses are used in fast spin echo (FSE), even and odd echoes show inconsistent phase so that only even or odd echoes can be used for imaging (or simultaneous 2 k-space acquisitions). In this study, we introduce 3D FM-FSE with consistent phase in even and odd echoes for MRI in highly inhomogeneous fields.

Methods

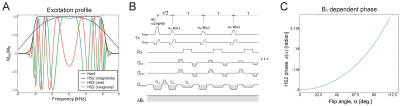
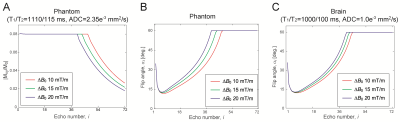
The commonly used clinical 3D FSE sequence (aka SPACE/CUBE) uses a short hard pulse for refocusing without slab selection to minimize echo spacing, τ. While a hard pulse is highly efficient to refocus the magnetization with a short pulse width, it entails a high RF peak power especially when requiring broadband refocusing. For example, a 12-kHz hard pulse (pulse width, pw = 100 µs) requires RF power (B_1max) of 58.7 µT for 90° flip angle, which exceeds the limit of standard clinical MRI systems. A flattened hyperbolic secant pulse (HS2)³ yields a better excitation profile and only requires B_1max = 18.1 µT, although at the expense of pw = 3.6 ms (Fig.1A). In the proposed FM-FSE, an HS2 pulse was used for excitation and refocusing to make even and odd echo phase consistent (Fig.1B). Since FM pulses introduce B₁/flip angle dependent phase to the magnetization, the excitation and refocusing pulse phase was adjusted with the B₁ dependent phase, φ(α) (Fig.1C).

Flip angles in 3D FM-FSE were determined with prospective extended phase graph (EPG)⁴ including diffusion effects^5,6. First, optimal flip angles were calculated with a target of |M_xy/M₀| = 0.08 and a limit of 60° for an agar gel phantom with known parameters (Fig.2A,B). Refocused echo signal intensities matched the target until the flip angle reached the 60° limit. EPG simulations were also performed for experimental validation. For brain imaging, optimal flip angles were separately calculated with the brain parameters at 3T^7,8 (Fig.2C).

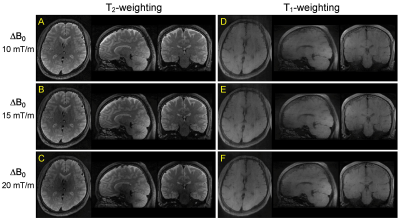
MRI studies were conducted with a Siemens Prisma 3T MRI using a 32ch head coil. The optimal flip angles and B₁ dependent phases were first validated with the agar gel phantom. Then, in vivo human brain T₁/T₂-weighted imaging was performed with healthy volunteers under an IRB approved protocol. Sequence parameters were: τ = 11 ms, TE_eff = 11/396 ms, TR = 900/1800 ms, HS2 excitation and refocus (pw = 3.6 ms and BW_exc = 12 kHz), BW_ro = 40 kHz, echo train length = 40/72, 1.5 mm isotropic resolution and scan time = 4:30/5:00. A linear inhomogeneous field ΔB₀ of 10, 15 or 20 mT/m was turned on during the entire scan with the z channel of the gradient coil set, which was a field inhomogeneity of 61, 92, or 123 kHz over the FOV. The linear inhomogeneous field was partly compensated during excitation and readout to achieve BW_exc and BW_ro by modulating the z gradient amplitude.

Results

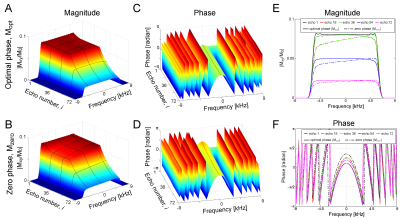
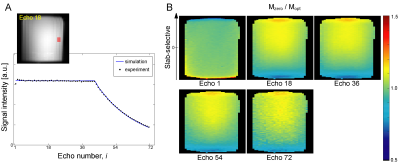
In EPG simulation, the frequency profiles of the refocused echoes attained the desired flatness with the B₁ dependent phase adjustment (M_opt), whereas the profiles without the phase adjustment (i.e. φ(α) = 0, M_zero) showed a mild descending slope towards the low frequency edge (Fig.3A,B). Consistent quadratic phase was observed in all echoes for either M_opt or M_zero (Fig.3C,D). The magnitude profile for M_opt and M_zero was identical at echo 1, but the non-flat intensity profile was clearly seen at echo numbers >18 (Fig.3E). Phase profiles for M_opt matched well for all echoes, but those for M_zero showed minor fluctuation (Fig.3F).

In experiments, echo signal intensities for M_opt showed a good match with the echo signal intensities from EPG simulation (Fig.4A). In profile validation, the echo profiles acquired in experiments for M_opt and M_zero showed similar profile at echo 1, but a consistent intensity drop towards the low frequency edge was observed in M_zero/M_opt at echo 18 and after (Fig.4B), which is consistent to the EPG simulation (Fig.3E). In in vivo brain imaging, SAR was 50-70% of the limit with the vendor provided SAR monitor depending on subjects. 3D FM-FSE provided good T₁/T₂-weighted images by using centric-out and sequential k-space filling (Fig.5).

Discussion

In this study, 1.5-mm isotropic brain imaging was demonstrated with acceptable scan time of 5 min. The proposed 3D FM-FSE can readily be accelerated by introducing partial Fourier reconstruction, parallel imaging and/or compressed sensing reconstruction.

SAR is a serious limitation for 3D FM-FSE in highly inhomogeneous fields. However, most inhomogeneous field MRI systems (e.g. portable MRIs) target lower field strengths (typically <1.5T) than 3T herein. Therefore, this SAR limitation is highly mitigated in actual highly inhomogeneous MRI systems.

Conclusion

3D FSE with frequency-modulated pulse has been introduced for MRI in highly inhomogeneous fields.

Acknowledgements

Supporting grants: NIH U01EB025153 and P41EB027061