0537
Spiral Fast Spin Echo MRI with Interleaved Diffusion Sensitization for Simultaneous ADC and T2 Mapping1Dept.of Radiology, Medical Physics, Medical Center University of Freiburg, Faculty of Medicine, University of Freiburg, Freiburg, Germany, 2German Cancer Consortium (DKTK), Partner Site Freiburg, Freiburg, Germany
Synopsis
Keywords: Pulse Sequence Design, Multi-Contrast
A sequence design is presented based on spiral fast spin echo acquisition with interleaved diffusion sensitization for simultaneous ADC and T2 mapping. With spiral readout trajectories only few echoes need to be acquired per (TE,b) pair allowing to accelerate the acquisition significantly. A phantom experiment with single echo per k-space is shown for T2 and ADC mapping. With a model-based reconstruction both parameter maps can be rapidly reconstructed.
Introduction
Recently, Hennig et. al. (1) demonstrated the feasibility of single shot high-resolution spiral fast spin echo (FSE) at 3T. In this work, spiral FSE is combined with interleaved diffusion sensitization to acquire T2 and ADC maps in a single measurement. The two contrast parameters T2 and ADC are the most relevant parameters in tumor imaging, e.g. in breast, prostate or head&neck cancer (2–4). A simultaneous measurement can decrease the overall acquisition time and circumvents the problem of misregistration due to patient movement or image artifacts (5–9). This work builds on the previously shown radial FSE for simultaneous ADC and T2 mapping (10), by introducing a spiral trajectory which samples a full 2D k-space in each echo of the echo train. Therefore, single shot experiments become feasible.Materials and Methods
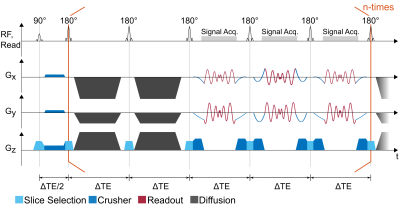
The spiral FSE pulse sequence diagram is shown in figure 1. It consists of a FSE echo train in which crusher gradients are applied on all logical axis directly after the 90° excitation. In the echo train pairs of Stejskal-Tanner diffusion blocks are inserted (11), which are applied on all axis to optimize the maximum available gradient amplitude (and therefore the b-value). During readout spiral-in spiral-out trajectories are applied together with pre- and rephaser gradients which are calculated using spline interpolation taking into account the k-space start-point, end-point as well as the starting- and end-point slew rates to ensure smooth transitions. The spiral trajectories are calculated using the variable density spiral toolbox from Hargreaves (12,13). A soft CMPG-condition is used to reduce the effect of stimulated echoes:$$\int_{t_D}^{t_D+\Delta TE} G(\vec{x},t) \text{d}t \equiv N \int_{t_R}^{t_R+\Delta TE} G(\vec{x},t) \text{d}t ,$$
with $$$t_D$$$ the start time of a diffusion block and $$$t_R$$$ the start time of a readout block. Hence, the gradient-time integral in each part of the diffusion block is an integer multiple of the gradient integral of a readout block (14). Here, N=10 was chosen with regard to the available hardware limits. Data from each echo are assigned to a unique k-space corresponding to the (TE,b) pair of the echo. Reconstruction of the image is performed by a regularized iterative algorithm with an interleaved model optimization as described previously (10,14).
For the experiments, three different $$$\Delta$$$TE=[12,13,14] ms were acquired with 15 successive spiral readouts and interleaved diffusion blocks before the 1st, 4th, 7th and 10th readout (ETL=23). With the three different $$$\Delta$$$TE, the b-value increased by [207, 308, 436] s/mm2 per diffusion block, reaching a maximum b-value of 1744 s/mm2. All experiments were performed on a 3T MRI system with Gmax=80 mT/m (PRISMA, Siemens, Erlangen, Germany).
Numeric phantom experiments were performed to evaluate the reconstruction performance at moderate (15 repetitions) and extreme (1 Repetition=Single Shot) undersampling factors. The results were then tested in a mixed diffusion-T2 phantom, which consists of 12 vials with diffusion values ranging from 0.60 to 2.10 mm2/s and T2 values ranging from 45 to 264 ms (14,15). Finally, a resolution phantom was measured to assess the general image quality. To minimize the effect of noise, all echoes with TE>400 ms and b>900 s/mm2 were excluded from the reconstruction.
Results
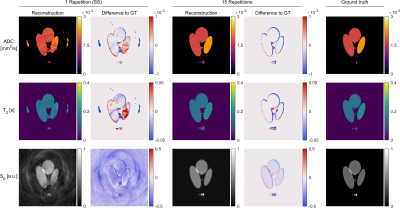
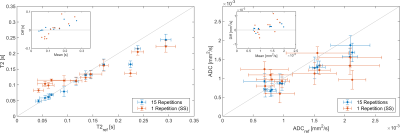
Figure 2 shows the results of the analytic phantom simulation. With 15 repetitions, a maximum ADC / T2 deviation of 1.3% / 2.2% was found in the smallest and 0.2% / 0.06% in the largest connected area on average. The single shot experiment yielded larger deviations of 24.7% / 0.8% and 2.9% / 3.5% respectively.Figure 3 shows the results of the phantom experiment. The S0 image shows blurring toward the image borders. The parameter results in Figure 4 show an overall good correspondence in both ADC and T2 measurements with a reference with deviations below 0.06 s (15 Repetitions)/ 0.1 s (1 Repetition) for T2 and 0.51 mm2s-1 / 1.16 mm2s-1for ADC. Bland-Altmann plots indicate that the spiral sequence generally underestimates T2 for T2<0.12 s and overestimates it for T2>0.12 s. A similar behavior is seen for ADC with a threshold value is around 1 mm2/s. These deviations show a linear behavior.
The resolution phantom (figure 5) shows similar blurring towards the image edges as the parameter phantom. In the single shot experiment, large portions of the structure are masked by artifacts from the spiral readout trajectory.
Discussion and Conclusion
In this work, we developed a spiral trajectory for a fast spin echo sequence with interleaved diffusion encoding for simultaneous ADC and T2 mapping. Accurate parameter mapping was shown in simulation and phantom experiments with data from 15 repetitions, and feasibility of a single shot experiment was tested. In the single shot experiment, the parameter maps could still be reconstructed, but SNR and general image quality are limited. At a TR of 4 s, to guarantee full equilibrium magnetization, the experiment with 15 repetitions could be performed in only 3 minutes, while the single shot experiment only takes 16 seconds (1 dummy cycle, 3 unique $$$\Delta$$$TE). As in conventional FSE, up to 12 slices can be acquired within one TR, given the current setup.Acknowledgements
Grant support by the German Science Foundation (DFG) under grant number 443978314 is gratefully acknowledged.References
1. Hennig J, Barghoorn A, Zhang S, Zaitsev M. Single shot spiral TSE with annulated segmentation. Magn. Reson. Med. 2022;88:651–662 doi: 10.1002/mrm.29224.
2. Steiger P, Thoeny HC. Prostate MRI based on PI-RADS version 2: how we review and report. Cancer Imaging 2016;16:9 doi: 10.1186/s40644-016-0068-2.
3. Kuroki Y, Nasu K. Advances in breast MRI: diffusion-weighted imaging of the breast. Breast Cancer 2008;15:212–217 doi: 10.1007/s12282-008-0050-3.
4. Wiedenmann N, Grosu A-L, Büchert M, et al. The utility of multiparametric MRI to characterize hypoxic tumor subvolumes in comparison to FMISO PET/CT. Consequences for diagnosis and chemoradiation treatment planning in head and neck cancer. Radiother. Oncol. 2020;150:128–135 doi: 10.1016/j.radonc.2020.06.013.
5. Gras V, Farrher E, Grinberg F, Shah NJ. Diffusion-weighted DESS protocol optimization for simultaneous mapping of the mean diffusivity, proton density and relaxation times at 3 Tesla. Magn. Reson. Med. 2017;78:130–141 doi: https://doi.org/10.1002/mrm.26353.
6. Skorpil M, Brynolfsson P, Engström M. Motion corrected DWI with integrated T2-mapping for simultaneous estimation of ADC, T2-relaxation and perfusion in prostate cancer. Magn. Reson. Imaging 2017;39:162–167 doi: 10.1016/j.mri.2017.03.003.
7. Ma S, Nguyen CT, Han F, et al. Three-dimensional simultaneous brain T1, T2, and ADC mapping with MR Multitasking. Magn. Reson. Med. 2020;84:72–88 doi: https://doi.org/10.1002/mrm.28092.
8. Aliotta E, Moulin K, Zhang Z, Ennis DB. Simultaneous Measurement of T2 and Apparent Diffusion Coefficient (T2+ADC) in the Heart With Motion-Compensated Spin Echo Diffusion-Weighted Imaging. Magn. Reson. Med. 2018;79:654–662 doi: 10.1002/mrm.26705.
9. Breutigam N-J, Günther M, Hoinkiss DC, et al. Combined acquisition of diffusion and T2*-weighted measurements using simultaneous multi-contrast magnetic resonance imaging. Magn. Reson. Mater. Phys. Biol. Med. 2022;35:421–440 doi: 10.1007/s10334-021-00976-3.
10. Bielak L, Lottner T, Bock M. Radial Fast Spin Echo MRI with Compressed Sensing for Simultaneous ADC and T2 Mapping. In: Proc. Int. Soc. Mag. Reson. Med. Vol. 29. Virtual Meeting; 2021. p. 4166.
11. Stejskal EO, Tanner JE. Spin Diffusion Measurements: Spin Echoes in the Presence of a Time‐Dependent Field Gradient. J. Chem. Phys. 1965;42:288–292 doi: 10.1063/1.1695690.
12. Lee JH, Hargreaves BA, Hu BS, Nishimura DG. Fast 3D imaging using variable-density spiral trajectories with applications to limb perfusion. Magn. Reson. Med. 2003;50:1276–1285 doi: 10.1002/mrm.10644.
13. Hargreaves BA. Variable-Density Spiral Design Functions. https://mrsrl.stanford.edu/~brian/vdspiral/.
14. Bielak L. Convolutional neural networks for head and neck tumor segmentation in MRI: protocol and sequence optimization. 2022 doi: https://doi.org/10.6094/UNIFR/226301.
15. Rachel T. Parameteroptimierung für die simultane Messung der T2-Relaxation und des Diffusionskoeffizienten in radialen, unterabgetasteten Spin-Echo-Sequenzen [Bachelor thesis]. Fakultät für Mathematik und Physik: Albert-Ludwigs-Universität Freiburg; 2021.
Figures