0494

Frequency and Phase Correction of GABA-edited MR Spectroscopy using Complex-valued Convolutional Neural Network
Hanna Bugler1,2,3,4, Rodrigo Berto1,2,3,4, Roberto Souza1,3,5, and Ashley D. Harris2,3,4
1Biomedical Engineering Department, University of Calgary, Calgary, AB, Canada, 2Department of Radiology, University of Calgary, Calgary, AB, Canada, 3Hotchkiss Brain Institute, University of Calgary, Calgary, AB, Canada, 4Alberta Children's Hospital Research Institute, University of Calgary, Calgary, AB, Canada, 5Electrical and Software Engineering Department, University of Calgary, Calgary, AB, Canada

Synopsis

Keywords: Spectroscopy, Machine Learning/Artificial Intelligence, Brain

Edited Magnetic Resonance Spectroscopy (Edited-MRS) is important for the quantification of ɣ-amino butyric acid (GABA) in vivo. However, during acquisition, data may suffer phase and frequency shifts, which affects the quality of the output spectrum. Frequency and phase correction (FPC) is necessary to account for these shifts, and deep learning models have obtained recent success in this task. Still, current methods do not take into consideration that MRS data is complex-valued. We propose a complex-valued convolutional neural network model for FPC. Our results showed that our model compares favorably against two recently proposed deep learning methods.

Introduction

Magnetic resonance spectroscopy (MRS) is non-invasive method to measure metabolite concentrations in vivo. One metabolite of interest is ɣ-amino butyric acid (GABA), the primary inhibitory neurotransmitter1. Due to its small concentration and that its peaks are overlapped by more abundant metabolites, conventional MRS cannot reliably quantify GABA at 3T. MEscher-GArwood editing (MEGA-PRESS)2 is a technique to isolate the GABA signal by subtracting two subspectra (one edit-ON and one edit-OFF). However, this process results in limited signal-to-noise ratio (SNR) and may lead to subtraction artifacts.

To increase signal quality, preprocessing is needed. Frequency and phase correction (FPC) aims to correct misaligned subspectra. Current methods used for FPC include spectral registration and peak fitting3. Two deep learning (DL) FPC models have recently been proposed to overcome limitations of existing methods. Tapper et al.4 proposed a real-valued multi-layer perceptron for the FPC task. A later work by Ma et al.5 proposed a real-valued convolutional neural network (CNN), which showed improved results. While both models have improved FPC for edited-MRS, these models are real-valued and MRS data is inherently complex-valued, and important phase information is lost when only accounting for the real portion of the spectrum. We propose a complex-valued CNN (C-CNN) which uses complex convolutions6 for FPC. Therefore, in this project, we expand on existing DL FPC methods by evaluating our C-CNN model on simulated data of various quality compared to current DL FPC models.

Materials and Methods

One thousand water suppressed and unsuppressed, edit-ON and edit-OFF, spectra containing 22 metabolites and commonly captured macromolecules were simulated using FID-A7. Noise was added to these simulated subspectra, known as ground truths, to create simulated scans of 320 averages (160 edit-ON and 160 edit-OFF), containing random and linear frequency (-20Hz, +20Hz) and random phase (-90°, 90°) shifts and random Gaussian amplitude noise. This process was repeated at 3 different SNR levels (Poor: 2.5, Fair: 5, Good: 10) and for both water suppression options, resulting in six datasets.

The C-CNN consists of three blocks. The first block consists of two 1D complex-valued convolutional layers with 8 filters and a kernel of size 5 followed by a 1D max pooling layer with pool size of 2. The second block is identical to the first block, but with 16 filters for the convolutions. The third block, subsequent to flattening, consists of two fully connected layers (sizes 1024 and 512) with rectified linear unit activation functions followed by a linear activation output (Figure 1). This network was repeated in series: one for frequency shift predictions followed by a second for phase shift predictions (Figure 2). To fairly compare our model with Ma et al. and Tapper et al. models, the number of parameters in these models was increased to match ours. Figure 3 illustrates the high-level model architectures.

Our model (C-CNN) was compared to Tapper et al. (MLP) and Ma et al. (CNN) models using the same train/test split (80/20) on the six available datasets. Each model was trained for 200 epochs, with a decaying learning rate of 0.001 that halves every 25 epochs, a mean absolute error (MAE) loss function and an Adam optimizer.

Model improvement was measured by the MAE between the predicted and ground truth shifts. Significance of the results was measured at a significance value of 0.05 with a Wilcoxon signed rank test while Cohen’s D was used to measure the effect size.

Results

In all the experiments, our C-CNN outperformed the CNN and MLP models. All results were statistically significant (p< 0.001). CNN was ranked second overall in our experiments. Here, we present the results of the lowest SNR datasets, as they showed the greatest improvement and are the focus of using DL FPC.

For the water suppressed SNR 2.5 dataset (Figure 4), our model reduced the frequency error (MAE =0.183 Hz (C-CNN) vs. 0.269 Hz (CNN)) with a small effect size (Cohen's D= 0.22) and the phase error (MAE = 2.45° (C-CNN) vs. 3.55°(CNN)) with a small to medium effect size (Cohen's D= 0.42).

For the water unsuppressed SNR 2.5 dataset (Figure 4), our model reduced the frequency error (MAE =0.0146 Hz (C-CNN) vs. 0.0177 Hz (CNN)) with a medium effect size (Cohen's D= 0.53) and the phase error (MAE = 0.330° (C-CNN) vs. 0. 579°(CNN)) with a small to medium effect size (Cohen's D= 0.46).

Discussion

Our C-CNN model outperformed the previously proposed DL FPC models under the same training conditions, and model sizes. Leveraging the complex-valued nature of MRS data into complex-valued convolutions proved to be an asset for processing this type of data, especially for phase predictions which are inherently complex.

The magnitude of the improvements ranged from small to medium and were greater for the water suppressed dataset, which is more challenging due to the lack of the large water peak. This indicates that our proposed model is better equipped to overcome challenges associated with lower quality data, such as low SNR datasets, improving upon the objective of the previously proposed models.

Conclusion

In conclusion, the proposed model demonstrated a statistically significant decrease in error on both frequency and phase predictions than existing DL FPC models with a larger effect, on average, on phase data.

Acknowledgements

This study was supported by NSERC Discovery Grants to Roberto Souza and Ashley D. Harris and NSERC Brain Create awards to Rodrigo Berto and Hanna Bugler; the Hotchkiss Brain Institute and Ashley D. Harris holds a Canada Research Chair in MR Spectroscopy in Brain Injury.

References

  1. Stagg CJ, Bachtiar V, Johansen-Berg H. What are we measuring with GABA magnetic resonance spectroscopy?. Commun Integr Biol. 2011;4(5):573-575.
  2. Mescher M, Merkle H, Kirsch J, Garwood M & Gruetter R. Simultaneous in vivo spectral editing and water suppression. NMR Biomed. 1998; 11, 266–272.
  3. Near J, Edden R EA, Evans C J, Paquin R, Harris A & Jezzard P. Frequency and phase drift correction of magnetic resonance spectroscopy data by spectral registration in the time domain. Magn Reson Med. 2015;73(1):44–50.
  4. Tapper S, et al. Frequency and phase correction of J-difference edited MR spectra using deep learning. Magn Reson Med. 2021;85(4):1755–1765.
  5. Ma D J, et al. MR spectroscopy frequency and phase correction using convolutional neural networks. Magn Reson Med. 2022;87(4):1700–1710.
  6. Wang S, et al. DeepcomplexMRI: Exploiting deep residual network for fast parallel MR imaging with complex convolution. Magn Reson Imaging. 2020;68:136-147.
  7. Simpson R, Devenyi G A, Jezzard P, Hennessy T J & Near J. Advanced processing and simulation of MRS data using the FID appliance (FID-A)—An open source, MATLAB-based toolkit. Magn Reson Med. 2017;77(1):23–33.

Figures

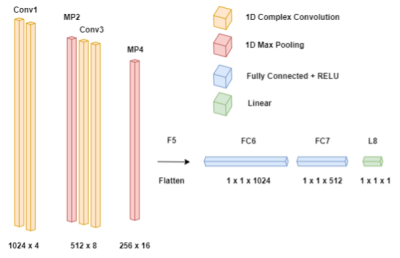
Figure 1: Proposed C-CNN model. The input to the pipeline consists of the complex spectral points of a single subspectra which pass through a frequency network, as seen above. The frequency shift prediction is then inversely applied to the spectral points for correction, passed through a phase network, identical in layer characteristics to the frequency network, and phase corrected. Subspectra (ON and OFF) are then subsequently subtracted to obtain a difference spectrum.

Figure 2: FPC pipeline for our model, complex-valued convolutional neural network. Data acquired in the time domain is converted into a frequency domain spectrum via Fourrier Transform for inputs into the frequency and phase prediction networks (Figure 1). Predicted shift corrections are applied on time domain data prior to proceeding in the pipeline.

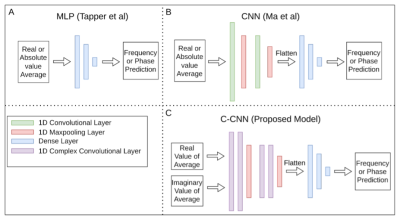
Figure 3: High-level view of network architectures of deep learning frequency and phase correction models. (A) Multi-layer perceptron (MLP) from Tapper et al. (B) Convolutional neural network (CNN) from Ma et al. (C) Our model, the complex-valued convolutional neural network (C-CNN).

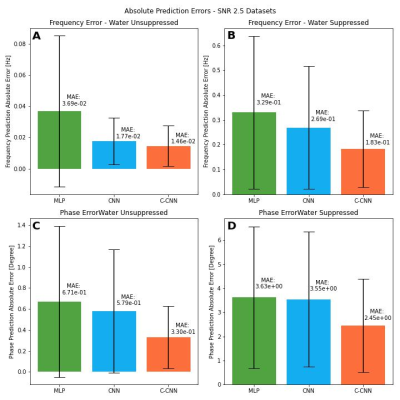
Figure 4: Comparative study comparing model performance on SNR 2.5 dataset calculated by the mean absolute error (|model predicted shift - ground truth applied shit|) where MLP is the model by Tapper et al., CNN is the most recent DL FPC model by Ma et al., and C-CNN is our model. (A) Frequency shift error for water unsuppressed data. (B) Frequency shift error for water suppressed data. (C) Phase shift error for water unsuppressed data. (D) Phase shift error for water suppressed data.

Proc. Intl. Soc. Mag. Reson. Med. 31 (2023)
0494
DOI: https://doi.org/10.58530/2023/0494