0473
Removal of Water and Lipid Signals from J-resolved 1H-MRSI Data Using an FID Reference and Physics-Based Subspaces1Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 2Department of Electrical and Computer Engineering, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 3National Center for Supercomputing Applications, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 4Siemens Medical Solutions USA, Inc., Urbana, IL, United States, 5School of Biomedical Engineering, Shanghai Jiao Tong University, Shanghai, China
Synopsis
Keywords: Data Processing, Spectroscopy
J-resolved 1H-MRSI provides a unique capability to quantify both brain neurotransmitters and metabolites. This paper presents a novel method to effectively remove water and lipid signals from J-resolved 1H-MRSI data with limited spatial encodings and without lipid suppression. The proposed method has been validated using data from a healthy subject and a brain tumor patient, producing impressive results.Introduction
Recently, a new J-resolved MRSI technique has been proposed for fast high-resolution mapping of brain metabolites and neurotransmitters using hybrid FID (free induction decay) and SE (spin echo) acquisitions1. The method achieves high imaging speed by sampling $$$(\boldsymbol{k},t,t_J)$$$-space “sparsely” in acquiring spatial, spectral, and J-evolution information. More specifically, in the accelerated data acquisition scheme, short-TR FID signals were acquired with extended k-space coverage to achieve high spatial resolution while long-TR SE signals (which encode both chemical shift and J-evolution spectral information) were acquired with limited k-space to reduce data acquisition time. One challenging problem with this fast data acquisition scheme is the removal of lipid and water signals from the SE data. Although several data processing methods have been proposed and used for removing water and lipid signals from 1H-MRSI data2-7, they are not adequate for solving the nuisance removal problem associated with fast J-resolved MRSI due to the very limited number of spatial encodings acquired without lipid suppression.In this work, we provided an effective solution to this problem using a physics-based subspace model to incorporate high-resolution FID reference spectroscopic data8. The proposed method has been validated using in vivo data acquired from healthy and brain tumor subjects, producing impressive results.
Methods
Using the hybrid data acquisition scheme1, the acquired J-resolved MRSI datasets include FID data, $$$d_{\text{FID}}(\boldsymbol{k},t,t_J),t_J=0$$$, with extended k-space coverage, and dual-echo SE data, $$$d_{\text{SE}}(\boldsymbol{k},t,t_J),t_J\in\{TE_1,TE_2\}$$$, with limited k-space coverage for two TEs (to encode J-evolution information), as illustrated in Fig. 1.To effectively leverage the high-resolution FID data for water and lipid removal from the SE data, we used a joint representation of the FID and SE MRSI signals with the following union-of-subspaces model8:
$$\hspace{27.5em}\rho(\boldsymbol{x},f,J)=\sum_{m=1}^{M}\sum_{\ell=1}^{L_m}{u_{m,\ell}(\boldsymbol{x})v_{m,\ell}(f,J)}, \hspace{27.5em}(1)$$
where $$$v_{m,\ell}(f,J)_{\ell=1}^{L_m}$$$ is a set of pre-determined spectral subspaces for the $$$m^{th}$$$molecule, e.g., water and lipid, and $$$u_{m,\ell}(\boldsymbol{x})_{\ell=1}^{L_m}$$$ a set of spatial coefficients shared by FID and SE data. The FID/SE-shared coefficients and learned spectral subspaces enabled the translation of high-resolution FID reference to SE data, which provided essential spatiospectral information for the reconstruction and removal of water and lipid signals from low-resolution SE data.
Determination of Water and Lipid Subspaces
To capture the inconsistencies between FID and SE data, we estimated FID/SE joint subspaces with physics prior information and training data. First, we used the following spectral model for water and lipid signals9:
$$\hspace{24.2em}\rho(t,J)=[c^\text{w}\phi^\text{w}(t,J)e^{-R_{2,\text{w}}^*t}+c^\text{f}\phi^\text{f}(t,J)e^{-R_{2,\text{f}}^*t}]h(t,J),\hspace{24.2em}(2)$$
where $$$c^\text{w}$$$ and $$$c^\text{f}$$$ denote the concentrations for water and lipids; $$$\phi^\text{w}(t,J)$$$ and $$$\phi^\text{f}(t,J)$$$ the resonance structures for water and lipids10 that capture the physical differences between the FID and SE signals; $$$R^*_{2,\text{w}}$$$ and $$$R^*_{2,\text{f}}$$$ the apparent relaxation constants; $$$h(t,J)$$$ the lineshape function that absorbs experimental variations between FID and SE signals, e.g., field drifts. The resonance structures were determined using quantum mechanical simulation and the Bloch equation, which reduced the learning complexity to determine the joint subspaces. Then the empirical distribution of spectral parameters, i.e., $$$c^\text{w},c^\text{f},R^*_{2,\text{w}},R^*_{2,\text{f}},h(t,J)$$$, were estimated from training data with high spatial resolution. With the estimated spectral parameters, a dictionary of synthetic FID and SE signals was generated using the signal model in Eq. (2), and their joint subspaces were extracted using singular value decomposition.
Estimation of Spatial Coefficients
With the pre-learned joint subspaces, we estimated the corresponding spatial coefficients from FID/SE imaging data by solving the following optimization problem:
$$\hspace{24.2em}\hat{U}=\text{arg}\min_U\left\lVert\begin{bmatrix}d_{\text{FID}}\\d_{\text{SE}_1}\\d_{\text{SE}_2}\end{bmatrix}-\begin{bmatrix}\Omega_{\text{FID}}FV_{\text{FID}}\\\Omega_{\text{SE}_1}FV_{\text{SE}_1}\\\Omega_{\text{SE}_2}FV_{\text{SE}_2} \end{bmatrix}U\right\rVert^2_2+R(U),\hspace{24.2em}(3)$$
where $$$d_{\text{FID}},d_{\text{SE}_1}$$$ and $$$d_{\text{SE}_2}$$$ denote the collected data, $$$U$$$ the high-resolution FID/SE shared spatial coefficients, $$$V_{\text{FID}},V_{\text{SE}_1}$$$ and $$$V_{\text{SE}_2}$$$ the pre-determined subspaces, $$$\Omega_{\text{FID}},\Omega_{\text{SE}_1}$$$ and $$$\Omega_{\text{SE}_2}$$$ the sampling operators, $$$F$$$ the Fourier operator, and $$$R(\cdot)$$$ the regularization functional. This optimization problem was solved using the conjugate gradient method. With the estimated spatial coefficients $$$\hat{U}$$$, the nuisance signals were reconstructed and removed from J-resolved 1H MRSI data. Finally, the neurotransmitters and metabolites signals were obtained from nuisance-removed hybrid FID/SE data using the union-of-subspaces model9,12.
Results
To validate the proposed method, J-resolved 1H-MRSI data were acquired from a healthy volunteer and a brain tumor patient on a 3T scanner (MAGNETOM Prisma, Siemens Healthcare, Erlangen, Germany) using the hybrid FID/SE acquisition scheme1.Figures 2 and 3 compared lipid and water removal results obtained by the proposed method, with FFT, Papoulis-Gerchberg (PG) algorithm (for lipid removal)2, HSVD algorithm (for water removal)4, and SE-only subspace-based nuisance removal method7. The results demonstrated that the proposed method achieved the most effective lipid and water removal among all methods.
Figure 4 shows the metabolite maps and spectra obtained in a test-retest experiment. As can be seen, high-resolution nuisance-free metabolic signals were reconstructed. Besides, the reconstructed maps and spectra were highly reproducible, indicating the good stability of the proposed method.
Figure 5 shows the results obtained from a brain tumor patient. Noticeable reduction in NAA and elevation in lactate were observed in the lesion, without contamination from nuisance signals.
Conclusions
We proposed a novel method to remove nuisance signals from J-resolved 1H-MRSI data acquired with limited spatial encodings and no lipid suppression. The proposed method was validated using in vivo data, producing highly reproducible nuisance-free metabolite maps. This new method may provide an effective and robust solution to the nuisance removal problem often associated with fast J-resolved 1H-MRSI of the brain.Acknowledgements
No acknowledgement found.References
1. Zhao Y, Li Y, Xiong J, Guo R, Li Y, Liang Z-P. Rapid high-resolution mapping of brain metabolites and neurotransmitters using hybrid FID/SE-J-resolved spectroscopic signals. In Proceedings of the 28th Annual Meeting of ISMRM, pp. 0366, 2020.2. Haupt C I, Schuff N, Weiner M W, et al. Removal of lipid artifacts in 1H spectroscopic imaging by data extrapolation. Magn Reson Med. 1998;35(5):678-687.
3. Ogg R, Kingsley R, Taylor J. WET, a T1- and B1-insensitive water-suppression method for in vivo localized 1H NMR spectroscopy. J Magn Reson Series B 1994; 104:1-10.
4. Barkhuisen H, de Beer R, van Ormondt D. Improved algorithm for noniterative time-domain model fitting to exponentially damped magnetic resonance signals. J Magn Reson 1987; 73:553-557.
5. Hernando D, Haldar J, Sutton B, Liang Z-P. Removal of lipid signal in MRSI using spatial-spectral constraints. In IEEE International Symposium on Biomedical Imaging, 2007;1360-1363.
6. Bilgic B, Gagoski B, Kok T, Adalsteinsson E. Lipid suppression in CSI with spatial priors and highly undersampled peripheral k-space. Magn Reson Med. 2013;69(6):1501-1511.
7. Ma C, Lam F, Johnson C L, Liang Z-P. Removal of nuisance signals from limited and sparse 1H MRSI data using a union-of-subspaces model. Magn Reson Med.2016;75(2):488-497.
8. Liang Z-P. Spatiotemporal imaging with partially separable functions. In: IEEE International Symposium on Biomedical Imaging, Arlington, VA, USA, 2007; pp. 988-991.
9. Lam F, Li Y, Guo R, Clifford B, Liang Z-P. Ultrafast magnetic resonance spectroscopic imaging using SPICE with learned subspaces. Magn Reson Med. 2020; 83: 377-390.
10. Peterson, P, Trinh, L, Månsson, S. Quantitative 1H MRI and MRS of fatty acid composition. Magn Reson Med. 2020; 85: 49-67.
11. Liang Z-P, Lauterbur PC. A generalized series approach to MR spectroscopic imaging. IEEE Trans Med Imaging. 1991;10(2):132-137.
12. Li Y, Lam F, Clifford B, Liang Z-P. A subspace approach to spectral quantification for MR spectroscopic imaging. IEEE Trans Biomed Eng. 2017;64(10):2486-2489.
Figures
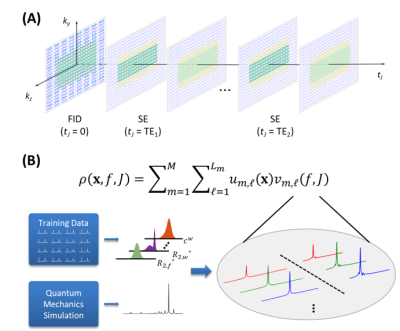
Figure 1. A schematic overview of the proposed method. (A) Hybrid FID/SE data acquisition scheme that acquires spatial, spectral, and J-coupling information. (B) Union-of-subspaces model for data processing. Note that in data acquisition, the FID data have extended k-space coverage while dual-echo SE data have limited k-space coverage; in data processing, physics-based joint subspaces with learned basis functions are used.
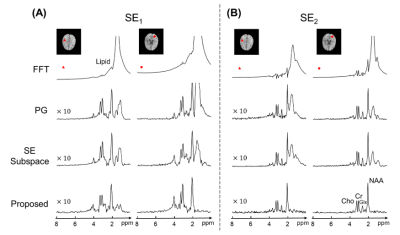
Figure 2. Comparison of lipid removal results for two representative voxels in SE1 data (A) and SE2 data (B). Spectra processed using Fourier reconstruction (FFT), Papoulis-Gerchberg algorithm (labeled as PG), SE-only subspace nuisance removal, and the proposed method were shown. Note that the proposed method produced high-quality metabolite and neurotransmitter spectra with negligible residual lipid signals.
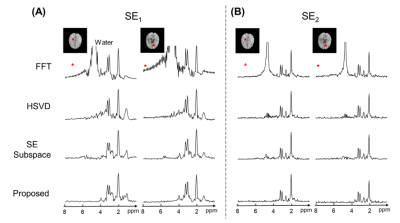
Figure 3. Comparison of water removal results for two representative voxels in SE1 data (A) and SE2 data (B). Spectra processed using Fourier reconstruction (FFT), HSVD, SE-only subspace nuisance removal, and the proposed method were shown. Note that the proposed method produced high-quality metabolite and neurotransmitter spectra with negligible residual water signals.
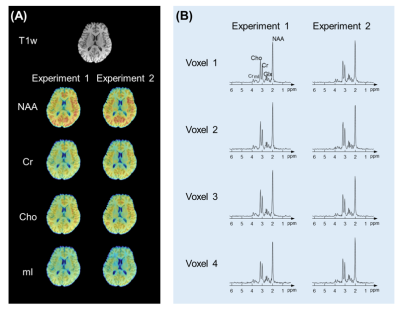
Figure 4. Reproducibility study results. (A) T1-weighted anatomical image and metabolite maps obtained in a test-retest experiment. (B) Representative localized spectra. Note that highly reproducible metabolite maps and spectra were obtained from both experiments without lipid or water residues.
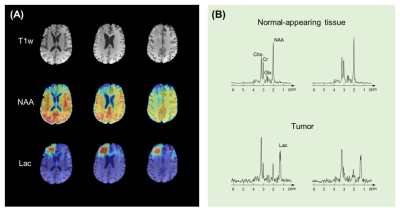
Figure 5. Tumor patient results. (A) T1-weighted anatomical image, NAA map, and Lac maps obtained from the patient. (B) Representative localized spectra in the normal-appearing tissue and tumor regions. Clear reduction in NAA and elevation in Lac were observed in the tumor, free of contamination from water and lipid signals.