Synopsis

Keywords: Data Analysis, MR Fingerprinting

Cramér-Rao Lower Bound has been used to optimize the acquisition design for MRF, but the effect from undersampling and reconstruction has not been taken into consideration. In this work, we evaluated the estimation error and standard deviation using CRLB optimized acquisition parameters with spiral undersampling trajectory and subspace reconstruction. The results demonstrated that CRLB produced lower estimation variation but is sensitive to the selected number of subspaces. A rank that is too low or two high an increase the estimation error. The dictionary match on coefficient maps provided lower estimation error and variation compared to match on whole time series.

Introduction

Magnetic resonance fingerprinting (MRF) has been a powerful quantitative imaging technique, achieving rapid high-quality multiparametric mapping for different organs and tissues^1-3. In recent years, Cramér-Rao Lower Bound (CRLB) has been applied to optimize the acquisition parameters for MRF including TR and flip angle trains to achieve increased SNR and reduced noise in the quantification^4-5. Theoretical evaluation has been performed, showing promising results with reduced standard deviation of estimated tissue parameters. However, these optimization works were performed based on Bloch equation with the assumption of independently and identically distributed (i.i.d) gaussian noise over the acquisition time points. In practice, the undersampling schemes and low-rank subspace based reconstruction⁶ will affect the geometry (g) -factor of the image, and thus alter the noise distribution spatially and temporally. The chosen number of subspaces can also affect the noise level of reconstructed images as well as the quantification of the parametric maps. In this work, we performed a comprehensive evaluation of the effect of CRLB optimization with undersampling and subspace reconstruction to optimize the MRF acquisition and reconstruction schemes.

Methods

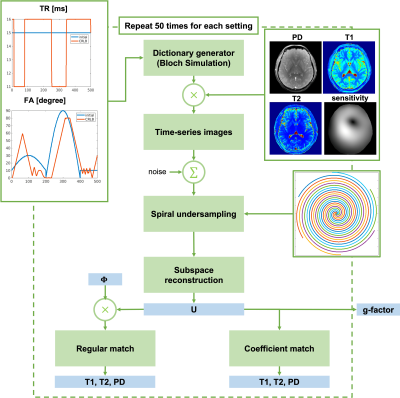
CRLB optimization for acquisition parameters: The TR and flip angle trains were optimized using the efficient CRLB optimization framework based on automatic differentiation⁵. A realistic set of TR and flip angles from recent work³ was used as an initialization. Each repetition consisted of 500 TRs. The range of TRs to be optimized is 11 ms to 16 ms, and the range of flip angles is 0-90°.
Image generations: As shown in Figure 1, a set of proton density (PD), T1, and T2, and coil sensitivity maps from a 1-mm iso 2D fully sampled MRF study were served as ground truth. Two sets of multi-coil time-series images were generated. One is using the dictionary with initial parameters, and the other is using the dictionary with CRLB-optimized parameters. The i.i.d. Gaussian noise was added independently to each time frame and the averaged SNR was 40.
Undersampling trajectories: A 2D variable-density spiral trajectory was implemented in this study. The undersampling rate is 24 at the center k-space, and 48 at outer k-space. The spiral readout is 6.1 ms.
Subspace reconstruction: Low-rank subspace reconstruction was performed to exploit the high spatiotemporal correlation of MRF image across time points^3,6. The reconstruction can be formulated as$$\widehat{\mathbf{U}}=\arg\min_{\mathbf{U}}\|\mathbf{{\Omega}FS}\mathbf{U}\boldsymbol{\Phi}-\mathbf{d}\|_{2}^{2}+R(\mathbf{U}),$$where $$$\mathbf{d}$$$ is the acquired data, $$$\Omega$$$ is the spiral undersampling trajectory, $$$\mathbf{F}$$$ is Fourier transform, $$$\mathbf{S}$$$ is coil sensitivity, $$$\boldsymbol{\Phi}$$$ is temporal subspace pre-determined from the dictionary using initial or CRLB-optimized acquisition parameters, and $$$\boldsymbol{U}$$$ is the spatial coefficient to be solved. Only linear reconstruction is used to maintain the noise distribution. In the reconstruction, the number of subspaces L was evaluated from 4 to 8.
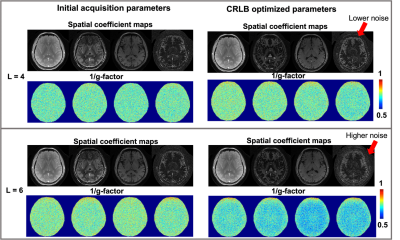
g-Factor evaluation: The g-factors of the spatial coefficient $$$\boldsymbol{U}$$$ were evaluated for images with different acquisition parameters (initial or CRLB optimized) and different ranks . A pseudo multi-replica approach was implemented for g-factor calculation⁷. For each combination of acquisition parameters and , the entire simulation experiment was repeated 50 times with different noise.
Dictionary match: The regular template matching was performed between the dictionary and reconstructed time-series images. However, with subspace recon, the rank of the time-series images is reduced to L, and the images across time points are not independent. To account for the correlation along timepoints, a template match was performed between the coefficient maps and the compressed dictionary by applying the Hermitian conjugate of temporal subspaces $$$\boldsymbol{\Phi}$$$ on to the dictionary. The compression significantly reduced the size of the dictionary as well as the time for matching. The mapping result with regular match or coefficient match were both evaluated.

Results

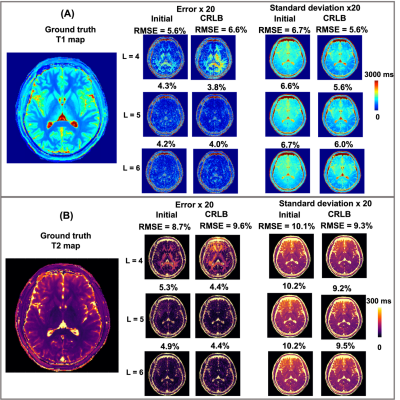
Figure 2 shows the 1/g-factor maps for each coefficient map for L = 4 and 6. With the increase of L, the 1/g-factor decreases significantly for CRLB set, indicating a reduced SNR due to increased spatiotemporal separability and reduced correlation.
Figure 3 displays the error maps and standard deviation of T1 estimation using regular dictionary matching for both acquisition parameters. CRLB-optimized group showed consistently lower standard deviation in the estimation, but increased error when L is low (L=4).
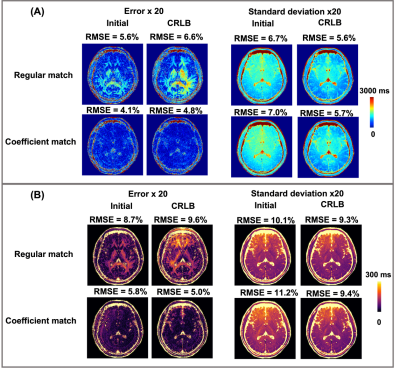
Figure 4 illustrates the performance of regular dictionary match on all time points and compressed match on spatial coefficients. When L=4, the regular match showed substantial error for both T1 and T2, while the coefficient match can significantly decrease the estimation error and the standard deviation.
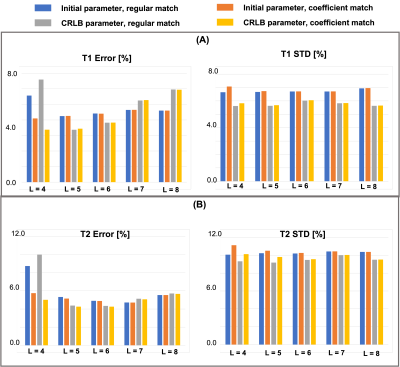
The bar graph in Figure 5 demonstrates the estimated error and standard deviation for T1 and T2 at different L for both acquisition parameters. CRLB optimized acquisition parameters showed reduced standard deviation in all cases compared to initial acquisition, but can result in higher error when L is too low or too high. The coefficient match consistently produced smaller error and standard deviation.

Conclusion

The CRLB optimization is able to reduce the variation of the parameter estimation for MRF with undersampling and subspace reconstruction. A careful selection of the number of subspaces will improve the estimation accuracy. Dictionary match on coefficient maps reduces estimation error and variation. Future works to optimize both the acquisition parameters together with the undersampling and reconstruction is necessary.

Acknowledgements

No acknowledgement found.