0427
Improved Low-Rank and Subspace Reconstruction for Magnetic Resonance Fingerprinting with Self-Navigating Acquisitions1Department of Biomedical Engineering, University of Texas at Austin, Austin, TX, United States, 2State Key Laboratory of Modern Optical Instrumentation, College of Optical Science and Engineering, Zhejiang University, Hangzhou, China, 3Center for Brain Imaging Science and Technology, Key Laboratory for Biomedical Engineering of Ministry of Education, College of Biomedical Engineering and Instrumental Science, Zhejiang University, Hangzhou, China, 4Oden Institute for Computational Engineering and Sciences, University of Texas at Austin, Austin, TX, United States
Synopsis
Keywords: Quantitative Imaging, MR Fingerprinting
Low-rank and subspace reconstruction methods have achieved state-of-the-art performance for MR Fingerprinting with highly-undersampled data. The existing methods learn the temporal subspace from an ensemble of magnetization evolutions generated from Bloch simulations. In this work, we present a novel self-navigating acquisition scheme for MR Fingerprinting, which utilizes a dual-echo acquisition strategy to enable subspace estimation from physically-acquired training data. The proposed acquisition substantially improves the accuracy of the low-rank and subspace reconstruction, especially when the acquisition length is short. We demonstrate the performance of the proposed method with phantom experiments and in vivo experiments.Introduction
Magnetic resonance fingerprinting1 (MRF) is a transient-state quantitative MRI technique that enables the simultaneous quantification of multiple MR tissue parameters (e.g., T1, T2, and proton density) in a single imaging experiment. It has demonstrated promising results for various applications2–7. The original MRF employs a simple dictionary matching reconstruction1, which is often computationally efficient. However, its accuracy often dramatically degrades as the acquisition length becomes short. Over the past few years, various model-based and/or data-driven reconstruction methods8-16 have been developed to improve the accuracy of MRF. As a state-of-the-art method, low-rank reconstruction11-13 exploits the strong correlation of MRF time-series images and further learns the temporal subspace of the model from simulated magnetization evolutions. Here the accuracy of subspace estimation often plays a key role in the times-series image reconstruction and subsequent tissue parameter quantification.In this work, we introduce a novel MRF acquisition scheme for low-rank and subspace reconstruction. It employs a dual-echo self-navigating strategy to enable improved subspace estimation with physically-acquired training data, while maintaining the same acquisition time. It substantially improves the accuracy of the low-rank and subspace reconstruction, especially when the acquisition length is short. We demonstrate the performance of the proposed method with phantom experiments and in vivo experiments.
Methods
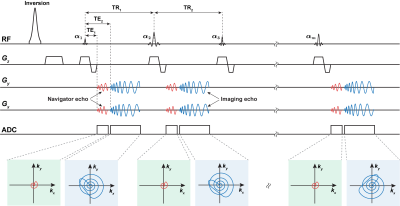
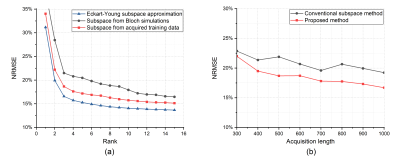
The low-rank and subspace reconstruction exploits the strong correlation of MRF time-series images by imposing a low-rank model, i.e., $$$\text{rank}(\mathbf{C}) \leq L$$$, on the following Casorati matrix10-13 $$\mathbf{C}=\left[\begin{array}{ccc}I\left(r_1, t_1\right) & \cdots & I\left(r_1, t_M\right) \\\vdots & \ddots & \vdots \\I\left(r_N, t_1\right) & \cdots & I\left(r_N, t_M\right)\end{array}\right] \in \mathbb{C}^{N \times M}.$$ Mathematically, the low-rank constraint can be enforced explicitly via matrix factorization $$$\mathbf{C=UV}$$$, where $$$\mathbf{U} \in \mathbb{C}^{N \times L}$$$ and $$$\mathbf{V} \in \mathbb{C}^{L \times M}$$$ correspond to the spatial and temporal subspaces, respectively. A subspace constraint can be further incorporated by assuming the temporal subspace $$$\mathbf{V}$$$ is known11-12. Accordingly, the time-series image reconstruction problem can be formulated as$$\hat{\mathbf{U}}=\arg \min _{\mathbf{U}} \sum_{{c}=1}^{{N}_{{c}}}\left\|\mathbf{d}_{\mathrm{c}}-\Omega\left(\mathbf{F S}_{{c}} \mathbf{U} \hat{\mathbf{V}}\right)\right\|_2^2$$ where $$$\mathbf{d}_{c} $$$ contains the measured data from the cth coil, $$$\mathbf{F} $$$ denotes the Fourier encoding matrix, $$$\mathbf{S}_{c} $$$ is the coil sensitivity matrix, and $$$\hat{\mathbf{V}}$$$ is a pre-estimated temporal subspace, and $$$\Omega(\cdot)$$$ is an imaging operator modeling the acquisition process. The existing low-rank and subspace reconstruction learns $$$\hat{\mathbf{V}}$$$ from magnetization evolutions simulated from Bloch simulations using the principal component analysis11-12. Note that various factors, including the range of tissue parameters, tissue models (e.g., multi-compartment model), and acquisition imperfections (e.g., slice profiles), need to be properly modeled in Bloch simulations. Any subspace estimation error could degrade the image reconstruction and quantification of MR tissue parameters.Instead of estimating the subspace from simulated data, here we introduce a novel data acquisition scheme to enable subspace learning from physically-acquired training data. As illustrated in Figure 1, the proposed acquisition method features a dual-echo acquisition strategy, which acquires both a navigator echo and an imaging echo in each repetition time (TR). Here the navigator echoes are associated with the same k-space locations, which are significantly shorter than the imaging echoes. Thus the temporal subspaces from the navigator data are approximately the same as those from the imaging data. With short navigator echoes, we can also adopt the same TRs as the existing MRF acquisition. As illustrated in Figure 2 for an in vivo MRF scan described below, with subject-specific training data, we can substantially improve subspace estimation.
We evaluated the proposed method with phantom experiments and in vivo experiments on three healthy subjects on a 3T Siemens Prisma scanner with 20 receiver coils. Specifically, the proposed acquisition used TE1 = 2.11 ms for the navigator echoes and TE2 = 2.5 ms for the imaging echoes for all the TRs. In addition, it used the same FA and TR sequences and k-space trajectories for imaging data as in the IR-FISP MRF sequence17. For the acquisition of navigator data, we used a zero-order gradient moment compensation to avoid phase dispersion. Here the proposed acquisition achieves the same acquisition time as the original IR-FISP MRF acquisition, while allowing the use of auxiliary navigator data for subspace learning. Other related parameters include: FOV = 300×300 mm2, matrix size = 256×256, and slice thickness = 5 mm. Finally, we also acquired fully-sampled MRF data as our references to assess the performance of the proposed method.
Results
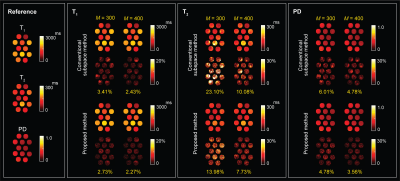
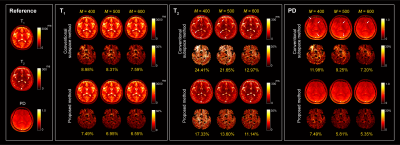
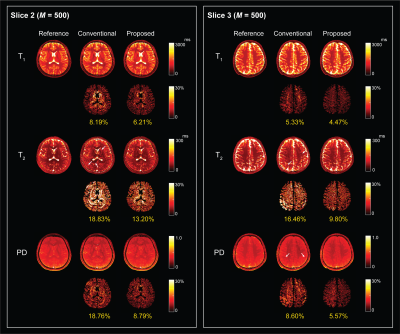
Figure 3 shows the reconstructed T1, T2, and proton density (PD) maps for the phantom experiments at two acquisition lengths, which illustrates the benefits of using physically-acquired training data for subspace estimation. Figure 4 shows the reconstructed tissue parameter maps for one subject in the in vivo experiment. Clearly, the proposed acquisition improves the low-rank and subspace reconstruction for all the tissue parameters both quantitatively and quantitatively. Here the improvement are more significant for the T2 and PD maps. Figure 5 shows the reconstructed tissue parameter maps for the other two subjects, which consistently demonstrates the improvement of the proposed method.Conclusion
We presented a new MRF acquisition method for the low-rank and subspace reconstruction. It employs a dual-echo self-navigating acquisition scheme to acquire training data for improved subspace estimation while maintaining the same acquisition time. The phantom and in vivo experiments demonstrate that it significantly improves the accuracy of the state-of-the-art low-rank reconstruction.Acknowledgements
This project was partially supported by the National Institutes of Health.References
[1] D. Ma, V. Gulani, N. Seiberlich, K. Liu, J. L. Sunshine, J. L. Duerk, and M. A. Griswold, "Magnetic resonance fingerprinting," Nature, vol. 495, pp. 187-192, 2013.
[2] M. A. Cloos, F. Knoll, T. Zhao, K. T. Block, M. Bruno, G. C. Wiggins and D. K. Sodickson, "Multiparametric imaging with heterogeneous radiofrequency fields," Nat. Commun., vol. 7, 12445, 2016.
[3] Y. Chen, Y. Jiang, S. Pahwa, D. Ma, L. Lu, M. D. Twieg, K. L. Wright, N. Seiberlich, and M. A. Griswold, and V. Gulani, "MR fingerprinting for rapid quantitative abdominal imaging," Radiology, vol. 279, pp. 278-286, 2016.
[4] J. I. Hamilton, Y. Jiang, Y. Chen, D. Ma, W.-C. Lo, and M. A. Griswold, and N. Seiberlich, "MR fingerprinting for rapid quantification of myocardial T1, T2, and proton spin density," Magn. Reson. Med., vol. 77, pp. 1446-1458, 2017.
[5] C. Liao, K. Wang, X. Cao, Y. Li, D. Wu, H. Ye, Q. Ding, H. He, and J. Zhong, "Detection of lesions in mesial temporal lobe epilepsy by using MR fingerprinting," Radiology, vol. 3, pp. 804-812, 2018.
[6] A. Sharafi, M. Zibetti, G. Chang, M. Cloos, and R. R. Regatte, "MR fingerprinting for rapid simultaneous T1, T2, and T1ρ relaxation mapping of the human articular cartilage at 3T," Magn. Reson. Med., vol. 84, pp. 2636-2644, 2020.
[7] O. Cohen, V. Yu, K. Tringale, R. J. Young, O. Perlman, C. T. Farrar, and R. Otazo, "CEST MR fingerprinting (CEST-MRF) for brain tumor quantification using EPI readout and deep learning reconstruction," Magn. Reson. Med., vol. 89, pp. 233-249, 2023.
[8] E. Y. Pierre, D. Ma, Y. Chen, C. Badve, and M. A. Griswold, "Multiscale reconstruction for MR fingerprinting," Magn. Reson. Med., vol. 75, pp. 2481 - 2492, 2016.
[9] B. Zhao, K. Setsompop, H. Ye, S. F. Cauley, and L. L. Wald, "Maximum likelihood reconstruction for magnetic resonance fingerprinting," IEEE Trans. Med. Imaging, vol. 35, pp. 1812-1823, 2016.
[10] M. Doneva, T. Amthor, P. Koken, K. Sommer, and P. Börnert, "Matrix completion-based reconstruction for undersampled magnetic resonance fingerprinting data," Magn Reson Imaging., vol. 41, pp. 41-52, 2017.
[11] B. Zhao, K. Setsompop, E. Adalsteinsson, B. Gagoski, H. Ye, D. Ma, Y. Jiang, P. Ellen Grant, M. A. Griswold, and L. L. Wald, "Improved magnetic resonance fingerprinting reconstruction with low-rank and subspace modeling," Magn. Reson. Med. vol. 79, pp. 933-942, 2018.
[12] J. Assländer, M. A. Cloos, F. Knoll, D. K. Sodickson, J. Hennig, and R. Lattanzi, "Low rank alternating direction method of multipliers reconstruction for MR fingerprinting," Magn. Reson. Med., vol. 79, pp. 83-96, 2018.
[13] G. Lima da Cruz, A. Bustin, O. Jaubert, T. Schneider, R. M. Botnar, and C. Prieto, "Sparsity and locally low rank regularization for MR fingerprinting," Magn. Reson. Med., vol. 81, pp. 3530-3543, 2019.
[14] Z. Fang, Y. Chen, M. Liu, L. Xiang, Q. Zhang, Q. Wang, W. Lin, and D. Shen, "Deep learning for fast and spatially constrained tissue quantification from highly accelerated data in magnetic resonance fingerprinting," IEEE Trans. Med. Imaging, vol. 38, pp. 2364-2374, 2019.
[15]
Y. Chen, Z. Fang, S.-C. Hung, W.-T. Chang, D. Shen, and W. Lin, "High-resolution 3D MR Fingerprinting using parallel imaging and deep learning,"
Neuroimage, vol. 206, pp. 116329, 2020.
[16] F. Balsiger, A. Jungo, O. Scheidegger, P. G. Carlier, M. Reyes,
and B. Marty, "Spatially regularized parametric map reconstruction for
fast magnetic resonance fingerprinting," Med. Image Anal., vol. 64, 101741, 2020.
[17] Y. Jiang, D. Ma, N. Seiberlich, V. Gulani, and M. A. Griswold, "MR fingerprinting using fast imaging with steady state precession (FISP) with spiral readout," Magn. Reson. Med, vol. 74, pp. 1621-1631, 2015.
Figures