0423

Semi-Supervision for Clinical Contrast-Weighted Image Synthesis from Magnetic Resonance Fingerprinting

Mahmut Yurt¹, Cagan Alkan¹, Sophie Schauman^1,2, Xiaozhi Cao^1,2, Congyu Liao^1,2, Siddharth Iyer^1,3, Tolga Cukur⁴, Shreyas Vasanawala², John Pauly¹, and Kawin Setsompop^1,2
¹Department of Electrical Engineering, Stanford University, Stanford, CA, United States, ²Department of Radiology, Stanford University, Stanford, CA, United States, ³Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA, United States, ⁴Department of Electrical Engineering, Bilkent University, Ankara, Turkey

Synopsis

Keywords: MR Fingerprinting/Synthetic MR, MR Fingerprinting

Previous works have introduced deep models to synthesize clinical contrast-weighted images from magnetic resonance fingerprinting (MRF). Although these models achieve high synthesis accuracy, they demand full-supervision from fully-sampled training data of clinical contrasts which might become difficult to acquire across diverse sets due to scan costs. To eliminate undesirable reliance on full-supervision, we introduce a semi-supervised model, ssMRF, that allows training using accelerated references. ssMRF introduces a semi-supervised loss function based only on collected k-space samples of clinical contrasts, and further leverages complementary Poisson disc masks, via a multi-task learning protocol to synergistically synthesize multiple contrasts.

Introduction

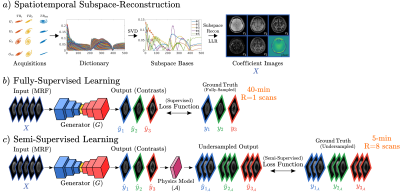
Recent advances in magnetic resonance fingerprinting (MRF) ¹¹ based on sequence-design innovations ^1,10,12 and subspace-reconstruction ^1,4-6 have enabled high-resolution whole-brain protocols for quantification of multi-tissue parameters in just a few minutes ^2,7. While tissue quantification has potential in clinical applications, radiologists often require traditional contrast-weighted images for diagnosis ⁸. Unlike MRF acquisition, contrast-weighted exams can take ~20-40 minutes. Natural approach to bypass prolonged contrast scans is to employ MR-physics synthesis (Bloch-equations) of contrast-weighted images from MRF-generated quantitative maps. However, this suffers from incomplete acquisition modeling, and magnetization transfer effect could be difficult to estimate ¹³. Therefore, several studies have developed data-driven models that learn to synthesize contrast-weighted images from MRF ^{8, 9,13,14}. Although these models demonstrate success, they relied on full-supervision from ground-truth contrasts, demanding training sets of paired, high-quality MRF and lengthy contrast-weighted scans. Note that compiling such datasets becomes impractical even for training purposes, particularly across diverse clinical populations needed to ensure robust training ^17-19.

To address this limitation, we propose a semi-supervised model (ssMRF) that introduces a training framework with highly-accelerated acquisitions of clinical contrasts, reducing scan-time requirements for training data. Contrary to previous fully-supervised models that define loss on entire k-space of contrasts, ssMRF leverages a semi-supervised loss based only on acquired k-space points of accelerated acquisitions, via physics-guidance. For homogenous learning across k-space, ssMRF further utilizes complementary Poisson disc masks across distinct training subjects/contrasts, via multi-task learning to synergistically synthesize multi-contrasts.

Methods

Semi-Supervised Synthesis: ssMRF (Fig. 1) involves a multi-task transformer-generator ¹⁶ $$$G$$$ that jointly synthesizes multiple clinical contrasts $$$\hat{Y}=\{\hat{y_1},\hat{y_2},\dots,\hat{y_n}\}$$$ from MRF subspace coefficient images $$$X$$$, such that, $$$G(X)=\hat{Y}$$$. Since ground-truth contrasts used here for training come from accelerated acquisitions, corresponding images suffer from aliasing artifacts that prohibit use of supervised loss functions. Therefore, ssMRF utilizes a physics-guidance module $$$\mathcal{A}$$$ to generate synthesized undersampled multi-coil counterparts, such that, $$$\hat{Y}_\mathcal{A}=\mathcal{A}(G(X))=\mathcal{F}^{-1}P_Y\mathcal{F}C_YG(X)$$$, where $$$\hat{Y}_\mathcal{A}$$$ denotes synthesized undersampled multi-coil images, $$$C_Y$$$ denotes coils, $$$P_Y$$$ denotes undersampling masks, and $$$\mathcal{F}$$$-$$$\mathcal{F}^{-1}$$$ denote forward-inverse Fourier transforms.

Accordingly, we define the semi-supervised loss in terms of k-space, image, and adversarial domains between synthesized and reference undersampled multi-coil images.

Fourier-Domain Loss: A k-space cost between synthesized and reference target images is enforced on acquired coefficients:$$L_{F}=\mathbb{E}_{X,Y}[||\mathcal{F}\left(\mathcal{A}G(X))-\mathcal{F}(Y\right))||_1]$$
Image-Domain Loss: Network robustness is improved via cost between image-domain data of synthesized and reference acquisitions:$$L_{I}=\mathbb{E}_{X,Y}[||\mathcal{A}G(X)-Y||_1]$$
Adversarial-Domain Loss: Level of realism in synthesis is enhanced via a discriminator on undersampled synthesized and reference images:$$L_{A}=-\mathbb{E}_Y[((D(Y)-1)^2)]-\mathbb{E}_{X}[D(\mathcal{A}G(X)) ]$$ where discriminator $$$D$$$ distinguishes between synthesized and reference accelerated acquisitions.

These sub-loss functions are combined to form the final objective function in a min-max game between the generator and discriminator:$$\min_G\max_D\{ \lambda_{F}L_{F}+\lambda_{I}L_{I}+\lambda_{A}L_{A}\}$$

Data: We collected a dataset of MRF and clinical contrasts (T1-MPRAGE, T1-Cube, T2-Cube, FLAIR-Cube, DIR-Cube) at 3T from 12 healthy volunteers, with 8 training, 2 validation, 2 test subjects. MRF data were acquired using the 3D-TGAS-SPI ¹ scheme with 48 groups, yielding acquisition time of 5:57 minutes per subject. Fingerprinting dictionary was generated via extended phase graph using sequence parameters, and MRF acquisitions were reconstructed via locally-low-rank spatiotemporal subspace modeling and multi-frequency-interpolation $$$B_0$$$-inhomogeneity correction to recover coefficient maps. Contrast-weighted images were acquired via clinically-used MRPAGE and Cube sequences with 40 minutes total acquisition/subject, denoted as fully-sampled acquisitions. These data were retrospective undersampled to generate training data for ssMRF. Note, prospective R=8 acceleration data for ssMRF would have taken 5 minutes; manageable to insert at patient exams to allow large training data collection. MRF and contrast data were spatially registered via ¹⁵.

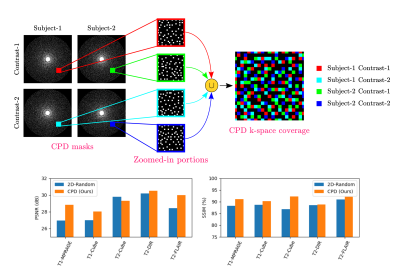
Mask Design: We leveraged complementary Poisson disc (CPD) sampling ²⁰(Fig. 2). CPD extends two-dimensional Poisson disc sampling to temporal dimension, and enforces complementariness such that same k-space points are not acquired across multiple time-frames. Here, we treated sampling masks for different subjects/contrasts as masks from time points in CPD. Accordingly, a unique variable density Poisson mask with calibration region was used for each contrast and subject. Having a calibration region in masks is critical as most energy in k-space lies in low-frequency regions; providing this information to synthesis network better conditions the problem. Also, complementary nature of sampling masks allows homogenous learning across k-space since different k-space points from different subjects/contrasts contribute to overall semi-supervised loss.

Results

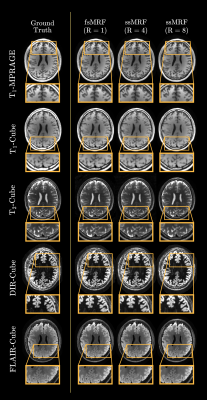
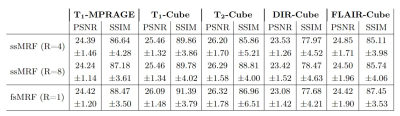
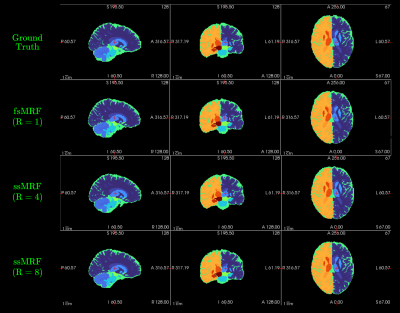
We trained two independent ssMRF models using clinical contrast accelerations of R={4,8}, denoted ssMRF(R=4) and ssMRF(R=8). We then compared them against a fully-supervised benchmark fsMRF(R=1). Note that fsMRF was trained using fully-sampled acquisitions of clinical contrasts, whereas ssMRF did not have access to full k-space data during training. Representative synthesized images are displayed in Fig.3, and PSNR-SSIM measurements between synthesized and ground-truth images in the test set are reported in Fig. 4. Reported measurements and images denote that proposed ssMRF models yield equivalent performance with benchmark fsMRF model, despite being trained on accelerated acquisitions with missing k-space samples. Representative segmentation maps based on synthesized images displayed in Fig. 5 also validate that proposed ssMRF model yields equivalent performance compared to fsMRF in such a downstream image analysis task.

Discussion

Here, we proposed a semi-supervised model for MRF-to-contrast synthesis. Continuing work focuses on developing prospectively undersampled scans for clinical use and utilization of zero-shot learning strategies for data-consistent inference time feedback-loop on the scanner.

Acknowledgements

This work was supported in part by NIH research grants: U01-EB029427, R01-EB009690, R01-EB020613, R01-EB019437, R01-MH116173, P41EB030006, and U01-EB025162, and GE Healthcare.

References

1. Cao X, Liao C, Srinivasan S, et al. Optimized multi-axis spiral projection MRF with subspace reconstruction for rapid 1-mm isotropic whole-brain MRF in 2 minutes. In: Proc. Intl. Soc. Mag. Reson. Med. ; 2021.

2. Schauman S.S., Iyer, S, Yurt, M, Cao, X, Liao, C, Zhong, Z, Wang, G, Zaharchuk, G, Vasanawala, S, Setsompop, K, “Toward a 1-minute high-resolution brain exam - MR Fingerprinting with fast reconstruction and ML-synthesized contrasts“ 2022 ISMRM Annual Meeting, London, UK

3. Iyer SS, Liao C, Li Q, et al. PhysiCal: A rapid calibration scan for B0, B1+, coil sensitivity and Eddy current mapping. In: Proc. Intl. Soc. Mag. Reson. Med. ; 2020. p. 661

4. Liang Z. Spatiotemporal imaging with partially separable functions. In: 2007 4th IEEE International Symposium on Biomedical Imaging: From Nano to Macro. Arlington, VA, USA: IEEE; 2007. pp. 988–991. doi: 10.1109/ISBI.2007.357020.

5. Zhao B, Setsompop K, Adalsteinsson E, et al. Improved magnetic resonance fingerprinting reconstruction with low-rank and subspace modeling: A Subspace Approach to Improved MRF Reconstruction. Magn. Reson. Med. 2018;79:933–942 doi: 10.1002/mrm.26701.

6. Assländer J, Cloos MA, Knoll F, Sodickson DK, Hennig J, Lattanzi R. Low rank alternating direction method of multipliers reconstruction for MR fingerprinting: Low Rank ADMM Reconstruction. Magn. Reson. Med 2018;79:83–96 doi: 10.1002/mrm.26639.

7. Gómez PA, Cencini M, Golbabaee M, et al. Rapid three-dimensional multiparametric MRI with quantitative transient-state imaging. Sci Rep 2020;10:13769 doi: 10.1038/s41598-020-70789-2.

8. Wang K, Doneva M, Amthor T, et al. High Fidelity Direct-Contrast Synthesis from Magnetic Resonance Fingerprinting in Diagnostic Imaging. In: Proc. Intl. Soc. Mag. Reson. Med. ; 2020. p. 867.

9. Qiu S, Chen Y, Ma S, et al. Direct Synthesis of Multi-Contrast Images from MR Multitasking Spatial Factors Using Deep Learning. In: Proc. Intl. Soc. Mag. Reson. Med. 29. ; 2021. p. 2429.

10. Cao X, Ye H, Liao C, Li Q, He H, Zhong J. Fast 3D brain MR fingerprinting based on multi‐axis spiral projection trajectory. Magn Reson Med 2019;82:289–301 doi: 10.1002/mrm.27726.

11. Ma D, Gulani V, Seiberlich N, et al. Magnetic resonance fingerprinting. Nature 2013;495:187–192 doi: 10.1038/nature11971.

12. Cao X, Liao C, Iyer SS, et al. Optimized multi-axis spiral projection MR fingerprinting with subspace reconstruction for rapid whole-brain high-isotropic-resolution quantitative imaging. arXiv:2108.05985 [physics] 2021.

13. Wang G, Gong E, Banerjee S, et al. Synthesize High-Quality Multi-Contrast Magnetic Resonance Imaging From Multi-Echo Acquisition Using Multi-Task Deep Generative Model. IEEE Trans. Med. Imaging 2020;39:3089–3099 doi: 10.1109/TMI.2020.2987026.

14. Tanenbaum LN, Tsiouris AJ, Johnson AN, et al. Synthetic MRI for Clinical Neuroimaging: Results of the Magnetic Resonance Image Compilation (MAGiC) Prospective, Multicenter, Multireader Trial. AJNR Am J Neuroradiol 2017;38:1103–1110 doi: 10.3174/ajnr.A5227.

15. Jenkinson M, Bannister P, Brady M, Smith S. Improved Optimization for the Robust and Accurate Linear Registration and Motion Correction of Brain Images. NeuroImage 2002;17:825–841 doi: 10.1006/nimg.2002.1132.

16. Dalmaz O, Yurt M, Cukur T. ResViT: Residual Vision Transformers for MultiModal Medical Image Synthesis. IEEE TMI 2022; 3167808

17. Yurt M, Dalmaz O, Dat S, et al. Semi-Supervised Learning of MRI Synthesis without Fully-Sampled Ground-Truths

18. Yaman B, Hosseini S, Moeller S. et al. Self-Supervised Physics-Based Deep Learning MRI Reconstruction Without Fully-Sampled Data. IEEE ISBI 2022.

19. Yaman B, Hosseini S, Akcakaya M. Zero-Shot Self-Supervised Learning for MRI Reconstruction. International Conference on Learning Representations 2022.

20. Levine E, Daniel B, Vasanawala S. 3D Cartesian MRI with Compressed Sensing and Variable View Sharing Using Complementary Poisson-disc Sampling. Magnetic Resonance in Medicine 2016;10.1002

Figures

Fig. 1) a) Raw MRF acquisitions are subspace reconstructed to form subspace coefficient images which are input to network models. b) Prior fully-supervised models use fully-sampled contrast-weighted images as ground-truth during training to learn a generator that maps MRF coefficient maps to clinical contrasts. c) The proposed semi-supervised model leverages a physics module to mimic acquisition protocol of reference accelerated acquisitions, in order to enable learning with missing k-space samples.

Fig. 2) Undersampling masks across different subjects and contrasts are obtained from complementary Poisson disc (CPD) masks. CPD masks ensure extended k-space coverage when individual masks for distinct subject/contrast combinations are unified. Also, see below for quantitative measurements for models trained with CPD masks versus 2D-random masks for accelerated contrast ground-truths of R=8. Overall, CPD masks yield improved PSNR and SSIM measurements compared to 2D-random masks across different target contrasts.

Fig. 3) Representative synthesis results are displayed from the proposed ssMRF and benchmark fully-supervised fsMRF models together with reference fully-sampled target images. Overall, the proposed ssMRF model yields equivalent performance to benchmark fully-supervised fsMRF model, although being trained with 8-fold accelerated acquisitions. Please see zoomed-in portions for details.

Fig. 4) Quantitative image quality metrics are reported in terms of PSNR and SSIM between synthesized and reference images to compare ssMRF (R=4,8) and fsMRF (R=1) for the five clinical contrasts in the dataset. Reported measurements denote that the proposed semi-supervised ssMRF model yields equivalent performance with the benchmark fully-supervised fsMRF model, although ssMRF was trained on accelerated acquisitions with missing k-space samples.

Fig. 5) Synthesized images from the fully-supervised and semi-supervised models were subjected to FreeSurfer segmentation together with the fully-sampled reference images. Segmentation maps displayed here demonstrate that the synthesis accuracy of the semi-supervised model is sufficient enough to obtain similar segmentation maps with the fully-supervised fsMRF model as well as fully-sampled references.

Proc. Intl. Soc. Mag. Reson. Med. 31 (2023)

0423

DOI: https://doi.org/10.58530/2023/0423