0392
An end-to-end residual learning VarNet for under-sampled MRI reconstruction1Research and Development Center, Canon Medical Systems (China), Beijing, China
Synopsis
Keywords: Machine Learning/Artificial Intelligence, Image Reconstruction
Model driven deep learning reconstruction methods usually utilize residual learning within single cascade which is composed by a neural network and a data consistency module, here we propose a model based end-to-end residual learning variational network(E2E-ResVarNet), a k-space residual is passed through cascades, then added to acquired under-sampled k-space after the last cascade output. It was demonstrated that the image quality is significantly improved at 4x/6x/8x acceleration factors trained with brain data set.
Introduction
Model driven deep learning reconstruction methods become popular because less training data is required compared with data-driven deep learning methods1. Model driven DL network consists of several cascades, each cascade includes a regularization neural network and a data consistency (DC) module2,3,4. To achieve better reconstruction performance, residual learning strategy is usually used within single cascade3,4,5. To our knowledge, there is no research to explorer end-to-end residual learning in model driven methods. In this study, we propose a model based end-to-end residual learning variational network, which is called E2E-ResVarNet, and demonstrated its superiority to non-end-to-end residual learning network.Method
Network design:The inverse problem of MRI reconstruction with deep learning network regularization can be formulated as:$$ \hat{x} = {argmin}_{x}\frac{1}{2}{\sum{\parallel M\mathcal{F}\left( {S_{i}x} \right) - {\overset{\sim}{k}}_{i} \parallel}^{2}} + \lambda ΝΝ(x)\\\\= {argmin}_{x}\frac{1}{2}{\sum{\parallel Ax - {\overset{\sim}{k}}_{i} \parallel}^{2}} + \lambda ΝΝ(x)\tag{1}$$ $$$x$$$ is the target image, $$$\mathcal{F}$$$ is Fourier transform, $$$M$$$ is sampling mask, $$$S_{i}$$$ is sensitivity map of $$$i^{th}$$$ coil, $$${\overset{\sim}{k}}_{i}$$$ is the measured signal of $$$i^{th}$$$ coil, $$$NN$$$ is a neural network, $$$A$$$ is the linear forward operator.
E2E-VarNet2 solves equation (1) with an iterative gradient descent method in k-space. $$k^{t + 1} = k^{t} - ~\eta M\left( {k^{t} - \overset{\sim}{k}} \right) - G\left( k^{t} \right)~\tag{2}$$ where $$G\left( k^{t} \right) = \mathcal{F} \circ Ε \circ NN\left( \mathfrak{R} \circ \mathcal{F}^{- 1}\left( k^{t} \right) \right)\tag{3}$$ $$Ε(x) = \left( {x_{1},\cdots,x_{K}} \right) = \left( {S_{1}x,\cdots,S_{K}x} \right)\tag{4}$$ $$\mathfrak{R}\left( {x_{1},\cdots,x_{K}} \right) = {\sum_{i = 1}^{K}{S_{i}^{*}x_{i}}}\tag{5}$$ $$$G$$$ is the image space regularization network, $$$Ε$$$ is an expand operator, $$$\mathfrak{R}$$$ is a reduce operator, $$$K$$$ is the coil number.
Equation (2) represents an iterative end-to-end k-space learning network. To learn the k-space residual in an end-to-end manner, now we define: $$k = \overset{\sim}{k} + \varepsilon~\tag{6}$$ where $$$\varepsilon$$$ is the k-space residual between target k-space and acquired under-sampled k-space.Substituting equation (6) into equation (2) gives an iterative residual learning equation: $$\varepsilon^{t + 1} = ~\varepsilon^{t} - ~\eta M\varepsilon^{t} - \mathcal{F} \circ Ε \circ NN\left( {\mathfrak{R} \circ \mathcal{F}^{- 1}\left( {\overset{\sim}{k} + \varepsilon^{t}} \right)} \right)\tag{7}$$ Equation (6) & (7) represents a model based, end-to-end, k-space residual learning VarNet. Instead of passing k-space through cascades, the k-space residual is passed through all cascades and added to acquired under-sampled k-space before final image reconstruction. The corresponding model architecture is shown in figure 1.
- Residual initializer: It computes an initial k-space residual $$$\varepsilon^{0}$$$ , in our study, $$$Ax = \overset{\sim}{k}$$$ is firstly solved to get $$$x^{0}$$$ by conjugate gradient with 5 iterations, then $$$\varepsilon^{0}$$$ is calculated using equation (8) $$\varepsilon^{0} = A\left( x^{0} \right) - \overset{\sim}{k}\tag{8}$$
- Coil sensitivity estimation: Coil sensitivity map is jointly estimated with the target image through a neural network the same as E2E-VarNet.
- ISR: Image space deep learning regularization module, the backbone network is a 4-layer U-Net. Before fed into the network, k-space residual is added to the acquired k-space, then transformed to coil combined image. After the image is refined by neural network, it is expanded to multi-coil k-spaces with coil sensitivity map.
- DC: Data consistency module, which simply applies sampling mask to k-space residual $$$\varepsilon^{t}$$$.
- Output: After the end-to-end residual connection, the output module reconstructs each coil image and combine coil images into one with root of sum square (RSS) algorithm.
Fast spin echo 2D data (T2WI, FLAIR, T1WI) are collected with two in-house 3T scanners (Vantage Titan 3T, Vantage Galan 3T, Canon Medical System Corporation, Otawara, Japan). Written informed consent were obtained from all subjects. The data are split into training (1927 slices)/validation (432 slices)/test (336 slices).
The learning ground truth images are RSS reconstructed with fully sampled k-space. 8 cascades are used in our experiments, the network weights are not shared among cascades, and the gradient descent step $$$\eta$$$ is learnable. Training loss function is structure similarity6 (SSIM).
Three acceleration factors 4x/6x/8x are trained using random under-sampling mask with Auto-Calibration Signal (ACS) ratios 0.8/0.6/0.4. All models are trained using the Adam optimizer with a learning rate of 0.0005 for 50 epochs, we observe that training loss converges well without overfitting.
E2E-VarNet is trained as baseline, and our proposed E2E-ResVarNet is trained with same sensitivity map estimation module and image refinement neural network, so their total number of trainable parameters are the same.
Results & Discussion
Table 1 shows all experiments' quantitative measures including SSIM, peak signal-to-noise ratio (PSNR) and mean square error (MSE). E2E-ResVarNet is better at all acceleration factors, which demonstrates that the end-to-end residual connection together with proper initial residual estimation can improve the reconstruction performance under the supervision of physical model.Figure 2 and Figure 3 show the sample images of 4x and 6x acceleration reconstruction. E2E-ResVarNet reconstructed images are free of artifacts on all contrast images, however unsolved artifacts can be observed on E2E-VarNet reconstructed images. Besides, some tiny structures on FLAIR images look blurrier on E2E-VarNet reconstructed images compared with E2E-ResVarNet and GT.
Figure 4 shows the sample images of 8x acceleration reconstruction. Both E2E-VarNet and E2E-ResVarNet reconstructed images are quite blurry and some tiny structures are loss. E2E-VarNet reconstructed images have stronger unsolved artifacts compared with E2E-ResVarNet.
Conclusion
We introduced end-to-end residual learning into model based variational network for under-sampled MRI reconstruction, it is demonstrated that the image quality can be improved through quantitative and visual evaluation.Acknowledgements
No acknowledgement found.References
- Liang D, Cheng J, Ke Z, Ying L. Deep MRI Reconstruction: Unrolled Optimization Algorithms Meet Neural Networks. 2019:1-10. arXiv:1907.11711
- Sriram A, Zbontar J, Murrell T, et al. End-to-end variational networks for accelerated MRI reconstruction. In International Conference on Medical Image Computing and Computer-Assisted Intervention, 2020.
- Aggarwal HK, Mani MP, Jacob M. MoDL: Model-Based Deep Learning Architecture for Inverse Problems. IEEE Trans Med Imaging. 2019;38(2):394-405.
- Hammernik K, Schlemper J, Qin C, Duan J, Summers RM, Rueckert D. Systematic evaluation of iterative deep neural networks for fast parallel MRI reconstruction with sensitivity-weighted coil combination. Magn Reson Med. 2021;86(4):1859-1872
- Wang S, Cheng H, Ying L, et al. DeepcomplexMRI: Exploiting deep residual network for fast parallel MR imaging with complex convolution. Magn Reson Imaging. 2020;68(January):136-147.
- Wang Z, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: From error visibility to structural similarity. IEEE Trans Image Process. 2004;13(4):600-612.
Figures
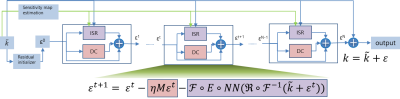
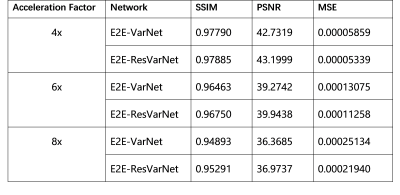
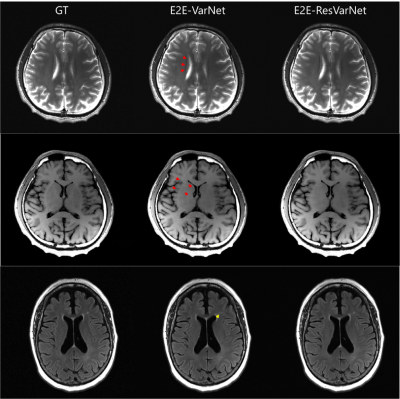
Figure 2 4x inferred result comparison (top row is T2WI, middle row is T1WI, bottom row is FLAIR). Residual artifacts (red arrow) are observed on T2WI and T1WI images of E2E-VarNet reconstruction. On FLAIR image, a region of hyper-intensity (yellow arrow) looks much blurrier compared with E2E-ResVarNet and GT.
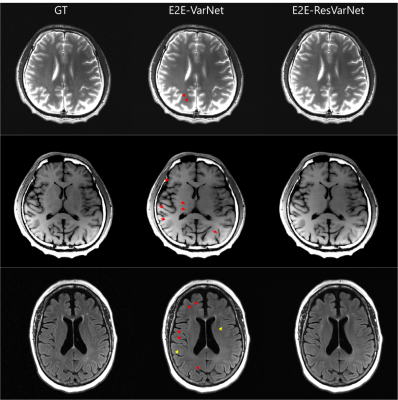
Figure 3 6x inferred result comparison (top row is T2WI, middle row is T1WI, bottom row is FLAIR). More residual artifacts (red arrows) appear on E2E-VarNet reconstructed images, especially on T1WI and FLAIR images, E2E-ResVarNet reconstructed images are free of artifacts. On FLAIR images, yellow arrow pointed structure looks blurrier on E2E-VarNet reconstructed images compared with E2E-ResVarNet and GT.
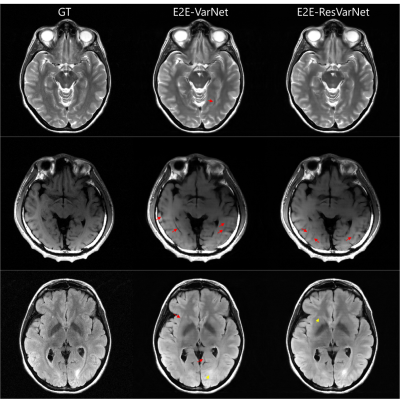
Figure 4 8x inferred result comparison (top row is T2WI, middle row is T1WI, bottom row is FLAIR). Both E2E-VarNet and E2E-ResVarNet reconstructed images are quite blurry, especially T1WI. E2E-VarNet images have stronger artifacts (red arrow). Yellow arrows point to area that is blurrier compared to the contrary reconstruction method.