Synopsis

Keywords: Machine Learning/Artificial Intelligence, Image Reconstruction, diffusion models, compressed sensing, MRI

Recovering MR images from partially acquired k-space data can reduce scan time, leading to significant applications. Deep learning approaches have been proposed to train neural networks using under-sampled and full-sampled image pairs in a supervised manner. However, these supervised models usually have poor generalizability when deployed to acquisitions different from the training datasets. Here, we propose an unsupervised Denoising Diffusion Probabilistic Model (DDPM) capable of not only generating random high-fidelity MR images but also reconstructing images corresponding to k-space data from arbitrary acquisition patterns.

Introduction

In recent years MRI has become widely adopted in hospitals and clinics. However, MRI acquisition takes a long time. Acquiring part of K-space data can reduce scan time, however leading to aliasing artefacts. Significant effort has been made to reconstruct aliasing-free images from sub-sampled k-space. Conventional algorithms, such as compressed sensing, incorporate manually crafted prior information, such as image sparsity, and use transformations such as TV and Wavelet to regularize the reconstruction results. However, these simple assumptions are generally insufficient to represent the complex data distribution and can lead to sub-optimal results, e.g., over-smoothing or residual artefacts. Deep learning approaches have been proposed to train neural networks using under-sampled K-sapce and full-sampled image pairs in a supervised manner^4,5,6. However, these supervised models usually have poor generalizability when deployed to acquisitions different from the training datasets². The Denoising Diffusion Probabilistic Model¹ (DDPM) attracts interest in the machine learning community because its sampling quality beats GAN³ and it has solid mathematical foundations. Here, we propose to train a DDPM with brain MRI images to estimate the complex data distribution (prior), and then sample the data distribution in a controlled manner guided by the actual sub-sampled k-space measurements² (posterior). Random brain MR images were generated. Different k-space acquisitions of various undersampling patterns and acceleration rates (up to 16x) were also tested.

Methods

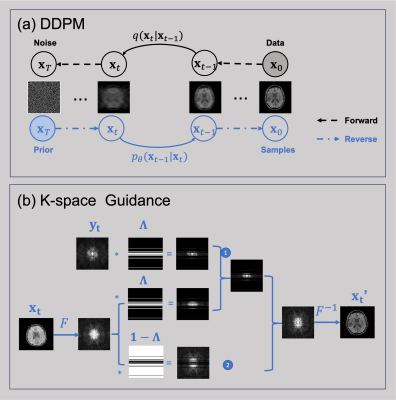
Denoising Diffusion Probabilistic Model (DDPM):

As illustrated in Fig. 1a, we can perturb brain images to noise (i.e., diffusion) by gradually adding Gaussian noise during the forward process. Define MR brain image distribution as $$$\boldsymbol{x}_{0}\sim q(\boldsymbol{x}_{0})$$$, then the perturb process that transforms the image $$$\boldsymbol{x}_{0}$$$ to noise $$$\boldsymbol{x}_{T}$$$ can be described as a Markovian process:$$q(\boldsymbol{x}_{t}|\boldsymbol{x}_{t-1})=\mathcal{N}(\boldsymbol{x}_{t};\sqrt{1-\beta_{t}}\boldsymbol{x}_{t-1},\beta_{t}^2\boldsymbol{I}), \qquad 1\leq t \leq T$$where we choose the $$$\beta_{t}$$$ schedule increase over time so that $$$\boldsymbol{x}_{T}$$$ approximates $$$\mathcal{N}(\boldsymbol{0},\boldsymbol{I})$$$.The DDPM aims to learn the reverse process that converts noise images to brain images (i.e., denoising) by optimizing a simplified objective function:$$L_{\text{simple}}=\mathbb{E}_{t\sim[1,T],\boldsymbol{x}_{0}\sim q(\boldsymbol{x}_{0}),\boldsymbol{\epsilon}\sim\mathcal{N}(\boldsymbol{0},\boldsymbol{I})}\left[\|\boldsymbol{\epsilon}-\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_{t},t)\|^{2}\right]$$where $$$\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_{t};t)$$$ represents the neural network model that can predict noise at each step. Once we trained the model $$$\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_{t};t)$$$, we can use it to eliminate noise from images gradually, and finally get brain MR images. Each sampling step can be written as:$$\boldsymbol{x}_{t-1}=a(\boldsymbol{x}_{t}-b\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_{t};t))+c\boldsymbol{\epsilon}$$ where $$$\boldsymbol{\epsilon}\sim\mathcal{N}(\boldsymbol{0},\boldsymbol{I})$$$ and $$$a,b,c$$$ are scalar parameters depending on $$$\beta$$$.
During the sampling process (i.e., image generation), we first sample a noise image $$$\boldsymbol{x}_{T}$$$ from $$$\mathcal{N}(\boldsymbol{0},\boldsymbol{I})$$$, and then use the above formula to get an image $$$\boldsymbol{x}_{0}$$$ after traversing backwards from $$$t=T$$$ to $$$t=1$$$. Since this denoising process is not controlled by any conditions (e.g., k-space measurements), the generated images correspond to random brain MR image samples from $$$q(\boldsymbol{x}_{0})$$$.

K-space measurement as a guide:

To generate brain images corresponding to the actual MRI measurement (i.e., k-space) instead of random brain images, we apply a data fidelity correction step after each denoising step to guide the direction of the generative process, as illustrated in Fig. 1b.Let $$$\boldsymbol{F}$$$ to represent the Fourier transform from image space to k-space, and $$$\boldsymbol{F}^{-1}$$$ represents the inverse. The fully k-space $$$\boldsymbol{y}_0$$$ can be modelled as:$$\boldsymbol{y}_0=\boldsymbol{F}\boldsymbol{x}_0+\boldsymbol{\epsilon}$$where $$$\boldsymbol{\epsilon}\sim\mathcal{N}(\boldsymbol{0},\boldsymbol{I})$$$ represents the Gaussian noise during signal acquisition. Similarly, we can easily perturb the k-space by $$$\boldsymbol{y}_t=\sqrt{1-\beta_{t}}\boldsymbol{y}_0+\sqrt{\beta_{t}}\boldsymbol{F}\boldsymbol{\epsilon}$$$ at each sampling step, and then add an extra step to use the perturbed $$$\boldsymbol{y}_t$$$ to guide image generation process:$$\boldsymbol{x}_{t}'=\boldsymbol{F}^{-1}\underset{\text{1}}{[\underbrace{\lambda\boldsymbol{\Lambda}\boldsymbol{y}_{t}+(1-\lambda)\boldsymbol{\Lambda}\boldsymbol{F}\boldsymbol{x}_{t}}}+\underset{2}{\underbrace{(\boldsymbol{I}-\boldsymbol{\Lambda})\boldsymbol{F}\boldsymbol{x}_{t}}}]$$where $$$\boldsymbol{\Lambda}$$$ represents the subsampling mask. In the formula, part 1 describes the mixture of $$$\boldsymbol{y}_t$$$ and $$$\boldsymbol{x}_t$$$ on the masked k-space region with $$$\lambda$$$ as the mixture weight, balancing data fidelity and image prior. Part 2 is the reconstruction from the unmasked k-space region. The modified $$$\boldsymbol{x}_t'$$$ will be fed forward to the next denoising step.

Experiments

We trained the diffusion model using a brain MRI dataset with 130k gradient-echo magnitude images (2D axial, 8 echoes from 4 ms to 30 ms) from 300 subjects. Each image is resized to 128x128 (2mm in-plane resolution) to fit in GPU memory. We implement this model with a U-Net of depth 32 and trained this model in A100 GPU with 40G memory for 2 days. The number of steps was set to 1000. It takes about 2 mins to sample a batch of 4 images on the same GPU.

Results

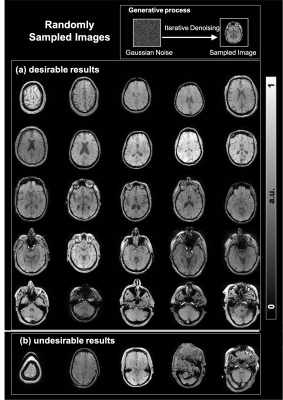
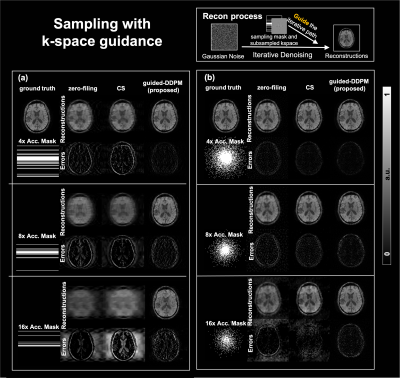
Fig. 2 shows randomly generated brain images (a) 25 random brain images that appear realistic and diverse. (b) 5 examples of randomly generated images that appear artifactual with distorted brain shapes.

Fig. 3 shows the undersampling reconstruction results of different acceleration factors (4, 8, and 16) for 1D and 2D masks. Compared with the zero-filling and the compressed-sensing results, our DDPM results led to superior performance, particularly for high acceleration rates.

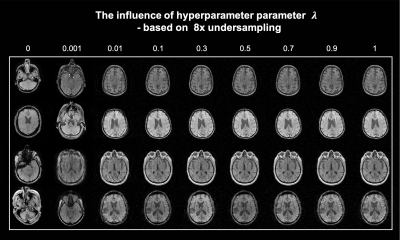
Fig. 4 demonstrates the k-space guidance effect on image generation by setting different weighting factors λ, which indicates the influence strength of K-space measurement. The whole generative process can be correctly guided with a relatively small λ.

Conclusion

We have proposed a k-space measurements guided diffusion model that can synthesize high-quality MRI images corresponding to actual MRI acquisitions. This k-space guidance generative approach is a new promising method that eliminates the need for pair training data. Furthermore, without retraining the model, it can reconstruct high-fidelity MR images from highly accelerated acquisitions of arbitrary undersampling patterns.

Acknowledgements

HS received funding from Australian Research Council (DE210101297).