0388
Database-Free Zero-Shot Deep Learning Reconstruction for Highly-Accelerated Free-Breathing Perfusion CMR1Electrical and Computer Engineering, University of Minnesota, Minneapolis, MN, United States, 2Center for Magnetic Resonance Research, University of Minnesota, Minneapolis, MN, United States, 3Department of Medicine (Cardiology), University of Minnesota, Minneapolis, MN, United States, 4Delft University of Technology, Delft, Netherlands, 5Department of Radiology, Mayo Clinical, Rochester, MN, United States
Synopsis
Keywords: Machine Learning/Artificial Intelligence, Machine Learning/Artificial Intelligence
Myocardial perfusion CMR is used to functionally assess coronary artery disease. However, its resolution and coverage remain limited and require rapid imaging .At high accelerations for whole-heart coverage and high spatio-temporal resolution, conventional reconstructions suffer from noise and aliasing artifacts. Physics-guided deep learning (PG-DL) reconstruction has shown improved image quality in fast MRI, but its application to perfusion CMR has been limited due to substantial differences in breathing and contrast uptakes among subjects. In this work, we tackle these challenges by adopting subject-specific self-supervised PG-DL that does not require a training database for simultaneous multi-slice accelerated myocardial perfusion CMR.INTRODUCTION
First-pass perfusion cardiac MRI (CMR) is commonly used for functional assessment of coronary artery disease1. Due to the use of snap-shot imaging during the passage of a contrast agent, its resolution and coverage remain limited despite numerous advances in accelerated MRI, including simultaneous multi-slice (SMS) imaging2,3 and compressed sensing4-6 at higher acceleration rates. Recently, physics-guided deep learning (PG-DL) has enabled higher acceleration rates in MRI, where conventional methods suffer from noise and residual artifacts7,8. Yet, its use in perfusion CMR has been limited, due to difficulties of curating high-quality databases, especially due to substantial differences of time-varying physiological processes such as breathing or contrast uptakes across subjects9. In this work, we tackle these challenges and improve myocardial perfusion CMR using subject-specific zero-shot PG-DL10 that does not require a training database or reference images. Results show the proposed method improves on conventional methods, as well as a recent database-trained PG-DL strategy.METHODS
Imaging Experiments:Free-breathing first-pass myocardial perfusion CMR was acquired on 3T in 6 subjects. Simultaneous multi-slice (SMS)=3 and uniform Cartesian in-plane acceleration=4 (no ACS) was used. A saturation-prepared GRE sequence with slab-selective outer volume suppression11 was used with the following imaging parameters: FOV=360×320mm2, resolution=1.7×1.7mm2, temporal resolution=116ms and slice-thickness=8mm. Non-prepared GRE calibration scans at a lower resolution acquired with resolution=1.7×5.6mm2.
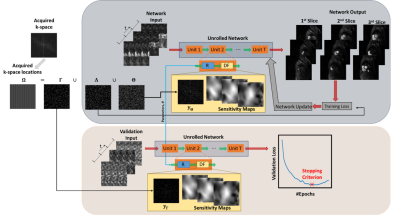
Zero-Shot PG-DL Reconstruction for SMS:
Regularized SMS reconstruction solves:
$$\mathbf{x}^{\mathrm{SMS}}=\arg \min _{\mathbf{x}^{ \mathrm{SMS}}}\left\|\mathbf{y}_{\Omega}^{\mathrm{SMS}}-\mathbf{E}_{\Omega}^{\mathrm{SMS}} \mathbf{x}^{\mathrm{SMS}}\right\|_2^2+{\mathscr R}\left(\mathbf{x}^{\mathrm{SMS}}\right), \quad\quad\quad (1)$$
where $$$\mathbf{y}_{\Omega}^{\mathrm{SMS}}$$$ is the acquired SMS k-space, Ω is the in-plane undersampling pattern, $$$\mathbf{E}_{\Omega}^{\mathrm{SMS}}$$$ is the multi-coil encoding operator, $$$\mathbf{x}^{\mathrm{SMS}}$$$ is the image of slices concatenated in readout dimension9,12 and $$${\mathscr R}$$$ is a regularizer. In PG-DL, algorithm unrolling is used to solve this problem13. These networks alternate between data-fidelity and proximal operators, which are handled by linear methods and implicitly via neural networks respectively14. Though supervised learning remains popular, it requires a reference dataset; and for perfusion CMR, this reference is typically generated by a surrogate method such as compressed sensing15-17. Alternatively, self-supervised learning (SSDU) has been proposed to enable training of PG-DL networks without reference data, and has been applied to CMR applications18, including perfusion9.
Zero-shot learning10 builds on SSDU, and splits the acquired indices Ω to three disjoint as $$$\Omega = \Theta \cup \Lambda \cup \Gamma$$$. $$$\Theta$$$ enforces data-fidelity in the PG-DL network; $$$\Lambda$$$, which is unseen by the network, is used to define k-space loss, while $$$\Gamma$$$ is to define a k-space validation loss to determine early stopping and avoid overfitting (Fig. 1)10. ZS-SSDU loss, with a multi-mask data augmentation strategy19 is given as:
$$\min _{\boldsymbol{\theta}} \frac{1}{K} \sum_{\mathrm{k}=1}^K {\mathscr L}\left(\mathbf{y}_{\Lambda_{\mathrm{k}}}^{\mathrm{SMS}}, \mathbf{E}_{\Lambda_{\mathrm{k}}}^{\mathrm{SMS}}\left({\mathscr f}\left(\mathrm{y}_{\Theta_{\mathrm{k}}}^{\mathrm{SMS}}, \mathbf{E}_{\Theta_{\mathrm{k}}}^{\mathrm{SMS}} ; \boldsymbol{\theta}\right)\right)\right), \quad\quad\quad (2)$$
where $$${\mathscr L}(\cdot,\cdot)$$$ is the training loss, $$${\mathscr f}(\cdot,\cdot)$$$ denotes the network output, K is the number of masks and $$$\boldsymbol{\theta}$$$ denotes the network parameters. The k-space self-validation loss is calculated at jth epoch from the learned network weights specified by $$$\boldsymbol{\theta}^{(j)}$$$ via:
$${\mathscr L}\left(\mathbf{y}_{\Gamma}, \mathbf{E}_{\Gamma}\left({\mathscr f}\left(\mathbf{y}_{\Omega \backslash \Gamma}, \mathbf{E}_{\Omega \backslash \Gamma} ; \boldsymbol{\theta}^{(j)}\right)\right)\right). \quad\quad\quad (3)$$
PG-DL Implementation Details:
A 3D unrolled PG-DL network was used in ZS-SDDU10, where subject-specific regularization was performed across all time-frames (Fig. 1) on two test subjects separately. A 3D ResNet14 was used for the regularizer, with all 40 time-frames as inputs, and 256 channels in its hidden layers. Data-fidelity was solved using conjugate gradient for 10 iterations with sensitivity maps generated by ESPIRiT20 from the separate calibration scan. Adam optimizer was used with LR=$$$5\cdot10^{-4}$$$ and mixed normalized $$$\ell_1-\ell_2$$$ loss for 100 epochs. 20% of $$$\Omega$$$ was uniformly randomly selected for $$$\Gamma$$$.
Comparisons were made to split slice-GRAPPA (SP-SG)21, locally-low rank (LLR) regularized reconstruction22 and a PG-DL database training using signal intensity informed multi-coil (SIIM) encoding operator for the data-fidelity9. The latter was trained on 420 distinct k-spaces from 4 subjects using Adam optimizer, learning rate=$$$3\cdot10^{-4}$$$, 100 epochs and normalized ℓ1-ℓ2 loss.
Images were assessed by an experienced reader on a 4-point scale (1:best, 4:worst) for aliasing artifacts, SNR, blurring and overall quality.
RESULTS
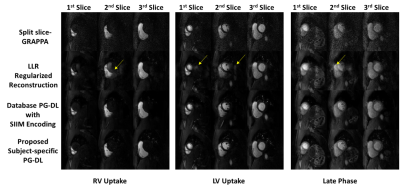
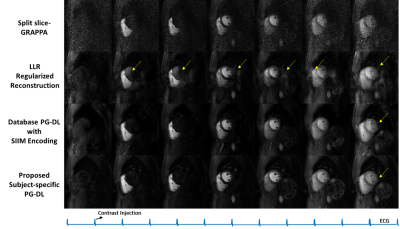
Fig. 2 shows reconstructed slices from an SMS slice group for LV uptake, RV uptake and a late-phase. SP-SG suffers from heavy noise amplification. LLR reconstruction reduce noise but with residual aliasing artifacts. Database PG-DL with SIIM encoding eliminates aliasing and reduces noise, though noise in later time-frames with lower SNR is visible. The proposed zero-shot PG-DL shows no aliasing and the least amount of noise throughout the acquisition.Fig. 3 depicts reconstruction of a slice across various time-frames from another subject. Similar observations apply, with the proposed zero-shot PG-DL approach improving on database-trained PG-DL with visually better image quality in the later time-frames.
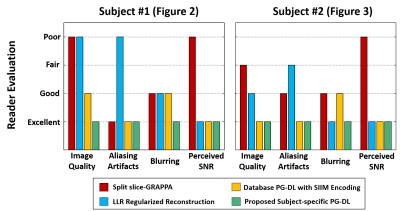
Fig. 4 summarizes the image assessment results, where the proposed approach was scored excellent in all categories, and outperformed all other methods. SP-SG was scored worst in perceived SNR, while LLR reconstruction was scored worst in aliasing artifacts. Database-trained PG-DL had worse scores than proposed zero-shot PG-DL in terms of overall image quality and blurring.
DISCUSSION AND CONCLUSIONS
In this study, we proposed database-free zero-shot PG-DL reconstruction, trained in a subject-specific manner for highly-accelerated perfusion CMR. Proposed approach improved on conventional methods, as well as database-trained PG-DL, showing superior image quality, as confirmed by reader evaluation.Acknowledgements
Funding: Grant support: NIH R01HL153146, NIH P41EB027061, NIH R21EB028369, NSFCCF-1651825. NWO STU.019.024, 4TU Federation and AHA Predoctoral Fellowship.References
[1] R. Franks, C. Amedeo and P. Sven , "Clinical application of dynamic contrast enhanced perfusion imaging by cardiovascular magnetic resonance." Frontiers in Cardiovascular Medicine (2021).
[2] Y. Yang, et al. "Whole‐heart spiral simultaneous multi‐slice first‐pass myocardial perfusion imaging." Magnetic Resonance in Medicine 81.2 (2019): 852-862.
[3] M.S. Nazir, et al. "Simultaneous multi slice (SMS) balanced steady state free precession first-pass myocardial perfusion cardiovascular magnetic resonance with iterative reconstruction at 1.5 T." J Cardiovasc Magn Reason, 20.1 (2018): 1-11.
[4] Yang Y, Kramer CM, Shaw PW, Meyer CH, Salerno M. First-pass myocardial perfusion imaging with whole-heart coverage using L1-SPIRiT accelerated variable density spiral trajectories. Magn Reson Med. 2016;76:1375-1387.
[5] Shin T, Nayak KS, Santos JM, Nishimura DG, Hu BS, McConnell MV. Three-dimensional first-pass myocardial perfusion MRI using a stack-of-spirals acquisition. Magn Reson Med. 2013;69:839-844.
[6] Iyer SK, Tasdizen T, Likhite D, DiBella E. Split Bregman multicoil accelerated reconstruction technique: a new framework for rapid reconstruction of cardiac perfusion MRI. Med Phys. 2016;43:1969-1981.
[7] K. Hammernik, T. Klatzer, et al., “Learning a variational network for reconstruction of accelerated MRI data,” Magn Reson Med, vol. 79, pp. 3055–3071, 2018.
[8] J. Schlemper, J. Caballero, J. V. Hajnal, A. N. Price, and D. Rueckert, “A deep cascade of convolutional neural networks for dynamic MR image reconstruction,” IEEE Trans Med Imaging, vol. 37, no. 2, pp. 491–503, 2017.
[9] Demirel, Omer Burak, et al. "Signal intensity informed multi‐coil encoding operator for physics‐guided deep learning reconstruction of highly accelerated myocardial perfusion CMR." Magnetic resonance in medicine (2022).
[10] Yaman, Burhaneddin, et al. "Zero-Shot Self-Supervised Learning for MRI Reconstruction." ICLR, 2022.
[11] S. Weingärtner, S. Moeller, and M. Akçakaya, “Feasibility of ultra-high simultaneous multi-slice and in-plane accelerations for cardiac MRI using outer volume suppression and leakage-blocking reconstruction,” in Proc ISMRM, 2018
[12] Demirel, Omer Burak, et al. "Improved simultaneous multislice cardiac MRI using readout concatenated k‐space SPIRiT (ROCK‐SPIRiT)." Magnetic resonance in medicine 85.6 (2021): 3036-3048
[13] Aggarwal HK, Mani MP, Jacob M. MoDL: Model-based deep learning architecture for inverse problems. IEEE Trans Med Imaging. 2019; 38: 394- 405.
[14] Yaman, Burhaneddin, et al. "Self‐supervised learning of physics‐guided reconstruction neural networks without fully sampled reference data." Magnetic Resonance in Medicine 84.6 (2020): 3172-3191.
[15] Wang JY, Weller DS, Kramer CM, Salerno M. DEep learning-based rapid spiral image REconstruction (DESIRE) for high-resolution spiral first-pass myocardial perfusion imaging. NMR Biomed. 2022;35:e4661.
[16] Le J, Tian Y, Mendes J, et al. Deep learning for radial SMS myocardial perfusion reconstruction using the 3D residual booster U-net. Magn Reson Imaging. 2021;83:178-188.
[17] Fan LXZ, Shen DM, Haji-Valizadeh H, et al. Rapid dealiasing of undersampled, non-Cartesian cardiac perfusion images using U-net. NMR Biomed. 2020;33:e4239.
[18] Yaman, Burhaneddin, et al. "Self-supervised physics-guided deep learning reconstruction for high-resolution 3d LGE CMR." 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI). IEEE, 2021.
[19] Yaman, Burhaneddin, et al. "Multi‐mask self‐supervised learning for physics‐guided neural networks in highly accelerated magnetic resonance imaging." NMR in Biomedicine (2022): e4798.
[20] M. Uecker, P. Lai, et al., “ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA,” Magn Reson Med, vol. 71, no. 3, pp. 990–1001, 2014.
[21] S. F. Cauley, J. R. Polimeni, H. Bhat, L. L. Wald, and K. Setsompop, “Interslice leakage artifact reduction technique for simultaneous multislice acquisitions,” Magn Reson Med, vol. 72, no. 1, pp. 93–102, 2014.
[22] Miao, Xin, et al. "Accelerated cardiac cine MRI using locally low rank and finite difference constraints." Magnetic resonance imaging 34.6 (2016): 707-714.
Figures